【计算机视觉】使用仿射变换将一幅图像放置到另一幅图像中
一、涉及函数及原理:
1、Haffine_from_points函数
计算单应性矩阵H,仿射变换,使得tp是fp经过仿射变换H得到的。该函数会返回给定对应点对的最优仿射变换。该函数是使用对应点对来计算过仿射变换矩阵。
- 仿射变换
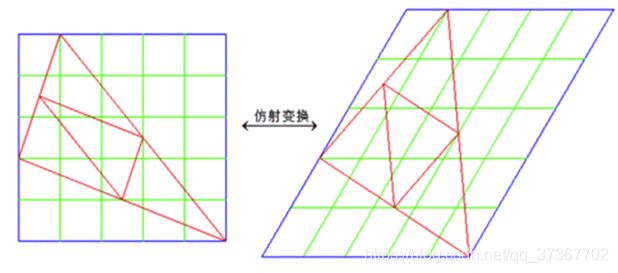
仿射变换属于单应性变换,单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换。仿射变换就是允许图像任意伸缩的变换,可以保持原来的线共点,点共线的关系不变,保持原来相互平行的线仍然平行,保持原来的中点仍然是中点,保持原来在一直线上几段线段之间的比例关系不变。但是仿射变换不能保持原来的线段长度不变,也不能保持原来的夹角角度不变。如下图:
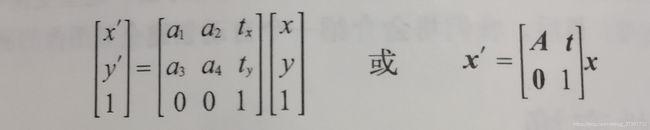
仿射变换包含一个可逆矩阵A和一个平移向量t=[tx,ty]。
Haffine_from_points函数代码:
from pylab import *
def Haffime_from_points(fp,tp):
if fp.shape !=tp.shape:
raise RuntimeError('number of point do not match')
#对点进行归一化
#映射起始点
m = mean(fp[:2],axis=1)
maxstd=max(std(fp[:2],axis=1))+1e-9
C1 = diag([1 / maxstd, 1 / maxstd, 1])
C1[0][2]=-m[0]/maxstd
C1[1][2] = -m[1] / maxstd
fp_cond=dot(C1,fp)
#映射对应点
m = mean(tp[:2], axis=1)
C2 = C1.copy() # must use same scaling for both point sets
C2[0][2] = -m[0] / maxstd
C2[1][2] = -m[1] / maxstd
tp_cond = dot(C2, tp)
# 因为归一化后点的均值为0,所以平移量为0
A = concatenate((fp_cond[:2], tp_cond[:2]), axis=0)
U, S, V = linalg.svd(A.T)
# 创建矩阵B和C
tmp = V[:2].T
B = tmp[:2]
C = tmp[2:4]
tmp2 = concatenate((dot(C, linalg.pinv(B)), zeros((2, 1))), axis=1)
H = vstack((tmp2, [0, 0, 1]))
# 反归一化
H = dot(linalg.inv(C2), dot(H, C1))
return H / H[2, 2]
2、image_in_image函数
使用仿射变换将im1放置在im2上,使im1图像的角和tp尽可能的靠近,这边tp是齐次坐标来表示的,并且按照从左上角逆时针计算的。输入参数为两幅图像和一个坐标。该坐标为将第一幅图像放置到第二幅图像的角点坐标(这边的坐标使用齐次坐标下的坐标表示)
- alpha 通道
Alpha Channel是指一张图片的透明和半透明度。添加透明度,即需要在RGB三个通道的基础上添加alpha通道信息。
本次实验中创建的alpha图像定义了每个像素从各个图像中获取的像素值成分多少。扭曲的图像是在扭曲区域边界之外以0来填充的图像,来创建一个二值的alpha图像。alpha值=0时为透明,alpha值=1时为不透明。
二、运行代码及结果分析
1、实现代码:
from pylab import *
from PIL import Image
import warp
im1 = array(Image.open('01.jpg').convert('L'))
im2 = array(Image.open('02.jpg').convert('L'))
im3 = array(Image.open('lei.jpg').convert('L'))
tp = array([[20,520,620,20],[100,50,600,600],[1,1,1,1]])
tp1 = array([[1100,1300,1300,1100],[1500,1500,1700,1700],[1,1,1,1]])
im4 = warp.image_in_image(im1,im2,tp)
im5 = warp.image_in_image(im3,im4,tp1)
figure()
gray()
imshow(im5)
axis('off')
show()2、运行效果图
(嵌入了两张图像,图像位置大小可通过调整坐标来修改)