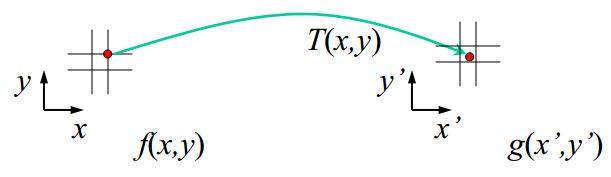使用仿射变换将一幅图像放置到另一幅图像中

一，原理分析

       仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次二维坐标到二维坐标的线性变换。仿射变换可以来表示:旋转 (线性变换)，平移 (向量加)，缩放操作 (线性变换)，仿射变换代表的是两幅图之间的位置关系。

      在本案例中，实现了仿射变换的简单例子，即将一幅图像放置到另一幅图像中，使其能够和指定区域或标记物对齐。

      1.读取两张图像，分别将两张图像的每个像素的位置坐标，以矩阵的形式存储在数组中。然后插入到第二张图像的指定位置，即目标点。

这些目标点的坐标值可通过查看绘制的图像（在pylab图像中，鼠标的坐标显示在图像底部附近）手工确定的。

      2.调用warp.py的image_in_image()函数，获取要变换的第一幅图像的角点坐标

     3.调用homography.py的Haffine_from_points(tp,fp)函数，计算仿射变换矩阵，使得tp是fp经过仿射变换H得到的。以平移为例，H就是那个平移量，原始坐标(x,y)，通过(x+H,y+H)得到的就是变换后的图像坐标点。

     4.调用Scipy工具包中的ndimage包进行扭曲操作，对图像块进行仿射变换。ndimage.affine_transform(im1,H[:2,:2],
                    (H[0,2],H[1,2]),im2.shape[:2])，对应的第一个参数为要处理的图片，参数二为线性变换的尺度，参数三为平移向量，参数四为支付那个输出图像的大小。

     5. 将扭曲的图像和第二幅图像融合，创建alpha图像。扭曲区域边界之外以0来填充图像，然后通过计算(1-alpha)*im2 + alpha*im1_t  ，处理这些像素，得到最后的变换图像。

二，代码

 # -*- coding: utf-8 -*-
from PCV.geometry import warp, homography
from PIL import  Image
from pylab import *
from scipy import ndimage

# 将im1仿射扭曲到im2的指定位置
im1 = array(Image.open('b_meitu_2.jpg').convert('L'))
im2 = array(Image.open('a_meitu_1.jpg').convert('L'))
# 选定指定的位置，即目标点
tp = array([[324,442,448,324],[453,453,272,270],[1,1,1,1]])
#调用的warp.py的image_in_image函数，从而实现仿射变换
im3 = warp.image_in_image(im1,im2,tp)
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)
axis('off')
show()

# -*- coding: cp936 -*-
import matplotlib.delaunay as md 
from scipy import ndimage
from pylab import *
from numpy import *

from PCV.geometry import homography
    

def image_in_image(im1,im2,tp):
   # 使用仿射变换将im1放置在im2上，使im1图像的四个坐标角点与tp尽可能靠近，
#tp为将第一幅图像放置到第二幅图像中的角点坐标，且是从左上角逆时针的 
    
    # 扭曲的点
    m,n = im1.shape[:2]  # 读取矩阵的行和列，即图像一的长和宽
    fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]]) #标记要变换的第一幅图像im1的角点坐标
    
    # 计算仿射变换，并且将其应用于图像im1
    H = homography.Haffine_from_points(tp,fp)#计算H，仿射变换，使得tp是fp经过仿射变换H得到的
    im1_t = ndimage.affine_transform(im1,H[:2,:2],  # 使用Scipy工具包中的ndimage包进行扭曲操作，对图像块进行仿射变换
                    (H[0,2],H[1,2]),im2.shape[:2])  
    alpha = (im1_t > 0)                             # 创建alpha图像，扭曲边界以外的用0来填充图像，以内就是扭曲图像的像素
    
    return (1-alpha)*im2 + alpha*im1_t              # 最后计算得到仿射变换后的图像

def Haffine_from_points(fp,tp):
#计算H，仿射变换，使得tp和fp经过仿射变换H得到
    
    if fp.shape != tp.shape:
        raise RuntimeError('number of points do not match')
        
    # 对点进行归一化
    # --映射起始点--
    m = mean(fp[:2], axis=1)
    maxstd = max(std(fp[:2], axis=1)) + 1e-9
    C1 = diag([1/maxstd, 1/maxstd, 1]) 
    C1[0][2] = -m[0]/maxstd
    C1[1][2] = -m[1]/maxstd
    fp_cond = dot(C1,fp)
    
    # --映射对应点--
    m = mean(tp[:2], axis=1)
    C2 = C1.copy() #两个点集，必须都进行相同的缩放
    C2[0][2] = -m[0]/maxstd
    C2[1][2] = -m[1]/maxstd
    tp_cond = dot(C2,tp)
    
    # 因为归一化后的点均值为0，所以平移量为0
    A = concatenate((fp_cond[:2],tp_cond[:2]), axis=0)
    U,S,V = linalg.svd(A.T)
    
    # 创建矩阵B和C
    tmp = V[:2].T
    B = tmp[:2]
    C = tmp[2:4]
    
    tmp2 = concatenate((dot(C,linalg.pinv(B)),zeros((2,1))), axis=1) 
    H = vstack((tmp2,[0,0,1]))
    
    # 反归一化
    H = dot(linalg.inv(C2),dot(H,C1))
    
    return H / H[2,2]

三，运行结果

以下图片均拍摄于集美大学