基于Python的K邻近分类法（KNN）+ 稠密SIFT + 手势识别

一、KNN原理分析

       在分类方法中，最简单也用的最多的就是KNN（K邻近分类法）算法。这种算法把要分类的对象与训练集中，已知类标记的所有对象进行对比，并由k近邻对指派到哪一类进行投票。

       这种方法通常分类效果很好，但也有很多弊端，例如：与K-menas聚类算法类似，需要预先设定k值，k值的选择会影响分类的性能。而且，这种方法要求整个训练集存储起来，如果训练集非常大时，就会出现搜索速度慢的现象。

二、用K邻近分类器分类二维数据

1、创建二维点集

       通过随机生成的方式，创建两个不同的二维点集，每个点集有两类，分别是正态分布和绕环状分布，然后用Pickle模块保存数据集。二维点集的大小主要通过代码中参数的调节实现，该参数越大，数据点范围越大，就会比较分散。

数据在绕环状分布时，半径r决定了外圈数据集的集中程度，当r越大时，数据范围越大，也就越分散。

# -*- coding: utf-8 -*-
from numpy.random import randn
import pickle
from pylab import *

#创建二维样本数据
n = 200
# 两个正态分布数据集
class_1 = 1 * randn(n,2)
class_2 = 1.5 * randn(n,2) + array([5,1])
labels = hstack((ones(n),-ones(n)))

# 用Pickle模块保存
#with open('points_normal.pkl', 'w') as f:
with open('points_normal_test.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
    
# 正太分布，并使数据成环绕状分布
print ("save OK!")
class_1 = 0.3 * randn(n,2)
r = 0.5 * randn(n,1) + 5
angle = 2*pi * randn(n,1)
class_2 = hstack((r*cos(angle),r*sin(angle)))
labels = hstack((ones(n),-ones(n)))

# 用Pickle保存
#with open('points_ring.pkl', 'w') as f:
with open('points_ring_test.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
    
print ("save OK!")

保存成功后，在控制台输出如下：

2、创建KNN分类器

用Pickle模块载入之前创建的数据集，从而来创建一个KNN分类器模型。为可视化所有测试数据点的分类，并展示分类器如何将两个不同的类分开，就需要创建一个辅助函数classify(x,y,model=model)，以获取x和y二维坐标数组和分类器，并且返回一个预测的类标记数组array。然后把函数classify作为参数传递给实际的绘图函数plot_2D_boundary。

这个绘图函数需要一个决策函数（分类器），并且用meshgrid()函数在一个网格上进行预测，网格的精度为0.1，每隔0.1采集一个点。决策函数的等值线可以显示边界的位置，默认边界为零等值线。对于每一个类，用*画出分类正确的类，用O画出分类不正确的点。

# -*- coding: utf-8 -*-
import pickle
from pylab import *
from PCV.classifiers import knn
from PCV.tools import imtools

pklist=['points_normal.pkl','points_ring.pkl']

figure()

# 用Pickle载入二维数据点
for i, pklfile in enumerate(pklist):
    with open(pklfile, 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)
    # 用Pickle模块载入测试数据
    with open(pklfile[:-4]+'_test.pkl', 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)

    model = knn.KnnClassifier(labels,vstack((class_1,class_2)))
    
    # 在测试数据集的第一个数据点上进行测试
    print (model.classify(class_1[0]))

    # 定义绘图函数
    def classify(x,y,model=model):
        return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])

    # 绘制分类边界
    subplot(1,2,i+1)
    imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
    titlename=pklfile[:-4]
    title(titlename)
show()

imtools函数： 

def plot_2D_boundary(plot_range,points,decisionfcn,labels,values=[0]):
    """    Plot_range为(xmin,xmax,ymin,ymax), points是类数据点列表, decisionfcn is a funtion to evaluate, 
        是评估函数，labels是函数 decisionfcn 关于每一个类返回值的标记列表. """
        
    clist = ['b','r','g','k','m','y'] # 不同的类用不同的颜色标识
    
    # 在一个网格上进行评估，并画出决策函数的边界
    x = arange(plot_range[0],plot_range[1],.1)
    y = arange(plot_range[2],plot_range[3],.1)
    xx,yy = meshgrid(x,y)
    xxx,yyy = xx.flatten(),yy.flatten() # 网格中的x,y坐标点列表
    zz = array(decisionfcn(xxx,yyy)) 
    zz = zz.reshape(xx.shape)
    # 以values画出边界
    contour(xx,yy,zz,values) 
        
    # 对于每类，用 '*' 画出分类正确的点,用 'o'画出分类不正确的点
    for i in range(len(points)):
        d = decisionfcn(points[i][:,0],points[i][:,1])
        correct_ndx = labels[i]==d
        incorrect_ndx = labels[i]!=d
        plot(points[i][correct_ndx,0],points[i][correct_ndx,1],'*',color=clist[i])
        plot(points[i][incorrect_ndx,0],points[i][incorrect_ndx,1],'o',color=clist[i])
    
    axis('equal')

3、结果分析

（1）改变正态分布数据集的参数

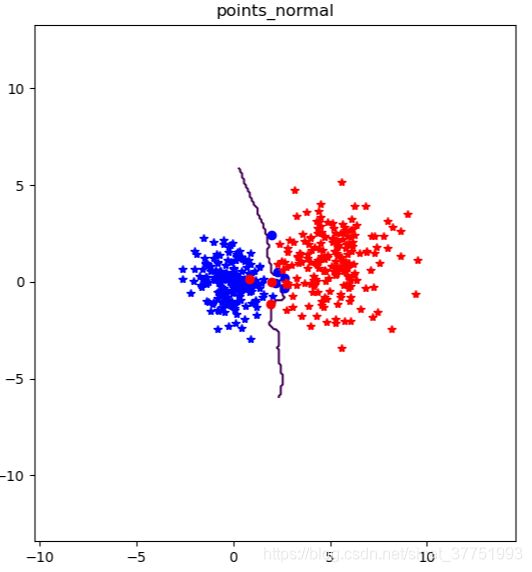
修改参数前的数据集进行分类

结果如下：

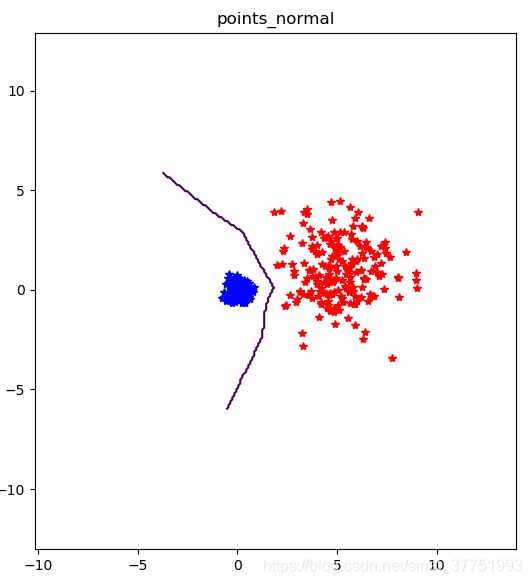
调节参数后

  

分类结果如下：

分析：通过比较左侧的图看出，修改参数之前的数据集下，由于两个数据集的范围都比较大，就有可能出现了相同的数据点，给分类造成了干扰，无法进行分类，从而用原点标记出这几个错误的点。而在修改参数后的数据集下，两个数据集的范围相差较大，从而产生的数据点相差的比较大， 从而分类器能够较好的进行分类。

（2）改变环绕状数据集的参数

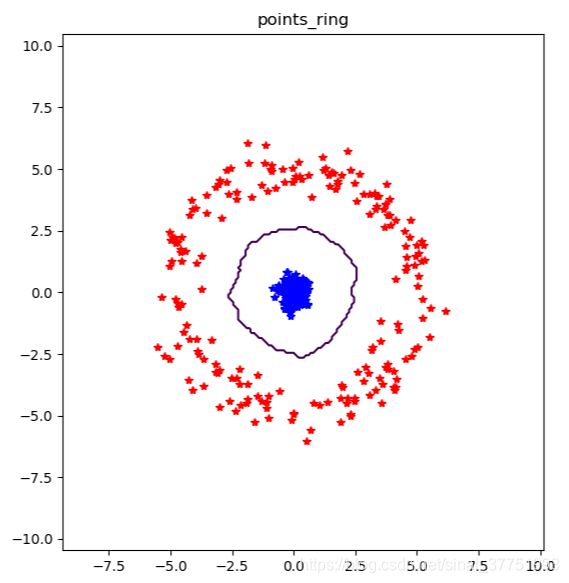
修改参数前的数据集进行分类

结果如下：

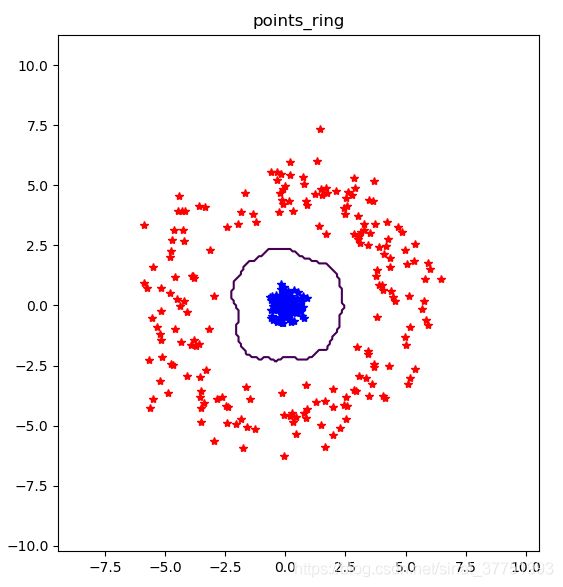
修改参数后的数据集进行分类

结果如下：

分析：由于半径变大，从而使外圈的数据集更加分散，从而更加靠近中间的内圈的数据集

二、Dense SIFT

1、原理分析

       Dense-SIFT是sift的密集采样板，由于SIFT的实时性差，目前特征提取多采用密集采样。传统的SIFT算法即Sparse SIFT，不能很好地表征不同类之间的特征差异，达不到所需的分类要求。而Dense SIFT算法，是一种对输入图像进行分块处理，再进行SIFT运算的特征提取过程。Dense SIFT根据可调的参数大小，来适当满足不同分类任务下对图像的特征表征能力。通常来讲Dense SIFT更适用于图像分类识别的任务，而Sparse SIFT更适用于图像检索分割的任务。

2、可视化

# -*- coding: utf-8 -*-
from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

dsift.process_image_dsift('gesture/b1.jpg','b1.dsift',90,60,True)
l,d = sift.read_features_from_file('b1.dsift')
im = array(Image.open('gesture/b1.jpg'))
sift.plot_features(im,l,True)
title('dense SIFT')
show()

 dsift函数：

from PIL import Image
from numpy import *
import os

from PCV.localdescriptors import sift


def process_image_dsift(imagename,resultname,size=20,steps=10,force_orientation=False,resize=None):
    """ 用密集采样的SIFT描述子处理一幅图像，并将结果保存在一个文件中.
         可选的输入：特征的大小size，位置之间的步长steps，
         是否强迫计算描述子的方位force_orientation(False表示所有的方位都是朝上的），
         用于调整图像大小的元组"""

    im = Image.open(imagename).convert('L')
    if resize!=None:
        im = im.resize(resize)
    m,n = im.size
    
    if imagename[-3:] != 'pgm':
        #创建一个人pgm文件
        im.save('tmp.pgm')
        imagename = 'tmp.pgm'

    # 创建帧，并保存到临时文件
    scale = size/3.0
    x,y = meshgrid(range(steps,m,steps),range(steps,n,steps))
    xx,yy = x.flatten(),y.flatten()
    frame = array([xx,yy,scale*ones(xx.shape[0]),zeros(xx.shape[0])])
    savetxt('tmp.frame',frame.T,fmt='%03.3f')
    
    path = os.path.abspath(os.path.join(os.path.dirname("__file__"),os.path.pardir))
    path = path + "\\python3-ch08\\win32vlfeat\\sift.exe "
    if force_orientation:
        cmmd = str(path+imagename+" --output="+resultname+
                    " --read-frames=tmp.frame --orientations")
    else:
        cmmd = str(path+imagename+" --output="+resultname+
                    " --read-frames=tmp.frame")
    os.system(cmmd)
    print ('processed', imagename, 'to', resultname)

当 dsift.process_image_dsift('gesture/b1.jpg','b1.dsift',90,60,True)时，结果如下：

当  dsift.process_image_dsift('gesture/b1.jpg','b1.dsift',90,40,True)时，结果如下：

通过两幅图像的对比可以看出，当圈的大小确定时，步数越小，相邻圆圈中心点的距离就越近，整体看起来也就越密

 

三、手势识别

       在这个应用中，我们用稠密SIFT描述子来表示这些手势图像，并建立一个简单的手势识别系统。代码会对指定的图像创建一个特征文件，文件名后缀为.dsitf。

       注意！！！ 这里将测试的所有图像，分辨率全部调成常见的固定大小，例如：50*50,。这是非常重要的，否则这些图像会有不同数量的描述子，从而每幅图像的特征向量长度也不一样，这将导致在后面比较它们时出错。

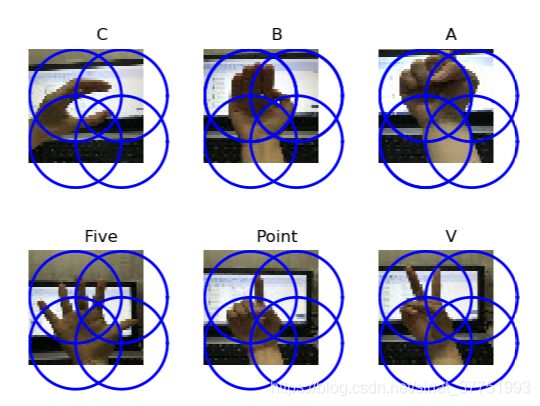
1、可视化带有描述子的手势图像

# -*- coding: utf-8 -*-
import os
from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

imlist=['gesture/test2/C-uniform06.jpg','gesture/test2/B-uniform04.jpg',
        'gesture/test2/A-uniform02.jpg','gesture/test2/Five-uniform08.jpg',
        'gesture/test2/Point-uniform10.jpg','gesture/test2/V-uniform12.jpg']

figure()
for i, im in enumerate(imlist):
    print (im)
    dsift.process_image_dsift(im,im[:-3]+'dsift',60,20,True)
    l,d = sift.read_features_from_file(im[:-3]+'dsift')
    dirpath, filename=os.path.split(im)
    im = array(Image.open(im))
    #显示手势含义title
    titlename=filename[:-14]
    subplot(2,3,i+1)
    sift.plot_features(im,l,True)
    title(titlename)
show()

 

 

2、通过训练数据，识别手势

      用训练数据及其标记作为输入，创建分类器对象，然后在整个测试集上遍历，并用classify（）方法对每一幅图像进行分类。将布尔数组和1相乘并求和，可以计算出分类的正确率。

      虽然正确率显示了对于给定的测试集有多少图像是正确分类的，但是它并没有告诉我们哪些手势难以分类，或者犯哪些错误。这时，我们可以通过混淆矩阵来显示错误分类的情况。混淆矩阵是一个可以显示每类有多少个样本被分在每一类中的矩阵，它可以显示错误的分布情况，以及哪些类是经常相互“混淆”的

# -*- coding: utf-8 -*-
from PCV.localdescriptors import dsift
import os
from PCV.localdescriptors import sift
from pylab import *
from PCV.classifiers import knn

def get_imagelist(path):
    """    Returns a list of filenames for
        all jpg images in a directory. """

    return [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.jpg')]

def read_gesture_features_labels(path):
    # 对所有以 .dsift为后缀的文件创建一个列表
    featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
    # 读取特征
    features = []
    for featfile in featlist:
        l,d = sift.read_features_from_file(featfile)
        features.append(d.flatten())
    features = array(features)
    # 创建标签
    labels = [featfile.split('/')[-1][0] for featfile in featlist]
    return features,array(labels)

def print_confusion(res,labels,classnames):
    n = len(classnames)
    # 混淆矩阵
    class_ind = dict([(classnames[i],i) for i in range(n)])
    confuse = zeros((n,n))
    for i in range(len(test_labels)):
        confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
    print ('Confusion matrix for')
    print (classnames)
    print (confuse)

filelist_train = get_imagelist('gesture/train2')
filelist_test = get_imagelist('gesture/test2')
imlist=filelist_train+filelist_test

# 将图像尺寸调成(50,50)，然后进行处理
for filename in imlist:
    featfile = filename[:-3]+'dsift'
    #dsift.process_image_dsift(filename,featfile,10,5,resize=(50,50))

features,labels = read_gesture_features_labels('gesture/train2/')
test_features,test_labels = read_gesture_features_labels('gesture/test2/')
classnames = unique(labels)

# 测试kNN
k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in
range(len(test_labels))])
# 准确率
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print ('Accuracy:', acc)

print_confusion(res,test_labels,classnames)

knn函数

from numpy import * 

class KnnClassifier(object):
    
    def __init__(self,labels,samples):
        """ Initialize classifier with training data. """
        
        self.labels = labels
        self.samples = samples
    
    def classify(self,point,k=3):
        """ Classify a point against k nearest 
            in the training data, return label. """
        
        # compute distance to all training points
        dist = array([L2dist(point,s) for s in self.samples])
        
        # sort them
        ndx = dist.argsort()
        
        # use dictionary to store the k nearest
        votes = {}
        for i in range(k):
            label = self.labels[ndx[i]]
            votes.setdefault(label,0)
            votes[label] += 1
            
        return max(votes, key=lambda x: votes.get(x))


def L2dist(p1,p2):
    return sqrt( sum( (p1-p2)**2) )


def L1dist(v1,v2):
    return sum(abs(v1-v2))

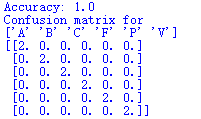
（1）训练集与测试集完全相同时：

准确率为100%

识别出，每种手势各有两种，与静态数据库中一致。

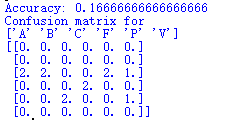
（2）训练集与测试集完全不同时：

准确率只有16%

很多手势出现了分类的错误，例如：A手势识别成了C手势，B手势也识别成了C手势等

大量的分类错误，可能的原因有：1、在静态数据库下，对陌生场景下的手势，比较敏感，导致准确率较低

                                                      2、训练集较小，导致分类错误

四、解决问题

1、注意将代码中读取图像的格式，改成你们测试图像相应的后缀

 2、在dsift函数中，路径要改成你们存储图像的相对路径，否则会导致.dsift文件无法生成