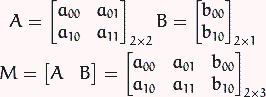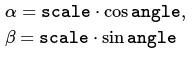基于OpenCV的图像几何变换小结 (仿射变换为主)
参考:https://blog.csdn.net/keith_bb/article/details/56331356
图片位移
可手写代码实现矩阵搬移操作。
也可使用仿射变换方法进行操作:
例如,仿射矩阵可写为:
[[1 0 100]
[0 1 200]] ,即表示x位移100,y位移200像素点。
图片缩放
1、放大、缩小,使用cv.resize(src,(new,newH))
2、常用的插值算法如下:
i.最近邻域插值:选最近的点复制即可。
ii.双线性插值:
首先计算A1、A2、B1、B2 。然后计算目标点(可根据A1 、A2计算,也可根据B1、B2计算)
图片仿射
1、图片仿射变换(位移+旋转+缩放):
仿射变换是指在向量空间中进行一次线性变换(乘以一个矩阵)并加上一个平移(加上一个向量),变换为另一个向量空间的过程。在有限维的情况下,每个仿射变换可以由一个矩阵A和一个向量b给出,它可以写作A和一个附加的列b。一个仿射变换对应于一个矩阵和一个向量的乘法,而仿射变换的复合对应于普通的矩阵乘法,只要加入一个额外的行到矩阵的底下,这一行全部是0除了最右边是一个1,而列向量的底下要加上一个1.Affine Transform描述了一种二维仿射变换的功能,它是一种二维坐标之间的线性变换,保持二维图形的“平直性”(即变换后直线还是直线,圆弧还是圆弧)和“平行性”(其实是保持二维图形间的相对位置关系不变,平行线还是平行线,而直线上的点位置顺序不变,另特别注意向量间夹角可能会发生变化)。仿射变换可以通过一系列的原子变换的复合来实现包括:平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和错切(Shear). 事实上,仿射变换代表的是两幅图之间的关系,我们通常使用2x3矩阵来表示仿射变换如下:
得到如下结果:
2.仿射变换求法
从上面解释中我们得知仿射变换表示的就是两幅图片的一种联系,关于这种联系的信息大致可以从以下两种场景获得。
a. 我们已知X和T而且我们知道他们是有联系的,接下来的工作就是求解矩阵M
b. 我们一致M和X要求得T,我们只需要应用算式T=M·X即可。对于这种联系的信息可以用矩阵M清晰的表达(即给出明确的2x3矩阵)或者也可以用两幅图片点之间几何关系来表达。
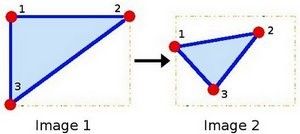
因为矩阵M联系着两幅图片,我们以其表示两图中各三点直接的联系为例,如下:
点1,2和3(在图一中形成一个三角)与图二中三个点一一映射,仍然形成三角形,但形状已经大大改变。如果我们能通过这样两组三点求出仿射变换(你能选择自己喜欢的点),接下来我们就能把仿射变换应用到图像中所有的点。
openCV中有直接根据三个边界点计算转换矩阵的函数:
M = cv.getAffineTransform(matSrc_3Point,matDst_3Point)
3.opencv实现仿射变换
利用opencv实现仿射变换一般会涉及到warpAffine和getRotationMatrix2D两个函数,其中warpAffine可以实现一些简单的重映射,而getRotationMatrix2D可以获得旋转矩阵M。
getRotationMatrix2D函数
Matcv::getRotationMatrix2D ( Point2f center,
double angle,
double scale
)
参数解释
. center:Point2f类型,表示原图像的旋转中心
. angle: double类型,表示图像旋转角度,角度为正则表示逆时针旋转,角度为负表示逆时针旋转(坐标原点是图像左上角)
. scale: 缩放系数
函数计算如下矩阵:
warpAffine函数
void cv::warpAffine ( InputArray src,
OutputArray dst,
InputArray M,
Size dsize,
int flags =INTER_LINEAR,
int borderMode =BORDER_CONSTANT,
const Scalar & borderValue = Scalar()
)
参数解释
. src: 输入图像
. dst: 输出图像,尺寸由dsize指定,图像类型与原图像一致
. M: 2X3的变换矩阵
. dsize: 指定图像输出尺寸
. flags: 插值算法标识符,有默认值INTER_LINEAR,如果插值算法为WARP_INVERSE_MAP, warpAffine函数使用如下矩阵进行图像转换
示例代码
#include
#include
#include
#include
using namespace std;
using namespace cv;
//全局变量
String src_windowName = "原图像";
String warp_windowName = "仿射变换";
String warp_rotate_windowName = "仿射旋转变换";
String rotate_windowName = "图像旋转";
int main()
{
Point2f srcTri[3];
Point2f dstTri[3];
Mat rot_mat(2, 3, CV_32FC1);
Mat warp_mat(2, 3, CV_32FC1);
Mat srcImage, warp_dstImage, warp_rotate_dstImage, rotate_dstImage;
//加载图像
srcImage = imread("D://timg.jpg");
//判断文件是否加载成功
if (srcImage.empty())
{
cout << "图像加载失败!" << endl;
return -1;
}
else
cout << "图像加载成功!" << endl << endl;
//创建仿射变换目标图像与原图像尺寸类型相同
warp_dstImage = Mat::zeros(srcImage.rows, srcImage.cols, srcImage.type());
//设置三个点来计算仿射变换
srcTri[0] = Point2f(0, 0);
srcTri[1] = Point2f(srcImage.cols - 1, 0);
srcTri[2] = Point2f(0, srcImage.rows - 1);
dstTri[0] = Point2f(srcImage.cols*0.0, srcImage.rows*0.33);
dstTri[1] = Point2f(srcImage.cols*0.85, srcImage.rows*0.25);
dstTri[2] = Point2f(srcImage.cols*0.15, srcImage.rows*0.7);
//计算仿射变换矩阵
warp_mat = getAffineTransform(srcTri, dstTri);
//对加载图形进行仿射变换操作
warpAffine(srcImage, warp_dstImage, warp_mat, warp_dstImage.size());
//计算图像中点顺时针旋转50度,缩放因子为0.6的旋转矩阵
Point center = Point(warp_dstImage.cols / 2, warp_dstImage.rows / 2);
double angle = -50.0;
double scale = 0.6;
//计算旋转矩阵
rot_mat = getRotationMatrix2D(center, angle, scale);
//旋转已扭曲图像
warpAffine(warp_dstImage, warp_rotate_dstImage, rot_mat, warp_dstImage.size());
//将原图像旋转
warpAffine(srcImage, rotate_dstImage, rot_mat, srcImage.size());
//保存结果图像
cv::imwrite("D://仿射后图像.jpg", warp_dstImage);
cv::imwrite("D://仿射后旋转图像.jpg", warp_rotate_dstImage);
cv::imwrite("D://原图像旋转图像.jpg", rotate_dstImage);
//显示变换结果
namedWindow(src_windowName, WINDOW_AUTOSIZE);
imshow(src_windowName, srcImage);
namedWindow(warp_windowName, WINDOW_AUTOSIZE);
imshow(warp_windowName, warp_dstImage);
namedWindow(warp_rotate_windowName, WINDOW_AUTOSIZE);
imshow(warp_rotate_windowName, warp_rotate_dstImage);
namedWindow(rotate_windowName, WINDOW_AUTOSIZE);
imshow(rotate_windowName, rotate_dstImage);
waitKey(0);
return 0;
} 原图:
仿射变换后图像:
仿射变换后旋转图像:
原图像旋转后图像: