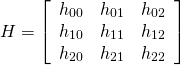仿射变换——图像到图像
一,单应性变换
单应性变换就是一个平面到另一个平面的映射关系。
如图,两张图片中相同颜色的点叫做corresponding Points,比如两个红点就是一对corresponding points。单应性矩阵(Homography)就是一个从一张图像到另一张图像映射关系的转换矩阵(3*3)。可以由下面的公式来表示:
以图像中的红点为例,可以将单应性变换写成如下形式:
二,仿射变换
它相当于一个平移变换和一个非均匀变换的复合,用A矩阵表示,A为3×3矩阵,A={{a11,a12,tx},{a21,a22,ty},{0,0,1}} 其中A可以分解为:A=R(a)R(-b)DR(b),其中D={{c1,0},{0,c2}}左上角2×2矩阵为旋转部分,tx和ty为平移因子,它有6个自由度,即旋转4个,x方向平移,y方向平移。他能保持平行性,不能保持垂直性,Image中各部分变换前后面积比保持不变,共线线段或者平行线段的长度比保持不变,矢量的线性组合不变。面积被缩放了c1*c2=detA倍。
仿射变换主要包括平移变换、旋转变换、缩放变换(也叫尺度变换)、倾斜变换(也叫错切变换、剪切变换、偏移变换)、翻转变换,有六个自由度。
仿射变换的特点:
仿射变换保持二维图形的“平直性”和“平行性”,但是角度会改变。
“平直性”:变换后直线还是直线、圆弧还是圆弧。
“平行性”:平行线还是平行线,直线上点的位置顺序不变。
它有6个自由度,即旋转4个,也就是前述大矩形的4个元素都可以同时改变,x方向平移,y方向平移。它能保持平行性,不能保持垂直性,Image中各部分变换前后面积比保持不变,共线线段或者平行线段的长度比保持不变,矢量的线性组合不变。
三,alpha通道(图像通道)
Alpha通道是一个单独通道,相当于一个关联表一样的东西,来定义这个像素点的透明度的属性,当只有它这一张图的时候不会有什么作用,但是当将有透明度的图片和其他的图片进行叠加的时候,透明度就能够产生它的作用了。如果一张透明的图片,则阿尔法的作用之就是0,在叠加的时候,这块区域上的图片之后又本来的颜色,而不会有它自己的颜色。alpha的作用位1的时候,就是将图片覆盖在了这块区域上。
实现代码:
# -*- coding: utf-8 -*-
from PCV.geometry import warp, homography
from PIL import Image
from pylab import *
from scipy import ndimage
# example of affine warp of im1 onto im2
im1 = array(Image.open('D:/img/logo.png').convert('L'))
im2 = array(Image.open('D:/img/jmu.jpg').convert('L'))
# set to points
tp = array([[88,180,180,88],[40,36,605,605],[1,1,1,1]])
#tp = array([[675,826,826,677],[55,52,281,277],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)
# set from points to corners of im1
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# first triangle
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# compute H
H = homography.Haffine_from_points(tp2,fp2)#返回给定对应点的最优仿射变换
im1_t = ndimage.affine_transform(im1,H[:2,:2],#扭曲
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])#三角形的alpha图像
im3 = (1-alpha)*im2 + alpha*im1_t
# second triangle
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()实验结果:
参考:
https://blog.csdn.net/chaolei3/article/details/79531140
https://blog.csdn.net/algzjh/article/details/80152230