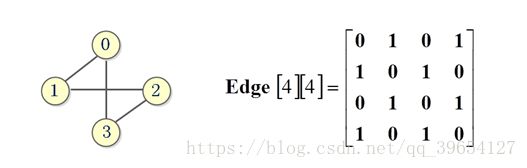图的定义与存储结构(邻接矩阵、邻接链表)
目录
1、图的定义与操作
2、图的存储结构
1、图的邻接矩阵结构
2、图的邻接链表结构
3、时间复杂度的对比分析
1、图的定义与操作
定义
-图是由顶点集合( Vertex ) 及顶点间的关系集合( Edge )组成的一种数据结构: Graph= (V, E)
V = { x | x ∈ 某个数据对象 } 是顶点的有穷非空集合
E = { (x, y) | x , y ∈ V }是顶点之间关系(边)的有穷集合
思考: G1, G2, G3, G4都是图吗?有什么异同?可以继续分类吗?
都是由有穷顶点集与边集组成的,所以都是图
链表是特殊的二叉树,二叉树是特殊的图
无向边
-顶点 x 和 y 之间的边没有方向,则称该边为无向边
- (x , y) 与 (y , x) 意义相同,表示 x 和 y 之间有连接
无向图
-图中任意两个顶点之间的边均是无向边,则称该图为无向图
有向边
-顶点 x 和 y 之间的边有方向,则称该边为有向边
-
●
●
有向图
- 图中任意两个顶点之间的边均是有向边,则称该图为有向图
无向图可以看作一种特殊的有向图!(所以后续代码只考虑有向图)
顶点邻接( Adjacent )的定义
-对于无向图 :如果 (x, y) ∈ E , 则称顶点 x 和 y 互为邻接
-对于有向图 :如果
度( Degree )的定义
-顶点 v 的度是和 v 相关联的边的数目,记为 TD(v)
● 入度:以 v 为头的边的数目,记为 ID(v)
● 出度:以 v 为尾的边的数目,记为 OD(v)
推论
-TD(v) = ID(v) + OD(v)
-Count(E) = ID(v1) + ID(v2) +…+ ID(vn)
-Count(E) = OD(v1) + OD(v2) +…+ OD(vn)
-Count(E) = [ TD(v1) + TD(v2) +…+ TD(vn) ] / 2 (由前三项易推导)
权( Weight )的定义
-与图的边相关的数据元素叫做权
-权常用来表示图中顶点间的距离或者耗费
图的一些常用操作
-设置顶点的值
-获取顶点的值
-获取邻接顶点
-设置边的值
-删除边
-获取顶点数
-获取边数
- 。。。
图在程序中表现为一种特殊的数据类型
编程实验
图抽象类的创建 Graph.h
#ifndef GRAPH_H
#define GRAPH_H
#include "Object.h"
#include "SharedPointer.h"
#include "Array.h"
namespace DTLib
{
// V:与顶点相关联数据元素类型,E:与边相关联数据元素(权值)类型
template < typename V, typename E >
class Graph : public Object
{
public:
/* 获取顶点相关联数据元素值 */
virtual V getVertex(int i) = 0;
virtual bool getVertex(int i, V& value) = 0;
/* 设置顶点相关联数据元素值 */
virtual bool setVertex(int i, const V& value) = 0;
/* 获取邻接顶点 */
virtual SharedPointer< Array > getAdjacent(int i) = 0;
/* 判断在当前图中顶点i到顶点j是否邻接 */
virtual bool isAdjacent(int i, int j) = 0;
/* 获取边相关联数据元素值 */
virtual E getEdge(int i, int j) = 0;
virtual bool getEdge(int i, int j,E& value) = 0;
/* 设置边相关联数据元素值 */
virtual bool setEdge(int i, int j, const E& value) = 0;
/* 删除边 */
virtual bool removeEdge(int i, int j) = 0;
/* 顶点数 */
virtual int vCount() = 0;
/* 边数 */
virtual int eCount() = 0;
/* 出度 */
virtual int OD(int i) = 0;
/* 入度 */
virtual int ID(int i) = 0;
/* 度 */
virtual int TD(int i)
{
return ID(i) + OD(i);
}
/* 判断当前的有向图是否能够看做无向图 */
bool asUndirected()
{
bool ret = true;
for(int i=0; i main.cpp
#include
#include "Graph.h"
using namespace std;
using namespace DTLib;
int main()
{
Graph* g = NULL;
return 0;
}
小结
图是顶点与边的集合,是一种非线性的数据结构
图中顶点可以与多个其它顶点产生邻接关系
图中的边有与之对应的权值,表示顶点间的距离
图在程序中表现为特殊的数据类型
2、图的存储结构
1、图的邻接矩阵结构
基本思想
-用一维数组存储顶点:描述顶点相关的数据
-用二维数组存储边:描述顶点间的关系和权
邻接矩阵法
-用二维数组表示顶点间关系(边、权值)
-设图 A = (V, E) 是一个有 n 个顶点的图,图的邻接矩阵为 Edge[n] [n] , 则:
i 和 j 代表顶点编号,若矩阵某一个值不为空就代表一个权值
注:解决工程问题时,习惯于对图中的每个顶点进行编号
当不需要权值时,取W非空表示结点间有连接
邻接矩阵法示例
-无向图的邻接矩阵是对称的
-有向图的邻接矩阵可能是不对称的
设计与实现
实现的关键在于存储顶点集和边集
问题: 如何具体表示顶点集数组? 如何具体表示边集数组?
实现方式一
-直接使用数组表示顶点集和边集 (不推荐)
//N : 图中顶点的个数 V : 与顶点关联数据元素类型 E : 权值类型
template < int N, typename V, typename E >
class MatrixGraph : public Graph
{
protected:
V m_vertexes[N]; // 与顶点相关联数据元素
E m_edges[N][N]; // 邻接矩阵
int m_eCount; // 图的边数
public:
// ...
};
分析下面代码的效率
struct TV
{
int a1[100];
char a2[1000];
TV()
{
/* init array */
}
};
struct TE
{
float a1[100];
long a2[1000];
TE()
{
/* init array */
}
};
int main()
{
MatrixGraph<1000, TV, TE> g;
return 0;
}
问题
-构造效率低下
☹ 图对象初始化时,频繁调用顶点类型和边类型的构造函数
-空间使用率低下
☹ 图对象占用大量空间,而大多数空间处于闲置状态
-无法表示空值
☹ 无法用统一的方式表示边为空的情形
实现方式二
-使用指针数组表示顶点集和边集
//N : 图中顶点的个数 V : 与顶点关联数据元素类型 E : 权值类型
template < int N, typename V, typename E >
class MatrixGraph : public Graph
{
protected:
V* m_vertexes[N]; // 每一个成员指向与顶点相关联数据元素
E* m_edges[N][N];
int m_eCount;
public:
// ...
};
问题的解决
-构造效率
☺ 初始化图对象时,只需要将数组元素赋值为空
-空间使用率
☺ 顶点数据元素和边数据元素在需要时动态创建
-空值的表示
☺ 任意的顶点类型和边类型都使用NULL表示空值
编程实验
图的邻接矩阵结构 class MatrixGraph
#ifndef MATRIXGRAPH_H
#define MATRIXGRAPH_H
#include "Graph.h"
#include "Exception.h"
#include "DynamicArray.h"
namespace DTLib
{
//N : 图中顶点的个数 V : 与顶点关联数据元素类型 E : 权值类型
template < int N, typename V, typename E >
class MatrixGraph : public Graph
{
protected:
V* m_vertexes[N]; // 每一个成员指向与顶点相关联数据元素
E* m_edges[N][N]; // 邻接矩阵
int m_eCount; // 当前图的边数
public:
MatrixGraph()
{
for(int i=0; i > getAdjacent(int i)
{
DynamicArray* ret = NULL;
if( (0 <= i) && (i < vCount()) )
{
int n = 0;
for(int j=0; j(n); // 用数组存放邻接顶点编号
if(ret != NULL)
{
for(int j=0, k=0; jset(k++, j);
}
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object ...");
}
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ...");
}
return ret;
}
/* 获取顶点i,j间边权值 */
E getEdge(int i, int j)
{
E ret;
if( !getEdge(i, j, ret) )
{
THROW_EXCEPTION(InvalidParameterException, "Index is invalid ...");
}
return ret;
}
bool getEdge(int i, int j, E& value) //O(1)
{
bool ret =( (0 <= i) && (i < vCount()) &&
(0 <= j) && (j < vCount()) );
if( ret )
{
if(m_edges[i][j] != NULL) // 有权值
{
value = *(m_edges[i][j]);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No value assigned to this edge ...");
}
}
return ret;
}
bool setEdge(int i, int j, const E& value)
{
bool ret = (0 <= i) && (i < vCount()) &&
(0 <= j) && (j < vCount());
if( ret )
{
E* ne = m_edges[i][j];
if(m_edges[i][j] == NULL) // 没有权值(边)
{
ne = new E();
if( ne )
{
*ne = value;
m_edges[i][j] = ne;
m_eCount++;
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory store new edge ...");
}
}
else
{
*ne = value;
}
}
return ret;
}
bool removeEdge(int i, int j) //O(1)
{
bool ret = (0 <= i) && (i < vCount()) &&
(0 <= j) && (j < vCount());
if( ret )
{
E* toDel = m_edges[i][j];
m_edges[i][j] = NULL;
if(toDel != NULL)
{
m_eCount--;
delete toDel;
}
}
return ret;
}
int vCount()
{
return N;
}
int eCount()
{
return m_eCount;
}
// 顶点i的出度,i为尾,
int OD(int i)
{
int ret = 0;
if( (0 <= i) && (i < vCount()) )
{
for(int j=0; j
int ID(int i)
{
int ret = 0;
if( (0 <= i) && (i < vCount()) )
{
for(int j=0; j main.cpp
#include
#include "MatrixGraph.h"
using namespace std;
using namespace DTLib;
int main()
{
MatrixGraph<3, int, int> g;
g.setEdge(0, 1, 1);
g.setEdge(1, 0, 2);
g.setEdge(1, 2, 3);
cout << "vCount : " << g.vCount() << endl;
cout << "eCount : " << g.eCount() << endl;
cout << "ID(1) : " << g.ID(1) << endl;
cout << "OD(1) : " << g.OD(1) << endl;
cout << "TD(1) : " << g.TD(1) << endl;
cout << "W(0,1) : " << g.getEdge(0, 1) << endl;
cout << "W(1,0) : " << g.getEdge(1, 0) << endl;
cout << "W(1,2) : " << g.getEdge(1, 2) << endl;
SharedPointer< Array > aj = g.getAdjacent(1);
for(int i=0; ilength(); i++)
{
cout << (*aj)[i] << " ";
}
cout << "Delete Edge : " < 小结
邻接矩阵法使用数组对图相关的数据进行存储
一维数组存储顶点相关的数据(空表示无相关数据)
二维数组存储边相关的数据(空表示顶点间无连接)
代码实现时使用指针数组进行数据的存储(提高效率)
2、图的邻接链表结构
邻接矩阵法中的残留问题
-MatrixGraph 无法动态添加/删除顶点,一旦指定结点数,就无法改变了
-当 N = 1000, 邻接矩阵的体积为 4 * 1000 * 1000 字节;因此图对象创建后即使不存在任何连接对象也要占用4M空间
基本思想
-为了进一步提离空间使用率,可以考虑使用链表替换数组,将邻接矩阵变换为邻接链表
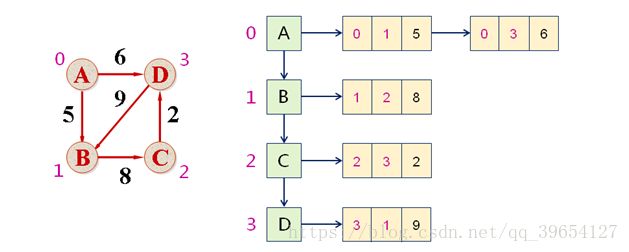
邻接链表法
-图中的所有顶点按照编号存储于同一个链表中
-每一个顶点对应一个链表,用于存储始发于该顶点的边
-每一条边的信息包含:起点,终点,权值
设计与实现
边数据类型的设计
template < typename E >
struct Edge : public Object
{
int b; // 起始顶点
int e; // 邻接顶点
E data; // 权值
// ...
};顶点数据类型的设计
struct Vertex : public Object
{
V* data;
LinkList< Edge > edge; // 当前顶点的邻接链表
// ...
};
LinkList m_list; 动态增加/删除顶点
-int addVertex();
☛ 增加新的顶点,返回顶点编号 (只能在链表末尾增加)
-int addVertex(const V& value);
☛ 增加新顶点的同时附加数据元素
-void removeVertex();
☛ 删除最近增加的顶点
编程实验
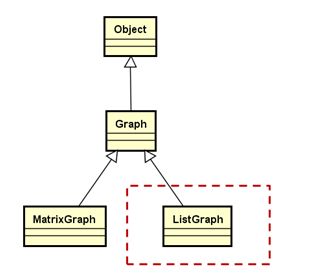
图的邻接链表结构 class ListGraph;
Graph.h
#ifndef GRAPH_H
#define GRAPH_H
#include "Object.h"
#include "SharedPointer.h"
#include "Array.h"
namespace DTLib
{
template < typename E >
struct Edge : public Object
{
int b;
int e;
E data;
Edge(int i=-1, int j=-1)
{
b = i;
e = j;
}
Edge(int i, int j, const E& value)
{
b = i;
e = j;
data = value;
}
bool operator == (const Edge& obj)
{
return (b == obj.b) && (e == obj.e);
}
bool operator != (const Edge& obj)
{
return !(*this == obj);
}
bool operator < (const Edge& obj)
{
return (data < obj.data);
}
bool operator > (const Edge& obj)
{
return (data > obj.data);
}
};
// V:与顶点相关联数据元素类型,E:与边相关联数据元素(权值)类型
template < typename V, typename E >
class Graph : public Object
{
public:
// ...
};
}
#endif // GRAPH_H
ListGraph.h
#ifndef LISTGRAPH_H
#define LISTGRAPH_H
#include "Graph.h"
#include "Exception.h"
#include "LinkList.h"
#include "DynamicArray.h"
namespace DTLib
{
template < typename V, typename E >
class ListGraph : public Graph
{
protected:
struct Vertex : public Object
{
V* data; // 顶点
LinkList< Edge > edge; // 当前顶点的邻接链表
Vertex()
{
data = NULL;
}
};
LinkList m_list;
public:
ListGraph(unsigned int n=0)
{
for(unsigned int i=0; i 0)
{
setVertex(ret, value);
}
return ret;
}
bool setVertex(int i, const V& value) // O(n)
{
bool ret = (0 <= i) && (i < vCount());
if( ret )
{
Vertex* vertex = m_list.get(i);
V* data = vertex->data;
if(data == NULL)
{
data = new V();
}
if(data != NULL)
{
*data = value;
vertex->data = data;
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new vertex object ...");
}
}
return ret;
}
bool isAdjacent(int i, int j)
{
return (0 <= i) && (i < vCount()) && (0 <= j) && (j < vCount()) && (m_list.get(i)->edge.find(Edge(i, j)) >= 0);
}
V getVertex(int i)
{
V ret;
if( !getVertex(i, ret) )
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ...");
}
return ret;
}
bool getVertex(int i, V& value) // O(n)
{
bool ret = (0 <= i) && (i < vCount());
if( ret )
{
Vertex* v = m_list.get(i);
if(v->data != NULL)
{
value = *(v->data);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No value assigned to this vertex ...");
}
}
return ret;
}
void removeVertex() // O(n^2)
{
if(m_list.length() > 0)
{
int index = m_list.length() - 1; // 删除结点编号
Vertex* v = m_list.get(index);
// 删除最近增加的顶点后,也要将关联边删除
if( m_list.remove(index) )
{
// 从第一个顶点到最后一个顶点中是否存在删除顶点关联的边
for(int i=(m_list.move(0), 0); !m_list.end(); i++, m_list.next())
{
int pos = m_list.current()->edge.find(Edge(i, index)); // 查找以i为起点index为终点的边是否存在于该顶点的邻接链表
/*
* 在find函数中有两条边对象==操作,所以在Graph中重载==操作符。
* 是否存在的标准是起点和终点(index)是否相等
*/
if(pos >= 0)
{
m_list.current()->edge.remove(pos);
}
}
delete v->data;
delete v;
}
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No vertex in current graph ...");
}
}
SharedPointer< Array > getAdjacent(int i) // O(n)
{
DynamicArray* ret = NULL;
if((0 <= i) & &(i < vCount()))
{
Vertex* vertex = m_list.get(i);
ret = new DynamicArray(vertex->edge.length());
if(ret != NULL)
{
for(int k = (vertex->edge.move(0), 0); !vertex->edge.end(); k++, vertex->edge.next())
{
ret->set(k, vertex->edge.current().e);
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object ...");
}
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ...");
}
return ret;
}
E getEdge(int i, int j)
{
E ret;
if( !getEdge(i, j, ret) )
{
THROW_EXCEPTION(InvalidParameterException, "Edge is invalid ...");
}
return ret;
}
bool getEdge(int i, int j, E& value) // O(n)
{
bool ret = ((0 <= i) && (i < vCount()) &&
(0 <= j) && (j < vCount()));
if( ret )
{
Vertex* vertex = m_list.get(i);
int pos = vertex->edge.find(Edge(i, j));
if(pos >= 0)
{
value = vertex->edge.get(pos).data;
}
else
{
THROW_EXCEPTION(InvalidOperationException,"No value assigned to this edge ...");
}
}
return ret;
}
bool setEdge(int i, int j, const E& value) // O(n)
{
bool ret = ((0 <= i) && (i < vCount()) &&
(0 <= j) && (j < vCount()));
if( ret )
{
Vertex* vertex = m_list.get(i);
int pos = vertex->edge.find(Edge(i, j));
if(pos >= 0)
{
ret = vertex->edge.set(pos, Edge(i, j, value));
}
else
{
ret = vertex->edge.insert(0, Edge(i, j, value)); // 边不存在,加条边
}
}
return ret;
}
bool removeEdge(int i, int j) //O(n)
{
bool ret = ((0 <= i) && (i < vCount()) &&
(0 <= j) && (j < vCount()));
if( ret )
{
Vertex* vertex = m_list.get(i);
int pos = vertex->edge.find(Edge(i, j));
if(pos >= 0)
{
ret = vertex->edge.remove(pos);
}
}
return ret;
}
int vCount() // O(1)
{
return m_list.length();
}
int eCount() // O(n)
{
int ret = 0;
for(m_list.move(0); !m_list.end(); m_list.next())
{
ret += m_list.current()->edge.length();
}
return ret;
}
int ID(int i) // O(n*n)
{
int ret = 0;
if((0 <= i) && (i < vCount()))
{
for(m_list.move(0); !m_list.end(); m_list.next())
{
LinkList< Edge >& edge = m_list.current()->edge;
for(edge.move(0); !edge.end(); edge.next())
{
if(edge.current().e == i)
{
ret++;
break;
}
}
}
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ...");
}
return ret;
}
int OD(int i) //O(n)
{
int ret = 0;
if((0 <= i) && (i < vCount()))
{
ret = m_list.get(i)->edge.length();
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ...");
}
return ret;
}
~ListGraph()
{
while(m_list.length() > 0)
{
Vertex* toDel = m_list.get(0);
m_list.remove(0);
delete toDel->data;
delete toDel;
}
}
};
}
#endif // LISTGRAPH_H
main.cpp
#include
#include "ListGraph.h"
using namespace std;
using namespace DTLib;
int main()
{
ListGraph g(4);
// 创建前文的图
g.setVertex(0, 'A');
g.setVertex(1, 'B');
g.setVertex(2, 'C');
g.setVertex(3, 'D');
for(int i=0; i > aj = g.getAdjacent(0);
for(int i=0; ilength(); i++)
{
cout << (*aj)[i] << endl;
}
cout << "ID(1) : " << g.ID(1) << endl;
cout << "OD(1) : " << g.OD(1) << endl;
cout << "TD(1) : " << g.TD(1) << endl;
g.removeVertex();
cout << "eCount : " << g.eCount() << endl;
return 0;
}
小结
邻接链表法使用链表对图相关的数据进行存储
每一个顶点关联一个链表,用于存储边相关的数据
所有顶点按照编号被组织在同一个链表中
邻接链表法实现的图能够支持动态添加/删除顶点
3、时间复杂度的对比分析
小结论
-MatrixGraph适用于内存资源富足的场合(性能较好)
-ListGraph适用于内存资源受限的场合(节省空间)