图的embedding问题
图的embedding问题
[摘要]:随着word2vec模型的提出,embedding问题开始逐渐引起大家的注意。在如今大数据背景的驱动下,商品、行为、用户等实体之间的关系越来越复杂化、网络化,而word2vec是sequence embedding的,故其表示能力较弱,已不适合表示当下的复杂数据,因此人们又提出了graph embedding,即通过某种方法,将大型的图进行embedding,从而得到数据相关性很强的低维稠密序列,方便我们进行分析处理。本文章针对graph embedding问题,使用deep walk方法解决一个简单的图嵌入问题。
关键词:图;embeding;word2vec
一、问题的提出
对向量进行embedding能够使距离相近的向量对应的物体有相近的含义,在自然语言处理中,我们用词距表示语义间的接近程度,进而通过用词向量的方式表征词的语义信息,即通过一个嵌入空间使得语义上相似的单词在该空间内距离很近,这便是word2vec的实质。这样的处理方法,给人们了很大的启示——我们可以对任意稀疏表示的向量、数据(例如图)进行embedding,从而得到稠密、低维的向量表示。
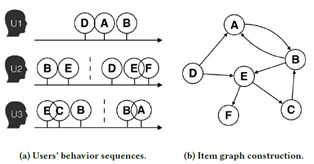
在如今互联网流行的世界中,我们最常见的数据结构可能会是图,例如在电子商务的应用场景下,用户行为与物品关系可以组成一个有向图,如图1所示,在加入物品属性后甚至会组成知识图谱。
在面对这样复杂的图结构时,传统的sequence embedding方法显得力不从心。因此,我们可以利用图节点之间共同出现的关系(共现关系)来学习节点的向量表示。Deep walk算法通过随机游走(Radom walk)来进行图中的节点采样。Radom walk基于图的深度优先遍历,唯一不同的是该遍历方法允许访问已经访问过的节点。
现在我们提出一个简单的embeding问题:某社交网站拥有300名用户(顶点),和450条用户联系(无向边),我们使用deep walk算法对该图进行embeding从而得到编码后的向量表示。
首先,通过networkx工具,将数据集中的连接关系进行可视化,结果如图2所示。图中的每个顶点代表一个用户,顶点间的连线表示用户之间拥有社会关系,同时,孤立的顶点表示该用户与其他用户没有关系。
通过对该图做embeding,我们可以得到信息量较大(稠密)、维度较低的向量表示,得到向量表示以后,我们可以根据标签等数据,去解决更为复杂的问题,例如推荐系统、影响力最大化等。所以该问题具有较深刻的意义。接下来本报告将围绕着该问题,通过deep walk算法来构建相关模型,求得最终结果,并且做出相应评估。
二、deep walk算法执行步骤
Deep Walk算法主要分为两个步骤,首先进行随机游走(Random Walk)采样节点序列,其次是使用word2vec学习表达向量。具体的算法实现如图3所示。
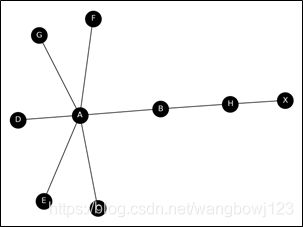
随机游走是基于图的深度优先遍历的,同时允许遍历曾经遍历过的节点。为了容易说明随机游走的执行过程与结果,仅截取数据集的前9个顶点组成一个简单的无向图,如图4所示。
首先是随机游走的实现:先确定一个最大步长S、和迭代次数N,并随机选取一个顶点Vi作为起始点,之后随机选取Vi的邻接顶点作为下一次遍历起始顶点,整体遍历方法属于图的深度优先遍历,直到达到最大步长或者遍历到度为1的顶点,之后重复上述步骤,直到遍历完为止。
根据上述步骤,我们对图4作随机游走,设定迭代次数为1,步长为2,那么我们将得到结果:[[‘E’, ‘A’], [‘H’, ‘B’], [‘F’, ‘A’], [‘X’, ‘H’], [‘C’, ‘A’], [‘D’, ‘A’], [‘B’, ‘A’], [‘A’, ‘D’], [‘G’, ‘A’]],将结果绘制为有向图,可得到图4。由于每次随机选取起始节点,故每次运行的结果都不一样,并且如果迭代次数设置的较大,那么会重复地遍历顶点。
在得到了节点的采样序列之后,我们将该序列输入进word2vec模型,通过skip gram方法进行学习。该学习方法其实是对采样序列进一步采样,但是采样方法不同于上一步中随机深度优先的搜索,而是有概率控制的有偏的遍历方式:通过引入两个超参数p、q来将宽度优先与深度优先同时引入采样方式中,这样做的好处是在充分探索了图的全局结构性(深度优先搜索)的同时也兼顾到了图的局部相似性(宽度优先搜索)。因此,可以说node2vec是对deep walk的进一步拓展与延申。
核心源码如下:
# 读数据集
G = nx.read_edgelist('../data/wiki/edges.txt',
create_using=nx.DiGraph())
# deepwalk的实现,每次游走9个顶点。外层迭代70次
model = DeepWalk(G, walk_length=9, num_walks=70)
# word2vec模型进行训练
model.train(window_size=5, iter=3)
embeddings = model.get_embeddings()
print('embeding后的向量个数:' + str(len(embeddings.values())))
# 写入文件
with open('embeding.txt') as file:
file.write(embeddings)
最终将得到300个节点的embedding向量。如图6所示。

三、进一步的应用
在得到了图的embeding向量之后,为了令这些向量发挥作用,我们为每个顶点指定一个标签或者说是种类(0-7)表示该顶点社会关系的复杂度,之后通过多分类的训练方法,将embedding后的顶点向量作为输入进行模型训练,并最终进行一定的可视化。可视化结果如图7所示。(为了便于可视化,通过fit_transform方法对向量进行了降维操作)
四、总结
图的embedding是图论在机器学习与深度学习中的重要应用。在面对图的数据集时,传统的one-hot编码会令训练数据集过于稀疏或维度过高,不利于我们的模型提取特征。通过embedding得到较为稠密的数据向量表示会大大加快训练速度与准确度,有利于处理大数据等及其复杂的数据集。
五、参考文献
[1] 龚劬. 图论与网络最优化算法[M]. 重庆: 重庆大学版社.
[2] Bryan Perozzi, Rami Al-Rfou, Steven Skiena. DeepWalk: Online Learning of Social Representations[J].