数据结构学习笔记-栈和队列
主要内容:
3.1 栈和队列的定义和特点
3.2 栈的表示和操作的实现
3.3 栈的应用
3.4 队列的表示和操作的实现
3.1 栈和队列的定义和特点
从数据结构的角度看: 栈和队列是操作受限的线性表—数据元素之间是线性关系, 插入和删除操作限定在一端进行
串是元素受限的线性表—数据元素类型为字符型
从数据类型的角度看: 栈和队列是与线性表大不相同的抽象数据类型
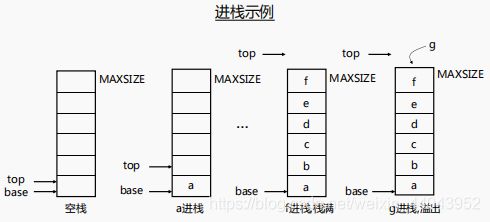
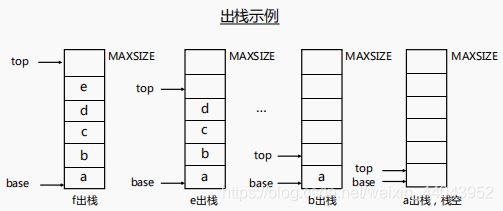
一、栈的定义和特点
1、限定在表尾进行插入和删除操作的线性表
表尾称为栈顶(top):允许插入和删除的一端
表头称为栈底(base) :固定不变的一端
2、特点:后进先出(LIFO) 例如:一摞盘子;火车的调度
3、栈的基本操作
初始建栈;判断栈空、栈满;进栈、出栈;取栈顶元素

二、队列的定义和特点
1、队列是限定在表的一端进行删除,在表的另一端进行插入的线 性表
队头(front):允许删除的一端叫队头;
队尾(rear):允许插入的一端叫做队尾
3.2 栈的表示和操作的实现
一、顺序栈的表示和实现
1、基本思想
1)用一组地址连续的存储单元依次存放从栈底到栈顶的数据元素
2)同时附设指针 top 指向栈顶,base指向栈底
3)采用动态分配原则,栈满时可按预定的增量追加存储空间
2、顺序栈的表示
#define MAXSIZE 100
Typedef struct
{
SElemType *base;
SElemType *top;
int stacksize; //追加空间时用到
} SqStack;
SqStack s;
//使用时:s.base,s.top, s.stacksize
1)base称为栈底指针,始终指向栈底; 当base=NULL时,表明栈结构不存在
2)top为栈顶指针 top的初值指向栈底,即top=base表示栈空 当栈非空时,top的位置指向栈顶元素的下一个位置
3)stacksize :当前栈可使用的内存容量
(以sizeof (SElemType) 为单位)
顺序栈的初始化
[算法步骤]
1)动态分配最大容量为MAXSIZE的数组空间
2)栈底指针base指向这段空间
3)栈顶指针top初值设为base,表示栈空
[算法描述]
Status InitStack (SqStack &S)
{
S.base=new SElemType[MAXSIZE];
if (!S.base)
exit(OVERFLOW);
S.top=S.base;
S.stacksize=MAXSIZE;
return OK;
}
入栈操作
[算法步骤]
1)判断是否栈满,满则返回ERROR
2)新元素压入栈顶,栈顶指针加1
[算法描述]
Status Push(SqStack &S, SElemType e)
{
if (S.top-S.base>=S.stacksize)
return ERROR;
*S.top++=e; // *S.top=e; S.top=S.top+1;
return OK;
}
取栈顶元素
[算法步骤]
1)判断是否栈空,空则返回ERROR
2)返回栈顶元素,栈顶指针保持不变
[算法描述]
SElemType GetTop(SqStack S)
{
if (S.top==S.base)
return ERROR;
return *(S.top-1); //与e=*--S.top不同
}
二、链栈的表示和实现
1、基本思想
1)用链表表示栈,动态申请和释放结点,不存在栈满的问题
2)栈顶:链表的第一个结点 栈底:不设栈底指针
3)一般不设头结点
2、链栈的表示
Typedef struct SNode
{
SElemType data;
struct SNode *next;
} StackNode,*LinkStack;
LinkStack s; //使用:s->data,s->next
链栈的初始化
[算法步骤]
构造不带头结点的空栈,直接将栈顶指针置空即可
[算法描述]
Status InitStack(LinkStack &S)
{
S=NULL;
return OK;
}
入栈操作
[算法步骤]
1)为入栈元素e分配空间,用指针p指向该空间
2)将新结点数据域置为e
3)将新结点插入栈顶
4)修改栈顶指针为p
[算法描述]
Status Push(LinkStack &S, SElemType e)
{
p=new StackNode;
if (!p)
exit(OverFlow);
p->data=e;
p->next=S;
S=p;
return OK;
}
出栈操作
[算法步骤]
1)判断栈是否为空,若空则返回ERROR
2)将栈顶元素赋值给e
3)临时保存栈顶元素的空间以备释放
4)修改栈顶指针为指向新的栈顶元素
5)释放原栈顶元素的空间
[算法描述]
Status Pop (LinkStack &S, SElemType &e)
{
if (!S)
return ERROR;
e=S->data;
p=S;
S=S->next;
delete p;
return OK;
}
取栈顶元素
[算法步骤]
1)判断是否栈空,空则返回ERROR
2)返回栈顶元素,栈顶指针S保持不变
[算法描述]
SElemType GetTop (LinkStack S)
{
if (S)
return S->data;
}
3.3 栈的应用
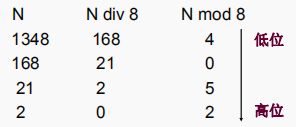
一、数制转换
十进制数N和d进制数的转换基于下列原理:
N=(N div d)*d+N mod d
(div为整除运算,mod为求余运算)
例如: (1348)10=(2504)8
二、括号匹配
用“期待的急迫程度”来描述匹配原则,期待程度最大的括号始 终处于栈顶
1)设置一个栈,每读出一个左括号则作为最急迫的期待入栈 ,栈中其他未消解的左括号期待的急迫程度均降一级
2)读到右括号,或者使处于栈顶的最急迫期待消解,或者是不匹配的情况
3)在算法开始和结束时,栈均为空
三、表达式求值
1、运算符间的优先级关系
1)先乘除,后加减
2)相同优先级,从左算到右
3)先内括号,后外括号
2、左括号
比括号内的算符的优先级低
比括号外的算符的优先级高
3、界限符#:优先级最低
4、使用两个工作栈:
OPND栈:存操作数或运算结果
OPTR栈:存运算符和界限符
例题:x= #10-5*3+7#
应该等于2,解释成22是错误的
1、初态: 置OPND栈为空;将“#”作为OPTR栈的栈底元素;
2、依次读入表达式中每个字符到ch:
1)若是操作数则ch进入OPND栈;
2)若是运算符则ch与OPTR栈的栈顶运算符进行优先级比较:
①若ch优先级高,则入栈OPTR
②若ch优先级低,则出栈OPTR栈顶元素,并连续出栈OPND两个元素 ,将计算结果压入OPND栈
③若读入“)”,OPTR的栈顶元素若为“(”,则出栈“(”
④若读入“#”,OPTR的栈顶元素也为“#”,则OPTR出栈“#”,算法结束
四、子程序调用
1、进入被调用子程序前,做三件事:
1)将实际参数、返回地址传递给被调子程序
2)保存被调子程序的局部变量
3)将控制权转移到被调子程序入口
2、从被调子程序返回调用程序时,做三件事:
1)保存被调子程序的计算结果
2)释放被调子程序的数据区
3)将控制权转移到调用程序的断点处
3、利用调用栈保存实际参数、局部变量、返回地址以及计算结 果,形成一条 :
1)调用前,在栈顶分配数据区
2)调用后,释放数据区
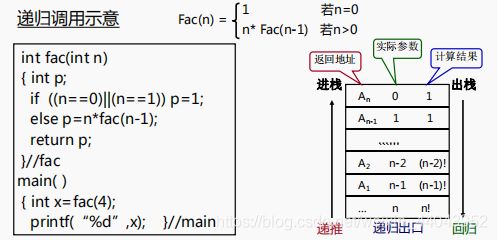
五、栈与递归
1、递归调用类似于子程序调用,只不过调用的是同一个子程序
2、递归算法用于解决三类问题:
- 数据是递归定义的(阶乘的定义)
- 数据结构是递归的(树的定义)
- 问题是递归实现的(二叉树的算法)
3、递归有递归出口、递推和回归三要素
出口条件不满足时:递推;否则:回归
void p(参数表)
{
if(递归结束条件成立)
直接求解退出递推;
else p(较小的参数);
}
4、需设一个递归工作栈控制递归调用,每一个递归层次构成一 个工作记录(实际参数、局部变量、返回地址及计算结果)
5、递推:每进入一层递归,产生一个新的工作记录压栈 回归:每退出一层递归,从栈顶弹出一个工作记录
6、栈顶的工作记录代表正在执行的层次,称为“活动记录”, 指向活动记录的栈顶指针称为“当前环境指针”
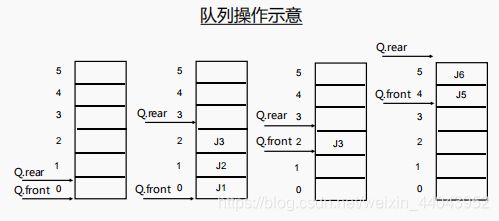
一、循环队列—队列的顺序表示和实现
1、基本思想
1)用一组地址连续的存储单元依次存放从队头到队尾的元素
2)附设两个指针
front :指示队首元素的位置
rear:指示队尾元素的下一个位置
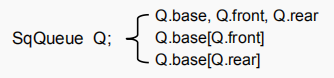
2、队列的顺序存储结构
#define MAXQSIZE 100
typedef struct
{
QElemType *base;
int front; //用下标表示队首、队尾
int rear;
}SqQueue;
1)初始状态:Q.front=Q.rear=0;
2)队空: Q.front==Q.rear;
3)队满: Q.rear>=MAXQSIZE; (假溢出)
4)队长: Q.rear-Q.front;
5)进队时:先入队元素,后修改指针
Q.base[Q.rear]=e; Q.rear=Q.rear+1;
6)出队时:先出队元素,后修改指针
e=Q.base[Q.front]; Q.front=Q.front+1;
7)队满时进队发生溢出错误,队空时出队作队空处理
3、循环队列的构造
1)与顺序队列的表示相同,看作首尾相连的环状结构
2)通过取模运算实现队首、队尾指针加1时从下标MaxSize –1 回到 0
队首指针加1: Q.front=(Q.front+1)% MAXSIZE
队尾指针加1: Q.rear=(Q.rear+1)% MAXSIZE

4)初态:Q.front=Q.rear=0;
5)队空条件:Q.front=Q.rear
6)队满条件:(Q.rear+1)%MAXSIZE=Q.front
7)队列长度:(Q.rear-Q.front+MAXSIZE)%MAXSIZE
队满条件构造
Q.front==Q.rear:区分队空or队满?
1)设置标志位flag区分:flag为0队空,flag为1队满
2)结合计数器counter终值区分:入队加1,出队减1
3)少用一个存储单元:约定Q.front指向Q.rear的下一个位置时表示队满,Q.rear所指位置不存放元素
4、循环队列的基本操作
循环队列的初始化
[算法步骤]
1)动态分配最大容量为MAXQSIZE的数组空间
2)基地址指针base指向这段空间
3)队首指针front和队尾指针rear置为0,表示队列为空
[算法描述]
Status InitQueue (SqQueue &Q)
{
Q.base=new QElemType[MAXQSIZE];
if (!Q.base)
exit(OVERFLOW);
Q.front=Q.rear=0;
return OK;
}// InitQueue
求队列长度
[算法步骤]
返回(Q.rear-Q.front+MAXQSIZE)%MAXQSIZE的值
[算法描述]
int QueueLength(SqQueue Q)
{
return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE);
}
入队操作
[算法步骤]
1)判断队列是否为满,为满则返回ERROR
2)将新元素插入队尾
3)队尾指针循环加1
[算法描述]
Status EnQueue (SqQueue &Q, QElemType e)
{
if ((Q.rear+1)%MAXQSIZE==Q.front)
return ERROR;
Q.base[Q.rear]=e;
Q.rear=(Q.rear+1)%MAXQSIZE;
return OK;
} //EnQueue
出队操作
[算法步骤]
1)判断队列是否为空,为空则返回ERROR
2)保存队首元素
3)队首指针循环加1
[算法描述]
Status DeQueue(SqQueue &Q, QElemType &e)
{
if (Q.rear==Q.front)
return ERROR;
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXQSIZE;
return OK;
} //DeQueue
取队首元素
[算法步骤]
1)判断队列是否为空,为空则返回ERROR
2)返回队首元素
3)队首指针保持不变
[算法描述]
Status GetHead(SqQueue Q)
{
if (Q.front!=Q.rear)
return Q.base[Q.front];
} //GetHead
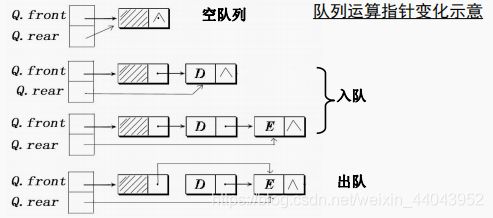
二、链队列—队列的链式表示和实现
1、基本思想
1)实质是带头结点的线性链表
2)附设两个指针:
队头指针Q.front指向头结点
队尾指针Q.rear 指向尾结点
(3)初始状态 Q.front=Q.rear
2、链队列的表示
typedef struct QNode //队列结点
{
QElemType data;
struct QNode *next;
} QNode, *QueuePtr;
typedef struct {
QueuePtr front; // 队首指针
QueuePtr rear; // 队尾指针
} LinkQueue; //链队列类型
LinkQueue Q;
//Q.front—队首指针
//Q.rear —队尾指针
//Q.front->next
//Q.rear->data
3、链队列的实现
链队列的初始化
[算法步骤]
1)生成新结点作为头结点,队首和队尾指针指向该结点
2)头结点的指针域置空
[算法描述]
Status InitQueue (LinkQueue &Q)
{
Q.front=Q.rear=new QNode;
if (!Q.front)
exit (OVERFLOW);
Q.front->next=NULL;
return OK;
} //InitQueue
[算法步骤]
1)为入队元素分配结点空间,用指针p指向该结点
2)将新结点数据域置为e
3)将新结点插入到队尾
4)修改队尾指针为p
[算法描述]
Status EnQueue (LinkQueue &Q, QElemType e)
{
p=new QNode;
if (!p)
exit(OVERFLOW);
p->data=e;
p->next=NULL;
Q.rear->next=p; //尾插法入队
Q.rear=p;
return OK;
} //EnQueue
链队列的出队
[算法步骤]
1)判断队列是否为空,为空则返回ERROR
2)记录队首元素的空间以备释放
3)修改队首指针,指向下一个结点
4)判断出队元素是否为下一个结点,若是则将队尾指针重新 赋值,指向队首结点
5)释放原队首元素的空间
[算法描述]
Status DeQueue (LinkQueue &Q, ElemType &e)
{
if (Q.front==Q.rear)
return ERROR;
p=Q.front->next;
e=p->data;
Q.front->next=p->next;
if (Q.rear==p)
Q.rear=Q.front;
delete p;
return OK;
} //DeQueue
取队首元素
[算法步骤]
1)判断队列是否为空,不为空则返回返回队首元素
2)队首指针保持不变
[算法描述]
Status GetHead (LinkQueue Q)
{
if (Q.front!=Q.rear)
return Q.front->next->data;
} //GetHead
队列的应用举例:舞伴问题
1)所有男士或女士放在同一个数组,根据性别决定进入男队 还是女队
2)两个队列构造完毕,依次将两队当前的队首元素出队配成 舞伴,直至某队列变为空队列为止
3)若某队列仍有等待配对者,则输出排在队首的等待者姓名 ,将成为下一轮舞曲开始时第一个获得舞伴的人