卷积神经网络(2)——CNN前向传播过程详细剖析(Python实现)

在上一篇博文中，我们详细学习了CNN的基本原理，那么在这篇博客里，我们就用python来实现一遍卷积神经网络前向传播，而对于反向传播，因为在一些深度学习的框架中，我们只需要花心思做好前向传播的部分，框架会自动为我们完成反向传播，同时，CNN反向传播有点难，待日后我完全了解了就会补发上来的

卷积神经网络的前向传播

前期准备工作

(1) 关于python里面的维度说明

在之前我们的学习中，常常将一张RGB图像的维度写成：H x W x C
其中，H代表图像的高，W代表图像的宽，C代表图像的通道数，$当然如果有多个样本，我们就写成mxHxWxC$，那么，在python中我们是怎样理解高维度矩阵的表示的呢？这对我们后面的步骤非常重要

#假设我们的输入图像有一个样本，每个样本高度H为2，宽度W为3，有3个通道,那么我们应该这样输入
a_prev = [[[[1,2,3],[4,5,6],[7,8,9]],[[3,2,1],[6,5,4],[9,8,7]]]]
A_prev = np.array(a_prev)
print(A_prev.shape)
print(A_prev)
"""
第一个维度：输入矩阵的样本数
第二个维度：输入矩阵的高
第三个维度：输入矩阵的宽
第四个维度：输入矩阵的通道数
"""

输出结果如下：

(1, 2, 3, 3)
[[[[1 2 3]
   [4 5 6]
   [7 8 9]]

  [[3 2 1]
   [6 5 4]
   [9 8 7]]]]

这里给大家分享一个博主个人理解的小窍门：对于这些高维矩阵，我们把每一个部分（上面以换行隔开了每一个部分）看成一层，然后由上到下堆叠，下面我画一个图片来解释怎么看：

我们可以看出该矩阵有3个通道，每个通道都是2x3的矩阵
因此，我们能看到矩阵的第一个维度是样本数量，第二个维度是通道数，第三个维度是图像的高H，第四个维度是图像的宽W，对于后面我们要用到的W矩阵也是类似的

(2)填充操作：np.pad()的详细使用说明

在这一步的设计中，我们打算给输入图像进行周围填充0像素的操作
在此之前，我们先来回顾一下填充有什么好处：

• 合适的填充可以让我们的输入图像在经过卷积操作时不会变小，尤其说对于比较深层的卷积神经网络，这个是非常重要的
• 填充操作可以让我们更好地保留图像边缘部分的信息
  在python里面，我们对矩阵进行填充可以使用np.pad方法，我们先来看看它的函数原型：

pad(array,pad_width,mode,**kwars)

1. 第一个参数：需要填充的矩阵
2. 第二个参数：表示每个轴（或者说维度）在边缘需要填充的数值数目，pad_width的参数格式是这样的：(($widt{h}_1^{[1]},widt{h}_2^{[1]}$),($widt{h}_1^{[2]},widt{h}_2^{[2]}$),$\cdots$,($widt{h}_1^{[2]},widt{h}_2^{[2]}$))
   这里width的上标[1]表示是第一个维度，下标表示该维度两边需要填充的数字的宽度
   比如说我们的矩阵的维度为[3,2]，即有两个维度，那么对于这个矩阵而言，如果我想要它的两个维度的两边填充宽度为1的数字，那么pad_width可以写成：((1,1),(1,1))
   $另外说明：如果某一维度写成了(0,0)，那么表示该维度的两边都不需要填充$
3. mode——表示填充的方式（取值：str字符串或用户提供的函数),下面列举出常用的填充方式：
   (1) ‘constant’——表示连续填充相同的值，每个轴可以分别指定填充值，constant_values=（x, y)时前面用x填充，后面用y填充，缺省值填充0
   (2) ‘edge’——表示用边缘值填充
   (3) maximum’——表示最大值填充
   (4) ‘minimum’——表示最小值填充
   (5) ‘mean’——表示均值填充
   (6) ‘median’——表示中位数填充
   …
4. 第四个参数：要填充的值

下面我们通过实例来看看：

import numpy as np

A_prev = np.ones((1,2,3,3))   #假设我们神经网络的输入矩阵：单样本，三通道，每个通道为2x3
A_padding = np.pad(A_prev, ((0,0),(1,1),(1,1),(0,0)), 'constant')  #缺省第四个参数，代表填充0
print(A_padding)

在这样的操作之后，A_prev到A_padding的变化如下所示（下图中每一个矩阵代表A_prev的每一个通道）：$$\begin{gathered} \left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\end{array}\right]\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\end{array}\right]\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\end{array}\right] \\ \Downarrow \end{gathered}$$
$$\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 1& 1& 1& 0\\ 0& 1& 1& 1& 0\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 1& 1& 1& 0\\ 0& 1& 1& 1& 0\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 1& 1& 1& 0\\ 0& 1& 1& 1& 0\\ 0& 0& 0& 0& 0\end{array}\right]$$
输出的A_padding是这样的：

[[[[0. 0. 0.]
   [0. 0. 0.]
   [0. 0. 0.]
   [0. 0. 0.]
   [0. 0. 0.]]

  [[0. 0. 0.]
   [1. 1. 1.]
   [1. 1. 1.]
   [1. 1. 1.]
   [0. 0. 0.]]

  [[0. 0. 0.]
   [1. 1. 1.]
   [1. 1. 1.]
   [1. 1. 1.]
   [0. 0. 0.]]

  [[0. 0. 0.]
   [0. 0. 0.]
   [0. 0. 0.]
   [0. 0. 0.]
   [0. 0. 0.]]]]

大家如果按照上面博主画的那幅图来推理的话得到的矩阵也是一样的

(3)对A_padding取切片

因为我们做卷积的时候，是对A_padding的局部计算的，也就是滤波器会在整个A_pqdding矩阵上滑动，对滤波器所覆盖的地方做卷积计算，因此，我们先要弄明白怎么对高维度矩阵做切片处理：
一般来讲，格式是这样的:A[$demensio{n}_1$_start : $demensio{n}_2$ : end, … $demensio{n}_n$_start : $demensio{n}_n$_end]
假设我们的滤波器组中每个通道的滤波器的维度为3x3，那么我们就需要在A_padding的每个通道上，分割出和滤波器大小相同的3x3的矩阵，具体操作如下：

A_padding = np.pad(A_prev, ((0,0),(1,1),(1,1),(0,0)),'constant')  #这个是上面的例子
A_slide = A_padding[0] #先取A_prev的第一个样本
print(A_slide[0:3, 0:3, :])

输出：

[[[0. 0. 0.]
  [0. 0. 0.]
  [0. 0. 0.]]

 [[0. 0. 0.]
  [1. 1. 1.]
  [1. 1. 1.]]

 [[0. 0. 0.]
  [1. 1. 1.]
  [1. 1. 1.]]]

对于a_stride的第一个和第二个维度，也就是矩阵的高和宽，我们是想分割成3x3大小的，因此使用0:3，对于通道我们不用分割，因此，在这个维度的位置上使用“ ： ”就表示不进行分割
这样一来，我们就得到了一个3x3x3的立方体了
如果你没还没有搞清楚为什么是0:3，那么请看看下面这副对于2x2矩阵的分割就明了了：

(4)单次的卷积操作

我们先来看看一个卷积层在干嘛：

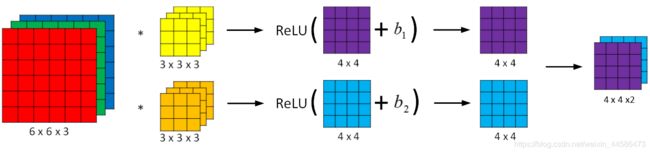
没错，一个卷积层可以有很多个滤波器组，然后我们的输入图像分别和每一个滤波器组做卷积，分别得到各自的输出，到此为止，后面什么加b，应用Relu函数什么的，我们暂且不看，因为我们现在只是关心卷积这个操作，而单次卷积，就是输入图像和一个滤波器组卷积的过程
好的，现在我们的眼中只有下面这幅图：

因为卷积操作就相当于DNN里面的$W^{[l]}{A}_{prev}$
因此，我们就可以写出单次卷积的函数了：

def single_conv(A_slide, W): #请注意：这里的A_slide是A_prev的局部，也就是和滤波器重叠的部分
    """
    这个函数是对于一个滤波器组而言的
    """
    s = np.multiply(A_slide, W)  #卷积的步骤1：A_slide和滤波器对应元素相乘
    Z = np.sum(s)  #卷积步骤2：将s矩阵的所有元素相加
    return Z   #说明：这里返回的是一个数，到时候是要赋值给新矩阵的

这里还需要说明一点：所谓的单次卷积，其实是两个“小立方体”的卷积（我们刚刚不是把输入的矩阵分割成了一个3x3x3的小立方体嘛，然后每一个滤波器组也是一个fxfx3的立方体，我们的单次卷积就是这两个小立方体的卷积计算）
我们来测试一下：

b = [[[1,2,3],[4,5,6]],[[7,8,9],[1,2,3]]]
B = np.array(b)
c = [[[3,2,1],[1,2,3]],[[1,2,3],[3,2,1]]]
C = np.array(c)
S = single_conv(b,c)
print(S)

输出结果为102

CNN卷积层的前向传播

对于前向传播函数，我们需要的参数有:A_prev（输入矩阵), W, b, 超参数字典hyper_parameters（这个字典里面包含了：步长stride，填充数padding）
首先，我们得需要读出输入矩阵的维度：

(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
(n_C, f, f, n_C_prev) = W.shape  #n_C是这一个卷积层中滤波器组的数量,n_C_prev是A_prev的通道数

下面，我们就该对A_prev进行填充操作了：

A_padding = np.pad(A_prev, ((0,0),(1,1),(1,1),(0,0)),'constant')

好的，我们继续：下一步就该从字典里面读取需要的超参数padding和stride了，一会儿我们计算输出矩阵的维度时需要用得上

padding = hyper_parameters["padding"]
stride = hyper_parameters["stride"]

我们离胜利不远了！下面，我们该计算一下输出的Z矩阵的维度，以及初始化一个全零的Z矩阵
还记得我们的计算H和W的公式吗?$$\begin{gathered} n\_H=\lfloor \frac{n\_H\_prev+2p-f}{s}+1\rfloor \\ n\_W=\lfloor \frac{n\_W\_prev+2p-f}{s}+1\rfloor \end{gathered}$$

n_H = int((n_H_prev + 2 * padding - f) / stride + 1)
n_W = int((n_W_prev + 2 * padding - f) / stride + 1)
Z = np.zeros((m, n_H, n_W, n_C)  #n_C是Z的通道数

下面正式开始计算前向传播，但是在此之前，我们还得确保一件事情，就是如果我们的三通道矩阵只是和一个滤波器组（当然，这个滤波器组的通道数必须和输入图像一致）卷积，那么输出的结果依然是单通道的矩阵，然后至于计算，我这里再举一个实际的例子，便于大家理解：
首先，假设我们的输入矩阵经过padding之后的三个通道长这样：$$\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 2& 0\\ 0& 3& 4& 0\\ 0& 5& 6& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 2& 0\\ 0& 3& 4& 0\\ 0& 5& 6& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 2& 0\\ 0& 3& 4& 0\\ 0& 5& 6& 0\\ 0& 0& 0& 0\end{array}\right]$$
然后，我们使用的一个滤波器组矩阵的三个通道张这样：（为了简单起见，我把它们都设为1）$$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$$
假设步长stride=1,padding这里我们可以看出来是1,通过计算可知输出矩阵Z的维度为3x2x1
Z矩阵左上角第一个元素是三个通道和对应滤波器卷积之后的加和：
Z[0][0] = (0x1 + 0x1 + 0x1 + 0x1 + 1x1 + 2x1 + 0x1 + 3x1 + 4x1) +
(0x1 + 0x1 + 0x1 + 0x1 + 1x1 + 2x1 + 0x1 + 3x1 + 4x1) +
(0x1 + 0x1 + 0x1 + 0x1 + 1x1 + 2x1 + 0x1 + 3x1 + 4x1)
每一个括号对应每个通道的卷积计算，Z的其他位置元素计算方法类似
这里我们得用几个for循环：

  for i in range(m):
    a_stride = A_padding[i]
    for h in range(n_H):
      for w in range(n_W):
        for c in range(n_C):
          Z[i,h, w, c] = single_conv(a_stride[h * stride:h * stride +f, w * stride:w * stride+f,:], W[c,:,:,:])
          """
          W的第二个维度的参数是和a_stride一样的通道数，我们把它设置为:就是不取切片，那么也就和a_stride的通道数匹配了
          W的第一个维度的参数是滤波器组的个数，我们设置为一个数字c表示每一次和a_stride卷积的只有一个滤波器组
          如果这第一个参数不设置为c或者说不取切片的话，那么就是说所有的滤波器组在这一次的卷积中都会和a_stride卷积
          """
    Z = Z + b
    return Z

那么，完整的前向传播的代码如下：

javascript
def conv(A_prev, W, b, hyper_parameters):
  (m, n_H_prev, n_W_prev,n_C_prev) = A_prev.shape
  A_padding = np.pad(A_prev, ((0,0),(1,1),(1,1),(0,0)),'constant')
  (n_C, f, f, n_C_prev) = W.shape
  padding = hyper_parameters["padding"]
  stride = hyper_parameters["stride"]
  n_H = int((n_H_prev + 2 * padding - f) / stride + 1)
  n_W = int((n_W_prev + 2 * padding - f) / stride + 1)
  Z = np.zeros((m, n_H, n_W, n_C))  #n_C是Z的通道数
  for i in range(m):
    a_stride = A_padding[i]
    for h in range(n_H):
      for w in range(n_W):
        for c in range(n_C):
          Z[i,h, w, c] = single_conv(a_stride[h * stride:h * stride +f, w * stride:w * stride+f,:], W[c,:,:,:])
  Z = Z + b
  A, activation_cache = Relu(Z)
  linear_cache = (A_prev, W, b)
  cache = (activation_cache, linear_cache)
 
  return (A, cache)

下面我们来测试一下：

A_prev = np.ones((1,2,3,3))
hyper_parameters = {"padding":1, "stride":1}
W = np.ones((2,3,3,3))
b = 1   #numpy里面的广播机制
Z,cache = conv(A_prev, W, b, hyper_parameters)
print(Z)

我们看看结果和我们用笔算的是否一致？

[[[[13. 13.]
   [19. 19.]
   [13. 13.]]

  [[13. 13.]
   [19. 19.]
   [13. 13.]]]]

正确，说明我们的前向传播算法没什么问题
至于我们在函数中加入的Relu函数，在本例中可有可无，因为矩阵中的值都大于0，所以效果是一样的

CNN池化层的前向传播

个人觉得池化层的前向传播和卷积层的前向传播，在前面的处理方式几乎相同，只是后面的操作取决于我们想max pooling还是average pooling了
我们再一次回顾一下这两种池化的方法是怎么用的：

至于求掩码所覆盖区域的最大值或者是均值，在numpy中，我们可以使用np.max和np.mean来实现
下面，我们再来逐句剖析池化层的前向传播：
首先，我们需要传入的参数有：CONV层计算得到的A（但是对应POOL层来讲这个A已经是前一层的了，因此在函数的形参中，我们还是使用A_prev），hyper_parameters2:池化层的超参数字典，这里存放了掩码的尺寸f，以及掩码滑动的步长stride，最后，我们还需要一个模式mode字符串，来告诉程序我们是想使用最大池化还是均值池化

def pool(A_prev, hyper_parameters, mode = "max"):

下面，我们依然是要得到A_prev的维度，以及从超参数字典中获取我们需要的参数
（f和stride是用于后面计算池化输出矩阵的维度的）

(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
f = hyper_parameters["f"]
stride = hyper_parameters["stride"]

在获取了这些信息之后，我们就要开始计算输出矩阵的维度，以及初始化这个矩阵了：

n_C = n_C_prev
n_H = int((n_C_prev - f) / stride + 1)
n_W = int((n_W_prev - f) / stride + 1)
A_pool = np.zeros((m, n_H, n_W, n_C))

下面我们需要几个for循环来更新A_pool里面的值：

for i in range(m):
  for h in range(n_H):
     for w in range(n_W):
        for c in range(n_C):
          if mode == "max":
            A_pool[i, h, w, c] = np.max(A_prev[:,:,h * stride:h * stride+f, w * stride: w * stride + f])
          elif mode == "average":
            A_pool[i, h, w, c] = np.mean(A_prev[:,:,h * stride:h * stride+f, w * stride: w * stride + f])
#同样的，把A_prev和hyper_parameters作为缓存，反向传播的时候用得上
cache = (A_prev, hyper_parameters)
return (A_pool, cache)

池化层前向传播的完整代码如下：

的矩阵，还是刚刚上面我们在测试例子中计算出来的矩阵，掩码我们选用的f = 2, stride = 1
```javascript
def pool(A_prev, hyper_parameters, mode = "max"):
  (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
  f = hyper_parameters["f"]
  stride = hyper_parameters["stride"]
  n_C = n_C_prev
  n_H = int((n_H_prev - f) / stride + 1)
  n_W = int((n_W_prev - f) / stride + 1)
  A_pool = np.zeros((m,n_H, n_W, n_C))
  for i in range(m):
    for h in range(n_H):
       for w in range(n_W):
          for c in range(n_C):
            if mode == "max":
              A_pool[i, h, w, c] = np.max(A_prev[:,:,h * stride:h * stride+f, w * stride: w * stride + f])
            elif mode == "average":
              A_pool[i, h, w, c] = np.mean(A_prev[:,:,h * stride:h * stride+f, w * stride: w * stride + f])

  cache = (A_prev, hyper_parameters)  
  return (A_pool, cache)

我们同样来测试一下：

hyper_parameters2 = {"f":2, "stride": 1}
A_pool, cache = pool(A, hyper_parameters2, mode = "max")
print(A_pool)

结果如下：

[[[[19. 19.]
   [19. 19.]]]]  #计算正确

至此，我们就完成了CNN卷积层和池化层对于每一层而言的前向传播计算
还有一个全连接层，那个的前向传播和我们之前学习的DNN类似

参考资料：
[1]:https://blog.csdn.net/qq_34650787/article/details/80500407
[2]:https://blog.csdn.net/u013733326/article/details/80086090
[3]:https://blog.csdn.net/holmes_mx/article/details/82813865