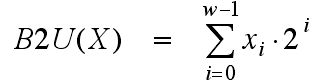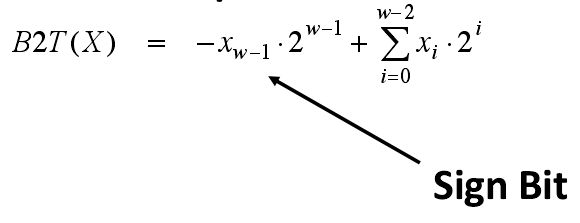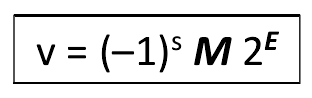《深入理解计算机系统》Part1 02：信息的表示和处理

摘要：本章首先介绍了信息在计算机中的表示方法，其次主要介绍了整数和浮点数在计算机中的二进制表示方法及其运算。
关键词：大端和小端；无符号数编码；有符号数编码；浮点数
目录：
  1 信息的表示
  2 无符号整数
    2.1无符号整数编码
    2.2无符号整数的运算
  3 有符号数
    3.1有符号数编码
    3.2有符号数运算
  4 浮点数
    4.1 浮点数表示方法
    4.2 浮点数运算

1 信息的表示

数据在计算机中都是用二级制表示，可以简单的将其理解为一个很大很大的数组，数组中的每个元素就是一个字节(Byte),一个字节是8 位(Bit)，一个位的值要么是0要么是1。由此可见，计算机系统找元素的最小单位是字节，而不是位。

每种高级编程语言根都有其基本的数据类型，比如字符型、整型、布尔型，每种语言规定这些基本的数据类型占用的字节数可能都不一样。一个数据类型的占用的字节数称为字长。比如C语言规定某类型字长是4字节也就是32bit。

对于字长是多个字节的数据类型而言。表示该数据的这些字节，是按照正常的从左到右的方式放入数组中，还是倒过来把本来在最右边的字节放到最左边。正常的就是小端法放置，倒过来就是大端法放置，不同的机器放置的方法是不同的。如果你的程序要用到数据类型在底层的字节表示，那么程序在不同机器上运行的时候一定要小心，以免输出相反的字节信息。

指针由于用于指示该元素在大数组的哪个位置，相当于索引，索引的范围当然是越大越好，因此指针的位数和计算机的位数是一样的，也就是尽可能大，在32位机器上，索引的范围大约4Gb。也就是说该大数组最多能装下4Gb数据，再多就就没有索引可用了，而64位的机器索引范围要大得多，就可以配置很大的内存了。索引由于如果用2进制表示的，他显得很啰嗦很长，64位的机器，其索引有64位长。因此索引一般用16进制表示，以Ox开头表示16进制。

2 无符号整数

无符号整数在很多编程语言中是没有的，比如JAVA，但C语言有，如果你要做系统级的开发工作，也许会接触到。

2.1 无符号编码

对于程序员而言，我们面对的都是10进制的数据，而计算机都是二进制表示，所以必须要有一套标准，来实现他们之间的转换或者说映射。对于无符号数，有无符号的编码规则，他表明了一个无符号的二进制数表示为10进制的方式：

无符号编码

B表示binary，U表示usigned，2表示to，x表示该二进制数X的每一个位。
用这个无符号编码可以方便的将一个无符号二进制编码，转换位无符号的10进制。

那么反过来，无符号的10进制的到二进制有没有一个这样的公式来表示呢？嗯，没有。我们只能用常用的除2取余来计算，遇到很大的数时，建议用计算机程序帮助你做转换。

2.2 无符号运算

2.2.1 位运算

包括
非~、与&、或|、异或^运算。他们都是位级的，因此将对一个无符号数的每一位执行。

2.2.2 逻辑运算

&&、||、！，他们是数据级别的运算。也就是该数据的10进制值的逻辑运算。

2.2.3 算术运算

• 无符号加法和减法：就和进制加法和减法一样，没什么特别。
• 无符号乘法和除法：也和10进制的乘法和除法一样，只不过由于除法可能会出现小数，但会最终结果将仍然是整数，因为会发生舍入。对于无符号乘法和除法的时候，当乘以2的幂或除以2的幂时，可以用移位来进行。另外如果乘以任意常数而不是2的幂时，可以将该常数分解为几个2的幂相加，因此如果乘以任意常数，可以通过几个移位操作和加法操作来代替乘法操作。但除法无法实行这个转换。具体该使用移位还是使用乘法指令，需要更具具体情况确定。乘法指令往往要比加法和移位指令消耗更多的时钟周期。

3 有符号数

3.1 有符号数编码方式：补码

有符号数除了可以表示正数还可以表示负数。对于同样的位数例如8位，他将会以最高位来表示符号。0表示整数，1表示符数。同样都是8位因此和无符号数表示的数据个数是一样多的，但是范围不一样。0开头的数和1开头的数各占一半，但是全零是非负数。因此能表示的正数个数比负数个数要少一个，0既不是正数也不是负数。

补码编码给出了如何将一个二进制的补码转换为10进制的符号数：

符号数的补码编码

符号数的编码方式和无符号数编码的唯一区别在于最高位的权重是 负值

同样的，我们怎么把一个10进制的数变成二进制的数呢？有公式吗？没有。对于将10进制的数用补码表示的时候分两种情况：
正数转换为补码：
  1. 将其转换为二进制表示
  2. 在最高位补零
负数转换为补码：
  1.将求其对应正数的补码
  2.再求反码
  2.再加1
是麻烦了一点。

3.2 有符号数的运算

有符号数和无符号数的运算是一样的，计算机机器级指令不会区分有符号和无符号

3.3 有符号和无符号之间的转换

由于有符号和无符号之间在计算机底层是不会区分的。只要在高级语言层上才有区别。因此他们之间做强制类型转换时在位模式上是不会有变化的，而只改变了其表示成10进制的方法(即一个用无符号编码，一个用补码)

4 浮点数

4.1 浮点数的编码方式

浮点数的编码方式和整数的不一样，浮点数的表示相当于科学计数法表示，而写编码分为四种情况，就如同分段函数一样，所以来，跟我一块看看，浮点数怎么编码

浮点数编码公式

该公式展示了如何将一个二进制的浮点数转换位10进制的浮点数，我们只需要知道该浮点数的SME分别取值为多少就了。而该取值与浮点数二进制本身的位级表示有关，其32位和64位的表示分别如下：

32位机器浮点数位级结构

64位机器浮点数位级结构

可以看到，位级表示有三个部分：
s(符号位)：1表示负数0表示正数
exp(指数部分)：该部分是无符号表示的
frac(小数部分)：该部分实际上是小数，只是把小数点前面的0去掉了，实际上是(0.frac)
上述的位级表述除了有S之外，M和E并没有表示出来，那么他到底和exp(指数部分)和frac(小数部分)有什么关系呢？其之间的关系会更具指数部分的形式不同而不同，因此就分为了四种情况，也是IEEE的标准。

1. 规格化数。规格化数是指数部分既不是全0也不是全1的数。此时SME之间的转换关系为：

S = s；M = 1+0.f；E = exp-Bias
Bias = 2^k-1
k为exp部分的位数，32位时位8，64位时为11
exp是无符号编码

2. 非规格化数。非规格数指数部分全为0，非规格数可以将0表示为正0和负0，他们有不同的用途。SME的计算公式为：

S = s；M = 0.f；E = 1-Bias
Bias = 2^k-1
k为exp部分的位数，32位时位8，64位时为11
exp按理应该是0，但是为了光滑过度到别的类型数据，而取了1

3. 无穷大。指数部分全为1，同时小数部分全为0的数据。此时SME没有计算公式了，s=1的时候是负无穷，s=0的时候是正无穷。
4. NaN。空值，指数部分全为1，小数部分不为0.

可以看到浮点数转化为10进制数据是比较麻烦的，需要分情况换算。非规格化数据最靠近零，其次是规格化数据，再其次是无穷。

同样，如果想将10进制的数，转化为2进制的浮点数表示怎么做呢？比如10.24。首先你要将其换算成定点表示的小数，例如1010.101101然后表示成1.010101101x2³。接下来再一步一步根据指数的取值逆运算得到2进制浮点表示。相对来说，更加麻烦。最好不要手工操作。

4.2 浮点数的运算

我们知道，整数的运算我们可以手工操作，正常和10进制的数一样加减乘除就可以了。但我们看到浮点数如果这样做的话，就不行，比如1.1-1.1，就不等于0。因为浮点数其实他更像是源码表示，就是正数和负数，除了符号位不同，其他都相同。所以估计他有自己的一套源码的运算法则。不管是做整数的运算还是浮点数的运算，由于是在计算机中有限的位上进行，就会产生溢出，所以一些比如交换律、结合律、分配律可能不适用了。(a+b)+c和a+(b+c)可能就会产生不一样的结果。

4.3 舍入

浮点运算舍入时候，第一先向最近的值舍入，如果有两个最近的值，向偶数舍入，即使得最低有效位为偶数，0为偶数1为奇数。注意不是四舍五入。比如2.5他离2和3一样近，但他舍入到2会使得最低有效位2是偶数，因此2.5会向2舍入。