K-means聚类算法、Pandas绘制概率密度图和TSNE展示聚类结果

K-means聚类算法是典型的基于距离的非层次聚类算法，在最小化误差函数的基础上将数据划分为预定的K个类，使得K个类达到类内数据距离之和最小而类间距离之和最大。它是无监督学习算法，采用距离作为相似性的度量指标，即认为两个对象距离越近，其相似性就越大。
1、数据类型与相似性度量
(1)连续属性和离散属性数据
对于连续属性，要依次对每个属性的属性值进行零-均值化处理；对于离散属性，要依次对每个属性的属性值进行数值化处理。然后通过计算距离来度量相似性，K-means聚类算法中一般需要计算样本间的距离，样本和簇的距离，簇和簇的距离。其中，样本间的距离通常用欧式距离(欧几里得距离)、曼哈顿距离和闵可夫斯基距离，样本和簇的距离可以用样本到簇中心的距离代替，簇和簇距离可以用簇中心到簇中心的距离代替。
假定有n个样本，每个样本有p个属性，则可得如下数据矩阵：

设1 则可计算如下距离。

欧几里得距离：

曼哈顿距离：

闵可夫斯基距离：

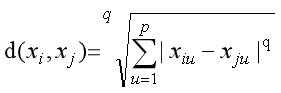
可见当q=1时，闵可夫斯基距离就是曼哈顿距离，当q=2时，闵可夫斯基距离就是欧氏距离。

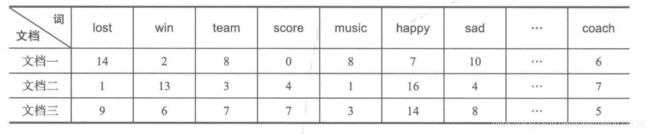
(2)文档数据
对于文档数据采用余弦相似性度量，首先统计文档中重要的词汇出现的频数，然后将文档数据整理成文档—词矩阵格式，如下所示：

两个文档间的相似性计算公式：
(按行将每个文档生成为一个向量，则可得两个向量间的余弦)

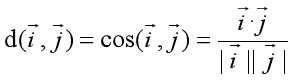
2、目标函数
使用误差平方和(Sum of Squared Error)来度量聚类的质量，对于多种聚类结果总是选择误差平方和最小的。
符号说明：

连续属性与离散属性数据的SSE：
(两个样本越相似，距离就越小，即误差就越小，所以用距离来代替误差)

文档数据的SSE：
(同理，可用余弦来代替误差)

3、算法流程
(1)从N个数据样本中随机选取K个样本作为初始的聚类中心。
(2)分别计算每个样本到K个聚类中心的距离，将样本归入到与聚类中心距离最近的聚类中。
(3)所有的样本都归入完毕后，重新计算聚类中心。对于连续属性，取每个属性的属性值的均值；对于离散属性，取每个属性的属性值的众数，这样就可以得到每个聚类的聚类中心。
(4)将重新计算的聚类中心与前一次计算的聚类中心比较，如果聚类中心发生变化，则转到步骤(2)，否则转步骤(5)。
(5)当聚类中心不发生变化时停止迭代并输出聚类结果。

例1：对餐饮客户的消费行为特征数据进行聚类，分析这些客户群的价值。

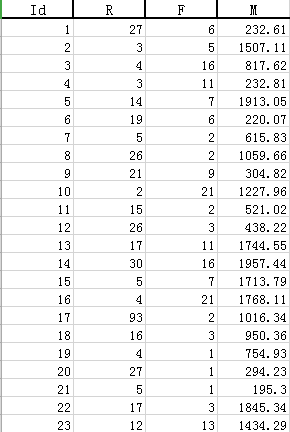
部分餐饮客户的消费行为特征数据表如下：
(R代表最近一次消费时间间隔，F代表消费频率，M消费总金额)

代码：

# -*- coding: utf-8 -*-
# 使用K-Means算法聚类消费行为特征数据

import pandas as pd

# 参数初始化
input_path = 'F:/DataMining/chapter5/consumption_data.xls'  # 销量及其他属性数据
output_path = 'F:/DataMining/chapter5/tmp/data_type.xls'  # 保存结果的文件名
k = 3  # 聚类的类别
iteration = 500  # 聚类最大迭代次数
data = pd.read_excel(input_path, index_col='Id')  # 读取数据
print('data: \n', data)
print('means: \n', data.mean())
print('stds: \n', data.std())
data_zs = 1.0*(data - data.mean())/data.std()  # 数据标准化

from sklearn.cluster import KMeans
model = KMeans(n_clusters=k, n_jobs=1, max_iter=iteration)  # 分为k类，n_jobs=1即不并发执行
model.fit(data_zs)  # 开始聚类
print('labels: \n', model.labels_)
print('cluster_centers_: \n', model.cluster_centers_)

# 简单打印结果
r1 = pd.Series(model.labels_).value_counts()  # 将数组格式的labels转换为Series格式再统计各个类别的数目
# r1.index = ['a', 'b', 'c']
print('r1: \n', r1)
r2 = pd.DataFrame(model.cluster_centers_)  # 将二维数组格式的cluster_centers_转换为DataFrame格式
print('r2: \n', r2)
r = pd.concat([r2, r1], axis=1)  # 横向拼接接(0是纵向),将r1变成一列拼接在r2的最右边，所有拼接的列的列名默认从0开始
r.columns = data.columns.tolist() + ['类别数目']  # 重命名表头
print('r: \n', r)

# 详细输出原始数据及其类别
output_data = pd.concat([data, pd.Series(model.labels_, index=data.index)], axis=1)   # 详细输出每个样本对应的类别
output_data.columns = list(data.columns) + ['聚类类别']  # 重命名表头
# output_data.to_excel(output_path)  # 保存结果

# pands绘制密度概率图
def density_plot(data): 
    import matplotlib.pyplot as plt
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
    # subplots=True表示dataframe格式的数据中每一列绘制一幅子图
    p = data.plot(kind='kde', linewidth=2,  subplots=True, sharex=False)
    # p[1]代表第1个子图
    [p[i].set_ylabel(u'密度') for i in range(k)]
    plt.legend()
    return plt

for i in range(k):
    density_plot(data[output_data['聚类类别'] == i]).show()

结果如下：
(这里只展示聚类1的结果)

聚类1人群的消费特征：消费时间间隔主要在40~80天，消费频率在0 ~15次，消费金额为0 ~2000元。

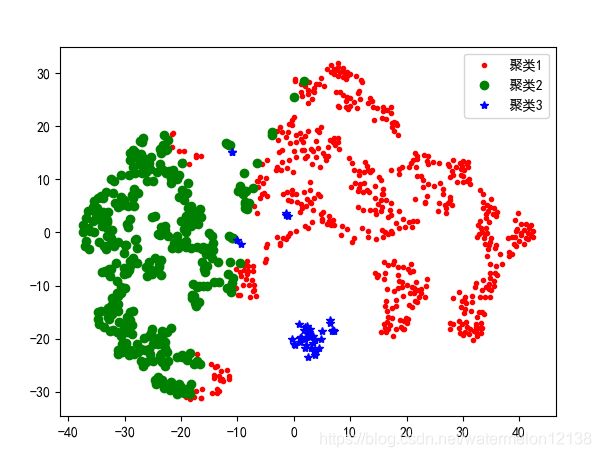
例2：使用TSNE进行数据降维并展示聚类结果
(使用TSNE展示例1中的聚类结果)

# -*- coding: utf-8 -*-
# 使用K-Means算法聚类消费行为特征数据

import pandas as pd

# 参数初始化
input_path = 'F:/DataMining/chapter5/consumption_data.xls'  # 销量及其他属性数据
output_path = 'F:/DataMining/chapter5/tmp/data_type.xls'  # 保存结果的文件名
k = 3  # 聚类的类别
iteration = 500  # 聚类最大迭代次数
data = pd.read_excel(input_path, index_col='Id')  # 读取数据
print('data: \n', data)
print('means: \n', data.mean())
print('stds: \n', data.std())
data_zs = 1.0*(data - data.mean())/data.std()  # 数据标准化

from sklearn.cluster import KMeans
model = KMeans(n_clusters=k, n_jobs=1, max_iter=iteration)  # 分为k类，n_jobs=1即不并发执行
model.fit(data_zs)  # 开始聚类
print('labels: \n', model.labels_)
print('cluster_centers_: \n', model.cluster_centers_)

# 简单打印结果
r1 = pd.Series(model.labels_).value_counts()  # 将数组格式的labels转换为Series格式再统计各个类别的数目
# r1.index = ['a', 'b', 'c']
print('r1: \n', r1)
r2 = pd.DataFrame(model.cluster_centers_)  # 将二维数组格式的cluster_centers_转换为DataFrame格式
print('r2: \n', r2)
r = pd.concat([r2, r1], axis=1)  # 横向拼接接(0是纵向),将r1变成一列拼接在r2的最右边，所有拼接的列的列名默认从0开始
r.columns = data.columns.tolist() + ['类别数目']  # 重命名表头
print('r: \n', r)

# 详细输出原始数据及其类别
output_data = pd.concat([data, pd.Series(model.labels_, index=data.index)], axis=1)   # 详细输出每个样本对应的类别
output_data.columns = list(data.columns) + ['聚类类别']  # 重命名表头
# output_data.to_excel(output_path)  # 保存结果

# 使用TSNE进行数据降维并展示聚类结果
from sklearn.manifold import TSNE
tsne = TSNE()
tsne.fit_transform(data_zs)  # 进行数据降维
# tsne.embedding_可以获得降维后的数据
print('tsne.embedding_: \n', tsne.embedding_)
tsn = pd.DataFrame(tsne.embedding_, index=data.index)  # 转换数据格式
print('tsne: \n', tsne)

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 不同类别用不同颜色和样式绘图
color_style = ['r.', 'go', 'b*']
for i in range(k):
    d = tsn[output_data[u'聚类类别'] == i]
    # dataframe格式的数据经过切片之后可以通过d[i]来得到第i列数据
    plt.plot(d[0], d[1], color_style[i], label='聚类' + str(i+1))
plt.legend()
plt.show()

结果展示：