快速沃尔什变换 FWT 学习笔记【多项式】

〇、前言

欢迎到我的 Wordpress 博客查看

之前看到异或就担心是 FWT，然后才开始想别的。

这次学了 FWT 以后，以后判断应该就很快了吧？

参考资料

• FWT 详解 知识点 by neither_nor
• 集训队论文 2015 集合幂级数的性质与应用及其快速算法 by 吕凯风

一、FWT 是什么

FWT 是快速沃尔什变换。它和快速傅里叶变换一样，原本都用于物理中的频谱分析。

但是由于它可分治的特点，在算法竞赛中常被用来计算位运算卷积。

二、FWT 能干什么

它可以在 $O(n\log n)$ 的时间复杂度内由数组 $a,b$ 得到数组 $c$，满足
$$\forall i\in [0,n)c_i=\sum _{j\oplus k=i}{a}_j\times b_k$$
其中 $\oplus$ 可以代表“与”，“或”，“异或”中的任意一种运算。

这叫做位运算卷积。

三、与、或卷积

我们需要把 $a,b$ 数组分别转化为 $a^{\prime },b^{\prime }$ 来通过一次乘法解决多个乘法问题。

对于或，我们有：若 $j\mathrm{o}\mathrm{r}i=i,k\mathrm{o}\mathrm{r}i=i$ 则 $(j\mathrm{o}\mathrm{r}k)\mathrm{o}\mathrm{r}i=i$。

虽然这样看上去和题目要求还差了一点，但是我们如果这样想呢：

构造数组 $a^{\prime },b^{\prime }$，
$$\begin{gathered} a_i^{\prime }=\sum _{j\mathrm{o}\mathrm{r}i=i}{a}_j \\ {b}_i^{\prime }=\sum _{k\mathrm{o}\mathrm{r}i=i}{b}_k \end{gathered}$$
即通过正变换由 $a$ 转化为 $a^{\prime }$，由 $b$ 转化为 $b^{\prime }$，

那么
$$\begin{array}{rl}{c}_i^{\prime }& =a_i^{\prime }\times b_i^{\prime }\\ & =\sum _{j\mathrm{o}\mathrm{r}i=i}{a}_j\sum _{k\mathrm{o}\mathrm{r}i=i}{b}_k\\ & =\sum _{j\mathrm{o}\mathrm{r}i=i}\sum _{k\mathrm{o}\mathrm{r}i=i}{a}_j{b}_k\\ & =\sum _{(j\mathrm{o}\mathrm{r}k)\mathrm{o}\mathrm{r}i=i}{a}_j{b}_k\end{array}$$
$(j\mathrm{o}\mathrm{r}k)\mathrm{o}\mathrm{r}i=i$ 就又是变换完的形式了。

再通过逆变换由 $c^{\prime }$ 转化回 $c$，那么 $c$ 就是满足 $c_i={\sum }_{j\mathrm{o}\mathrm{r}k=i}{a}_j{b}_k$ 的结果了。

同理，由于与运算满足：若 $j\mathrm{a}\mathrm{n}\mathrm{d}i=i$，$k\mathrm{a}\mathrm{n}\mathrm{d}i=i$，则 $(j\mathrm{a}\mathrm{n}\mathrm{d}k)\mathrm{a}\mathrm{n}\mathrm{d}i=i$。

因此和上面的变换是一样的。

现在我们需要找出 $a\to a^{\prime }$ 是怎么实现的。

正变换

针对或变换的举例：
$$\forall i\in [0,n)a_i^{\prime }=\sum _{j\mathrm{o}\mathrm{r}i=i}{a}_i$$
我们可以按位分治。从下到上转移，第 $i$ 层的状态 $j$ 用 $f[i,j]$ 表示所有比 $i$ 高的位与 $j$ 相同的状态 $k$ 的和。即
$$f[i,j]=\sum _{\lfloor \frac{k}{2^i}\rfloor =\lfloor \frac{j}{2^i}\rfloor ,k\mathrm{o}\mathrm{r}j=j}{a}_k$$
其中 $\lfloor \frac{k}{2^i}\rfloor$ 表示将 $k$ 在二进制下右移 $i$ 位。

如果还不好理解，那么对于 $f[5,1011001110_{(2)}]$，满足条件的 $k$ 是
$$\begin{gathered} i=5 \\ \begin{array}{rl}j& =1011001110\\ k& =1011000000\mathrm{o}\mathrm{r}x\end{array} \end{gathered}$$
其中的 $x$ 满足 $x\mathrm{o}\mathrm{r}001110=001110$。$k$ 必须满足在第 $5\sim 9$ 位与 $j$ 相同。

分析方程，会发现我们是可以利用 $f[i-1]$ 的信息的。在 $f[i-1,j]$ 中的每一个状态所存的 $\sum a_k$，$j$ 与 $k$ 从第 $i$ 位到最高位都是相等的，现在我们用到了第 $i$ 位，那么就考虑第 $i$ 位的取值。

就有了简洁的状态转移，令 $j$ 的第 $i$ 位是 $0$
$$\begin{array}{rl}f[i,j]& =f[i-1,j],\\ f[i,j+2^i]& =f[i-1,j]+f[i-1,j+2^i]\end{array}$$
所以 $a^{\prime }=f[\lceil \log n\rceil ]$，答案就是最上面一层。

同理，与的正变换的方程恰好反过来了
$$\begin{array}{rl}f[i,j]& =f[i-1,j]+f[i-1,j+2^i],\\ f[i,j+2^i]& =f[i-1,j+2^i]\end{array}$$

逆变换

逆变换是由 $f[i]$ 推 $f[i-1]$ 的过程。

直接由上面的式子倒过来就可以了。

或：
$$\begin{array}{rl}f[i,j]& =f[i+1,j],\\ f[i,j+2^i]& =f[i+1,j+2^i]-f[i+1,j]\end{array}$$
与：
$$\begin{array}{rl}f[i,j]& =f[i+1,j]-f[i+1,j+2^i],\\ f[i,j+2^i]& =f[i+1,j+2^i]\end{array}$$
因此卷积的答案最后就存在 $f[1,i]={\sum }_{j\oplus k=i}{a}_j{b}_k$ 里了。

四、异或卷积

这个东西有点麻烦，仍然需要构造。

定义运算 $x\otimes y=\mathrm{popcount}(x\mathrm{a}\mathrm{n}\mathrm{d}y)\mathrm{m}\mathrm{o}\mathrm{d}2$，称之为 $x$ 与 $y$ 的奇偶性。

它是一个满足 $(i\otimes j)\mathrm{x}\mathrm{o}\mathrm{r}(i\otimes k)=i\otimes (j\mathrm{x}\mathrm{o}\mathrm{r}k)$ 的运算，所以可以用来做异或卷积。

构造
$$\begin{gathered} a_i^{\prime }=\sum _{i\otimes j=0}{a}_j-\sum _{i\otimes j=1}{a}_j \\ {b}_i^{\prime }=\sum _{i\otimes k=0}{b}_k-\sum _{i\otimes k=1}{b}_k \end{gathered}$$
则
$$\begin{array}{rl}{c}_i^{\prime }& =\sum _{i\otimes j=0}{a}_j\sum _{i\otimes k=0}{b}_k-\sum _{i\otimes j=0}{a}_j\sum _{i\otimes k=1}{b}_k-\sum _{i\otimes j=1}{a}_j\sum _{i\otimes k=0}{b}_k+\sum _{i\otimes j=1}{a}_j\sum _{i\otimes k=1}{b}_k\\ & =\sum _{i\otimes (j\mathrm{x}\mathrm{o}\mathrm{r}k)=0}{a}_j{b}_k-\sum _{i\otimes (j\mathrm{x}\mathrm{o}\mathrm{r}k)=1}{a}_j{b}_k\end{array}$$
解释：式子中的第一行，第一项和第四项构成了 $i\otimes (j\mathrm{x}\mathrm{o}\mathrm{r}k)=0$ 的全部可能性：$00$ 和 $11$；第二项和第三项构成了 $i\otimes (j\mathrm{x}\mathrm{o}\mathrm{r}k)=1$ 的全部可能性：$01$ 和 $10$。所以可以写 $\sum$，而且由于每项不相交，所以不能乘 $2$。

可以发现 $c^{\prime }$ 也是一个变换完了的式子，把它逆变换回去就可以了。

正变换

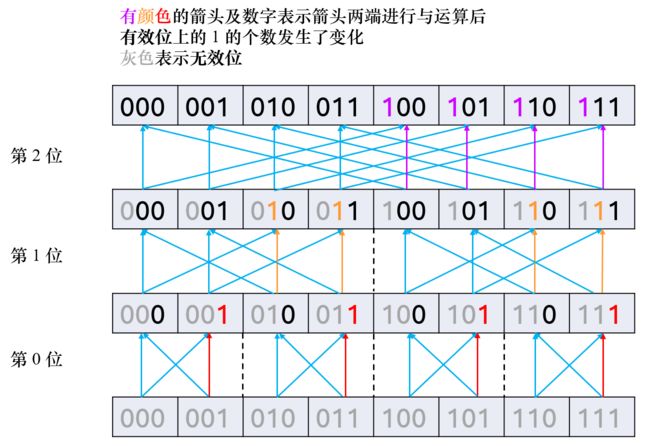
仍然按位分治，同样考虑上面那样逐位转移。

在枚举第 $i$ 位的不同时，状态 $j$ 和状态 $j+2^i$ 都可以从第 $i-1$ 层的 $j$ 和 $j+2^i$ 转移过来。其中 $j$ 的第 $i$ 位为 $0$。

这样的话有四种情况：

• $[i,j]\leftarrow [i-1,j]$，$(0\mathrm{a}\mathrm{n}\mathrm{d}0)$ 是不变的；
• $[i,j]\leftarrow [i-1,j+2^i]$，$(0\mathrm{a}\mathrm{n}\mathrm{d}1)$ 是不变的；
• $[i,j+2^i]\leftarrow [i-1,j]$，$(1\mathrm{a}\mathrm{n}\mathrm{d}0)$ 是不变的；
• $[i,j+2^i]\leftarrow [i-1,j+2^i]$，$(1\mathrm{a}\mathrm{n}\mathrm{d}1)$ 会改变。

这个图中蓝色（无色）的箭头表示正转移，其他颜色的箭头表示负转移。

也就是说，转移之后，这个状态内部的全部元素进行 $\otimes$ 的结果都从 $0$ 变成了 $1$ 或从 $1$ 变成了 $0$。

那么在最终结果方面就会产生影响，因此那些转移我们把它定为负的。

还有一种理解方法。因为最上面一行是我们正变换的结果，可以通过这个图从上到下来看出它的贡献来源。

从 $a_i^{\prime }$ 出发，遇到有颜色的边，就要把子数内的贡献取反（$\times -1$），它的意义也是 $k\otimes i=\neg (k\otimes i)$。

这样对每一个位置就可以满足
$$f[i,j]=\sum _{k\otimes j=0}{a}_k-\sum _{k\otimes j=1}{a}_k$$
了。其中 $k$ 只枚举了有效位。

观察图可以发现，状态转移方程是
$$\begin{array}{rl}f[i,j]& =f[i-1,j]+f[i-1,j+2^i],\\ f[i,j+2^i]& =f[i-1,j]-f[i-1,j+2^i]\end{array}$$

逆变换

把正变换上下相减，除以 $2$ 即可
$$\begin{array}{rl}f[i,j]& =\frac{f[i+1,j]+f[i+1,j+2^i]}{2},\\ f[i,j+2^i]& =\frac{f[i+1,j]-f[i+1,f[j+2^i]]}{2}\end{array}$$

五、代码

#include
#include
#define p 998244353
#define inv 499122177ll
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
int read()
{
    int x=0;
    char ch=gc();
    while(ch<'0'||ch>'9')
        ch=gc();
    while(ch>='0'&&ch<='9')
    {
        x=x*10+(ch&15);
        ch=gc();
    }
    return x;
}
int A[1<<17],B[1<<17],a[1<<17],b[1<<17],n,tot;
void init()
{
    for(int i=0;i<(1<<n);++i)
    {
        a[i]=A[i];
        b[i]=B[i];
    }
}
void Or(int *f)
{
    for(int bs=2;bs<=tot;bs<<=1)
    {
        int g=(bs>>1);
        for(int i=0;i<tot;i+=bs)
            for(int j=0;j<g;++j)
                f[i+j+g]=(f[i+j]+f[i+j+g])%p;
    }
}
void iOr(int *f)
{
    for(int bs=tot;bs>=2;bs>>=1)
    {
        int g=(bs>>1);
        for(int i=0;i<tot;i+=bs)
            for(int j=0;j<g;++j)
                f[i+j+g]=(f[i+j+g]+p-f[i+j])%p;
    }
}
void And(int *f)
{
    for(int bs=2;bs<=tot;bs<<=1)
    {
        int g=(bs>>1);
        for(int i=0;i<tot;i+=bs)
            for(int j=0;j<g;++j)
                f[i+j]=(f[i+j]+f[i+j+g])%p;
    }
}
void iAnd(int *f)
{
    for(int bs=tot;bs>=2;bs>>=1)
    {
        int g=(bs>>1);
        for(int i=0;i<tot;i+=bs)
            for(int j=0;j<g;++j)
                f[i+j]=(f[i+j]+p-f[i+j+g])%p;
    }
}
void Xor(int *f)
{
    for(int bs=2;bs<=tot;bs<<=1)
    {
        int g=(bs>>1);
        for(int i=0;i<tot;i+=bs)
            for(int j=0;j<g;++j)
            {
                int t0=(f[i+j]+f[i+j+g])%p,t1=(f[i+j]+p-f[i+j+g])%p;
                f[i+j]=t0;
                f[i+j+g]=t1;
            }
    }
}
void iXor(int *f)
{
    for(int bs=tot;bs>=2;bs>>=1)
    {
        int g=(bs>>1);
        for(int i=0;i<tot;i+=bs)
            for(int j=0;j<g;++j)
            {
                int t0=inv*(f[i+j]+f[i+j+g])%p,t1=inv*(f[i+j]+p-f[i+j+g])%p;
                f[i+j]=t0;
                f[i+j+g]=t1;
            }
    }
}
int main()
{
    #ifdef wjyyy
        freopen("a.in","r",stdin);
    #endif
    n=read();
    tot=(1<<n);
    for(int i=0;i<tot;++i)
        A[i]=read();
    for(int i=0;i<tot;++i)
        B[i]=read();
    init();
    Or(a);
    Or(b);
    for(int i=0;i<tot;++i)
        a[i]=(long long)a[i]*b[i]%p;
    iOr(a);
    for(int i=0;i<tot;++i)
        printf("%d ",a[i]);
    puts("");
    init();
    And(a);
    And(b);
    for(int i=0;i<tot;++i)
        a[i]=(long long)a[i]*b[i]%p;
    iAnd(a);
    for(int i=0;i<tot;++i)
        printf("%d ",a[i]);
    puts("");
    init();
    Xor(a);
    Xor(b);
    for(int i=0;i<tot;++i)
        a[i]=(long long)a[i]*b[i]%p;
    iXor(a);
    for(int i=0;i<tot;++i)
        printf("%d ",a[i]);
    return 0;
}