POJ 3525 || Most Distant Point from the Sea (凸包求最大内接圆，半平面交内推r

题目在问这样一个问题：给定一个凸多边形，找到其中的一个点，使得其到每条边的距离最小值最大，输出这个距离。

其实就是在问你，这个多边形中最大的一个内切圆有多大。

怎么做呢？如果我们事先知道一个半径R，我们是不是能验证这个R是否可行呢？

答案是肯定的，这样想：如果我们把这个多边形每条边都向内推进R，之后如果这个多边形还存在的话，就说明这个半径为R的圆肯定塞得下，因为还可以往里缩嘛。直到他们缩成一个点的时候，这个时候缩的距离就是我们要找的R了，同时这个点也肯定是我们要找的圆的圆心。

那么，我们就可以二分一下R，之后用半平面交判断一下多边形是否还在就行了。

半平面交的实现和求多边形的核一模一样，我们可以考虑这个问题是一堆半平面的交，实际上实现手段是切割已有的答案区域，得到一个更小的答案区域，这就是半平面交的实现手段。为此，我们一开始选择一个肯定要大一些的答案区域，再不断用直线去切割就可以了。

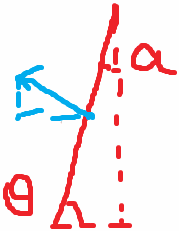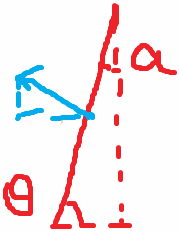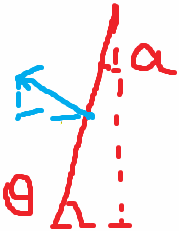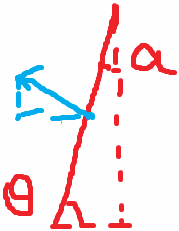
最想说一下什么呢？是“将每条边推进R”应该怎么实现。很多人绕了半天，实际上我找到一个很简单的公式：把直线表示成Ax + By + C = 0后（已考虑顺逆时针所带来的正负号问题），把直线向内推进d时，只需要写：

c += d * sqrt(a*a + b*b);

就可以了。

为什么呢？我们可以简单推导一下：

①当直线不垂直于X轴的时候，不妨假设直线向左上方移动（直线方向为右上）：

有如下关系成立：

tanθ = k = - A / B

sinα = -B / sqrt( a*a + b*b)

cosα = A / sqrt(a*a + b*b)

dx = d*cosα

dy = d*sinα

新直线方程为A（x+dx） + B（y+dy） + C = 0

拆开整理，会发现分子上面有一个A² + B² ，和下面的sqrt（A² + B²） 约掉一份，得出△C = d* sqrt（A² + B²）。

②当直线垂直于X轴的时候，解析式为Ax + C = 0， 不妨假设直线向左移动（其方向是向上的），则新直线为A（x + d）+ C =0, 于是有△C = Ad = d * sqrt（a*a+b*b）。

所以，以后遇到推进类问题的时候，只需要先求出ABC，再修改一个C，就可以得到推进之后的直线了。

#include
#include
#include
#include
#include
#define D(x) cout<<#x<<" "<0)
		return 1;
	return -1;
}

struct Point
{
	double x,y;
	Point(){}
	Point(double _x,double _y)
	{
		x = _x;y = _y;
	}
	Point operator -(const Point &b)const
	{
		return Point(x - b.x,y - b.y);
	}
	//叉积
	double operator ^(const Point &b)const
	{
		return x*b.y - y*b.x;
	}
	//点积
	double operator *(const Point &b)const
	{
		return x*b.x + y*b.y;
	}
	//绕原点旋转角度B（弧度值），后x,y的变化
	void transXY(double B)
	{
		double tx = x,ty = y;
		x = tx*cos(B) - ty*sin(B);
		y = tx*sin(B) + ty*cos(B);
	}
};

Point ori[150];
Point kernel[150];
int p_kernel = 0;

Point tp[150];

int n;

void getLine(Point p1,Point p2,double &a,double &b,double &c)
{
	a = p2.y - p1.y;
	b = p1.x - p2.x;
	c = p2.x*p1.y - p1.x*p2.y;
	return;
}

Point Intersection(Point p1,Point p2,double a,double b,double c)
{
	double u = fabs(a*p1.x + b*p1.y + c);
	double v = fabs(a*p2.x + b*p2.y + c);
	Point t;
	t.x = (p1.x*v + p2.x*u)/(u+v);
	t.y = (p1.y*v + p2.y*u)/(u+v);
	return t;
}

void cut(double a,double b,double c,Point p[],int &cnt)
{
	int tmp = 0;
	for(int i = 1;i <= cnt;i++)
	{
		//当前点在左侧，逆时针的点
		if(a*p[i].x + b*p[i].y + c < EPS)
			tp[++tmp] = p[i];
	else
	{
		if(a*p[i-1].x + b*p[i-1].y + c < -EPS)
			tp[++tmp] = Intersection(p[i-1],p[i],a,b,c);
		if(a*p[i+1].x + b*p[i+1].y + c < -EPS)
			tp[++tmp] = Intersection(p[i],p[i+1],a,b,c);
		}
	}
	
	for(int i = 1;i <= tmp;i++)
		p[i] = tp[i];
	p[0] = p[tmp];
	p[tmp+1] = p[1];
	cnt = tmp;
	return;
}

void init()
{
	memset(ori, 0, sizeof(ori));
	memset(kernel, 0, sizeof(kernel));
	p_kernel = 0;
	return;
}

int main()
{
	while(true)
	{
		scanf("%d", &n);
		if(n==0)
			break;
		
		init();
		int i;
		for(i=1; i<=n;i++)
		{
			scanf("%lf %lf", &ori[i].x, &ori[i].y);
		}
		
		ori[0] = ori[n];
		ori[n+1] = ori[1];
		
		double low = 0, high = INF;
		while(fabs(high - low) > 1e-5)
		{
			double mid = (high+low) /2;
				
			for(i=0; i<=n+1;i++)
				kernel[i] = ori[i];
			p_kernel = n;
			
			for(i=1; i<=n;i++)
			{
				double a,b,c;
				getLine(ori[i], ori[i+1], a, b, c);
				
				c += mid * sqrt(a*a + b*b);
				cut(a,b,c, kernel, p_kernel);
			}
			
		//	D(p_kernel);
			
			if(p_kernel > 0)
				low = mid;
			else
				high = mid;
		}
		
		printf("%lf\n", high);
	}
	//system("pause");
	return 0;
}