AC自动机详解，很清楚

序

有些人说，学AC自动机没有必要先学kmp和trie树,但我认为，前置知识是很有必要的，毕竟，他们中有ac自动机的思想

ac自动机最重要的就是fail指针，跟kmp一样，我们要优化它，就不能只是失配后回到起点，重新匹配这样复杂度太高，所以我们用空间换时间，我这里所说的空间就是多维护的信息，时间就是复杂度，自己口胡的，大佬勿喷。于是，我们引入fail

指针来维护一下，最长后缀子串。下面开始用图学习ac自动机吧(个人比较喜欢放图,能用一张图解决的绝不叨叨)

正文

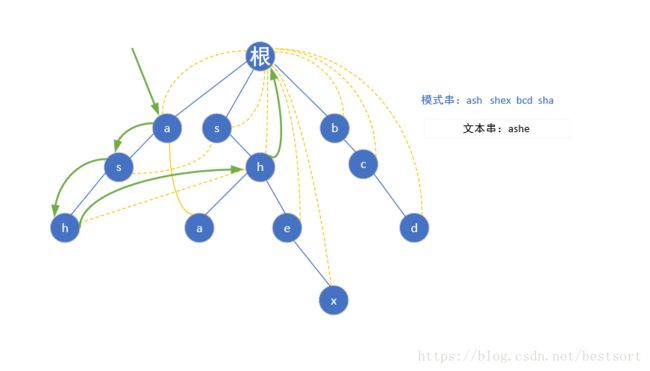
首先给定模式串"ash",“shex”,“bcd”,“sha”,然后我们根据模式串建立

如下trie树:

然后我们再了解下一步:

ac自动机,就是在tire树的基础上,增加一个fail指针,如果当前点匹配失败,则将指针转移到fail指针指向的地方,这样就不用回溯,而可以路匹配下去了.(当前模式串后缀和fail指针指向的模式串部分前缀相同,如

abce和bcd,我们找到c发现下一个要找的不是e,就跳到bcd中的c处,看看此处的下一个字符(d)是不是应该找的那一个)一般,fail指针的构建都是用bfs实现的

首先每个模式串的首字母肯定是指向根节点的(一个字母你瞎指什么指,指了也是头字母有什么用嘛)

现在第一层bfs遍历完了,开始第二层

(根节点为第0层)第二层a的子节点为s,但是我们还是要从a-z遍历,如果不存在这个子节点我们就让他指向根节点(如下图红色的a)

当我们遍历到s的时候,由于存在s这个节点,我们就让他的fail指针指向他父亲节点(a)的fail指针指向的那个节点(根)的具有相同字母的子节点(第一层的s),也就是这样

按照相同规律构建第二层后,到了第三层的h点,还是按照上面的规则,我们找到h的父亲节点(s)fail指针指向的那个位置(第一层的s)然后指向它所指向的相同字母根->s->h的这个链的h节点,如下图

然后匹配就很简单了,这里以ashe为例我们先用ash匹配,到h了发现:诶这里ash是一个完整的模式串,好的ans++,然后找下一个e,可是ash后面没字母了啊,我们就跳到hfail指针指向的那个h继续找,还是没有?再跳,结果当前的h指向的是根节点,又从

根节点找,然而还是没有找到e,程序END过程如下图

理解

首先我们让与根节点直接相连的节点的fail直接指向root,为了让你更好的理解fail指针，我们以节点x,y,z为例，我们让从图中我们可以看出x节点的fail指向了y节点，y节点的fail指向了z节点，为什么会这样指，

因为x节点表示字符串abc,而字典树中含有最长，且以c结尾，且是abc的后缀的字符串bc(以y节点结尾的），同理，以y节点表示的字符串是bc,而以c结尾，且是bc的后缀的最长字符串是c（以z节点结尾的）。这就是

fail指针指向的目标，那么我们得到了这个fail指针在匹配中有什么用呢，我们还是用上面的那个图来举例说明一下，假设文本串是abce,通过字典树我们可以看出，通过abc,所以我们可以匹配到x节点，但是到后

面，我们发现d与e不匹配，这时我们就需要用到当前节点的fail了，因为x的fail指向的是y节点，所以我们直接跳到y节点，这是发现y节点后面有e，匹配上了，所以单词bce就在文本串abce中被检测出来了。当然

这只是最简单的一种情况。
###回顾

重点我们再来自问自己一边，为什么要维护一个fail指针，好了吗我来说说我的观点，fail指针维护一个当前节点的最长后缀，（后缀不包括最前面的）为什么不维护最长前缀或这个序列本身呢，我们再来看一

下fail指针的使用时间，是当你匹配失败后，才使用，那么失败的原因是后面的一部分不匹配，我们的信息是从前面继承的，所以要维护离我们要维护的信息最近的信息，也就是后缀，但为了后面的匹配成功的几率尽

可能地大，所以我们每次后缀的长度减1（是较前面的减1），是不是很妙。

代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int maxn =  2*1e6+9;

int trie[maxn][26]; //字典树
int cntword[maxn];  //记录该单词出现次数
int fail[maxn];     //失败时的回溯指针
int cnt = 0;

void insertWords(string s){
    int root = 0;
    for(int i=0;iq;
    for(int i=0;i<26;i++){      //将第二层所有出现了的字母扔进队列
        if(trie[0][i]){
            fail[trie[0][i]] = 0;
            q.push(trie[0][i]);
        }
    }

//fail[now]    ->当前节点now的失败指针指向的地方
tire[now][i] -> 下一个字母为i+'a'的节点的下标为tire[now][i]
    while(!q.empty()){
        int now = q.front();
        q.pop();

        for(int i=0;i<26;i++){      //查询26个字母
            if(trie[now][i]){
                //如果有这个子节点为字母i+'a',则
//让这个节点的失败指针指向(((他父亲节点)的失败指针所指向的那个节点)的下一个节点)
                //有点绕,为了方便理解特意加了括号

                fail[trie[now][i]] = trie[fail[now]][i];
                q.push(trie[now][i]);
            }
            else//否则就让当前节点的这个子节点
                //指向当前节点fail指针的这个子节点
                trie[now][i] = trie[fail[now]][i];
        }
    }
}


int query(string s){
    int now = 0,ans = 0;
    for(int i=0;i> n;
    for(int i=0;i> s ;
        insertWords(s);
    }
    fail[0] = 0;
    getFail();
    cin >> s ;
    cout << query(s) << endl;
    return 0;
}