轮廓线dp概述

轮廓线dp是动态规划的一种（据说还叫插头dp），就直接上例题了吧：Mondriaan’s Dream

Mondriaan’s Dream

Time Limit: 3000MS
Memory Limit: 65536K
Total Submissions: 19038
Accepted: 10852

Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his ‘toilet series’ (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he’ll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won’t turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h h and the width w w of the large rectangle. Input is terminated by h=w=0 h = w = 0 . Otherwise, 1≤h,w≤11 1 ≤ h , w ≤ 11 .

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

Sample Output

1
0
1
2
3
5
144
51205

大概意思就是给你一个矩形，用1*2的小矩形把它填满，有多少种填法？

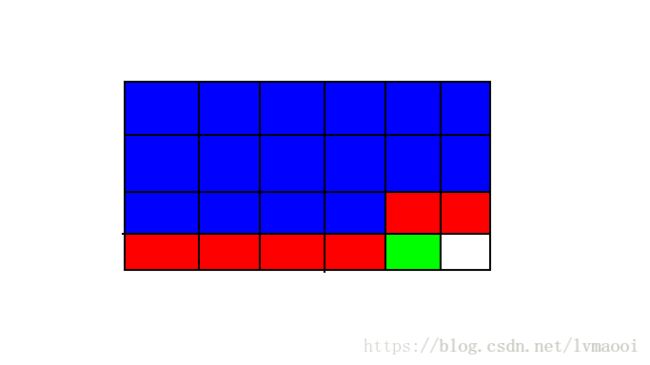
首先题目要满足这张图有一维比较小，可以进行状压，显然这道题是满足的，然后我们画个图分析一下：
假设我们从左到右从上到下填，现在已经填到绿色的方格了（以绿色为1*2格子的右下角，三种选择：1.不填 2.竖着填 3.横着填），显然蓝色的格子以后永远都不会被填到了，所以蓝色一定是被填完了的。而红色的有可能对之后填法产生影响，所以我们用一个状压记录红色格子是否被填。

我们由此想到状态表示： fi,j,k f i , j , k 表示填到第 i i 行第 j j 列（第 i i 行第 j j 列是绿色格子）时，红色部分填法为 k k 时的方案数。

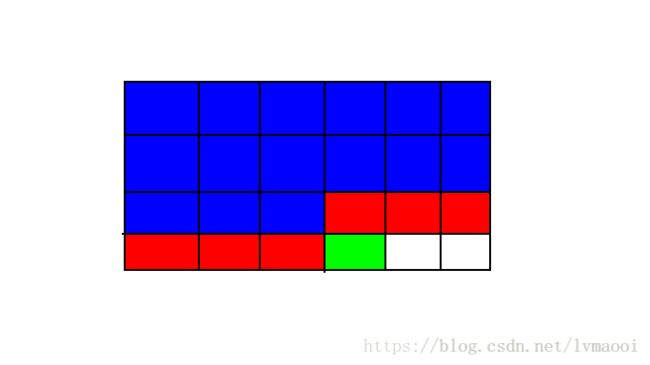
上面的图会转移成：

值得注意的是，红色并不是代表被覆盖过，而是记录成状态。

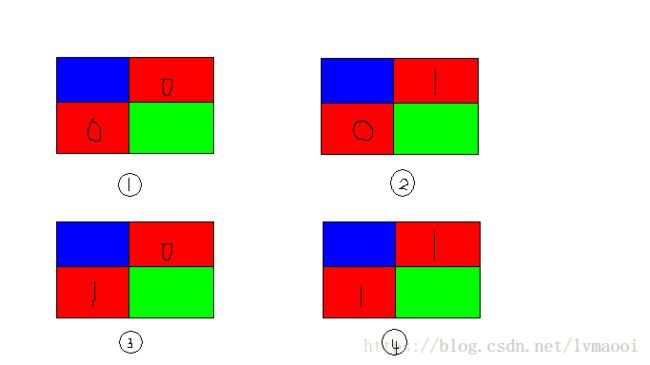
那么怎么转移呢？其实已经很明显了，我们再画一个图（0表示没有被覆盖，1表示被覆盖）：

1号：只能竖着填，因为绿色上面的红色必须要被覆盖，不然之后就不会被覆盖了。
2号：可以横着填，也可以不填。
3号：只能竖着填，同理，上面的这次不被覆盖就没有机会被覆盖了。
4号：只能不填，横竖都填不了。

然后我们就推出了状态转移方程。
初始状态为f(1,1,红色全部被填)=1。因为边界外是填不了的，就相当于被覆盖过了。还有注意每一排第一个是没有办法横着摆的。然后就没什么了，最后输出f（n+1，1，红色全部被填）就行。

然后附上代码：

#include
#include
#include
using namespace std;

long long f[2][2049];
int T;
int n,m,r;

int main()
{
    for(;;)
    {
      scanf("%d%d",&n,&m);
      if(n==0&&m==0) break;
      memset(f,0,sizeof(f));
      f[1][(1<1]=1;
      for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
          r=((i-1)*m+j)%2;
          for(int k=0;k<=(1<1;k++)
            f[r^1][k]=0;
          for(int k=0;k<=(1<1;k++)
          {
            if(j-1>0&&(k&(1<2))==0&&(k&(1<1))==(1<1)) f[r^1][k|(1<2)|(1<1)]+=f[r][k];
            if((k&(1<1))==0) f[r^1][k|(1<1)]+=f[r][k];
            if((k&(1<1))==(1<1)) f[r^1][k^(1<1)]+=f[r][k];
          }
        }
      printf("%lld\n",f[r^1][(1<1]);
    }
}