算法学习笔记(9)-回溯算法与八皇后问题

回溯算法也叫试探搜索算法，它是一种类似于暴力枚举的搜索方法, 但是不同的是在回溯的过程中存在剪枝和状态的自转化,所以对于暴力枚举类问题,往往选择使用回溯算法,以达到优化时间和空间的目的

一.用回溯算法解决问题的一般步骤

1、 针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。
2 、确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
3 、以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。

我们用八皇后问题来理解一下回溯算法的执行步骤:

二. 八皇后问题

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋盘上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

我们可以先解决这个问题的简化版本,即四皇后问题,四皇后问题指的是在4×4的国际象棋盘上摆放四个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

2.1 回溯思路

解决这个问题的思路是这样子的:

1.首先我们在棋盘的左下角摆放一个皇后,此时还有3个皇后要摆放
2.接下来我们在棋盘的第二行的某个位置摆放一个皇后,使其不会相互攻击;观察第三行是否可以摆放得下皇后,如果不可以则将该皇后挪到下一个可行的列
3.接下来在棋盘的第三行某个位置摆放一个皇后,使其不会相互攻击,观察第四行是否可以摆放得下皇后,如果不可以则将该皇后挪到下一个可行的列
4.接下来在棋盘的第四行某个位置摆放一个皇后,使其不会相互攻击,此时4个皇后摆放完毕,这是四皇后问题的一个解

其中2,3步中的"观察第三行是否可以摆放得下皇后"这个过程称之为"剪枝",即剪去了绝对不可能成立的情况;而"如果不可以则将该皇后挪到下一个可行的列"这个过程称之为"状态回溯",即将棋子重新放置,我画了一张图来表示这个过程:

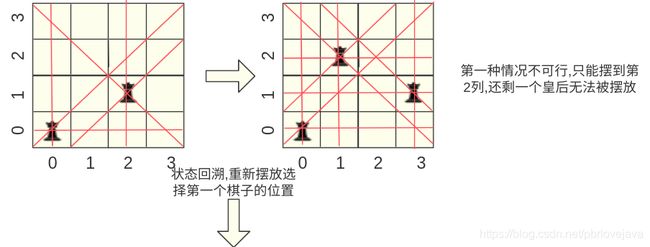
回溯的过程大致就是这样:不断地去寻找每一行可以放置棋子的位置,放置之后发现不行或者已经达到了4皇后的解,就将其撤回,重新寻找下一种摆放的可能.

2.2 代码解决

一般的回溯算法的模板是这样子的:

private void backtrace(int count) {
        //回溯终止条件
        if (count == xxx) {
           //进行记录处理
            return;
        }

        //回溯过程
        while(xx) {
      			//...
                //继续进行回溯调用
                backtrace(count + 1);
                //状态回溯
                //...
            }
        return;
    }

以下即为任意N皇后问题的解决代码:

    private int res;
    private int N;
    private int[] record;//记录放置的皇后位置
    public int totalNQueens(int n) {
        res = 0;
        N = n;
        record = new int[n];
        backtrace(0, 0);
        return res;
    }

    private void backtrace(int row, int count) {
        //回溯终止条件
        if (count == N) {
            res++;
            return;
        }

        //回溯过程
        //逐行向上放置皇后,可以避免同一行出现皇后,接下来只需要判断每一列的格子是否可以防止皇后
        for (int col = 0; col < N ; col++) {
            if (check(row, col)) {
                System.out.println("在第"+row+"行,第"+col+"列摆放第"+(count+1)+"个皇后");
                //放置皇后在row, col位置
                record[row] = col;
                //继续网上寻找放置皇后的位置
                backtrace(row + 1, count + 1);
                //状态回溯(撤回row, col位置的皇后)
                System.out.println("==撤回第"+row+"行,第"+col+"列的第"+(count+1)+"个皇后");
                record[row] = 0;
            }
        }
        return;
    }

    private boolean check(int row, int col) {
        for (int i = 0; i < row ; i++) {
            //判断列上有没有皇后
            if (record[i] == col) return false;
            //判断斜列上又没有皇后
            if (Math.abs(i - row) == Math.abs(record[i] - col)) return false;
        }
        return true;
    }

执行程序,即可获得4皇后问题的回溯过程和解数量了:

在第0行,第0列摆放第1个皇后
在第1行,第2列摆放第2个皇后
-----撤回第1行,第2列的第2个皇后
在第1行,第3列摆放第2个皇后
在第2行,第1列摆放第3个皇后
-----撤回第2行,第1列的第3个皇后
-----撤回第1行,第3列的第2个皇后
-----撤回第0行,第0列的第1个皇后
在第0行,第1列摆放第1个皇后
在第1行,第3列摆放第2个皇后
在第2行,第0列摆放第3个皇后
在第3行,第2列摆放第4个皇后
-----撤回第3行,第2列的第4个皇后
-----撤回第2行,第0列的第3个皇后
-----撤回第1行,第3列的第2个皇后
-----撤回第0行,第1列的第1个皇后
在第0行,第2列摆放第1个皇后
在第1行,第0列摆放第2个皇后
在第2行,第3列摆放第3个皇后
在第3行,第1列摆放第4个皇后
-----撤回第3行,第1列的第4个皇后
-----撤回第2行,第3列的第3个皇后
-----撤回第1行,第0列的第2个皇后
-----撤回第0行,第2列的第1个皇后
在第0行,第3列摆放第1个皇后
在第1行,第0列摆放第2个皇后
在第2行,第2列摆放第3个皇后
-----撤回第2行,第2列的第3个皇后
-----撤回第1行,第0列的第2个皇后
在第1行,第1列摆放第2个皇后
-----撤回第1行,第1列的第2个皇后
-----撤回第0行,第3列的第1个皇后
故一共有2个解