Java中数组冒泡排序、选择排序、二分查找的详细分析
前言:尽管在实际开发中,我们通过Arrays工具类就可以便利地对数组进行排序和查找的操作,但是掌握冒泡排序、选择排序、二分法查找的思想对于编程来说还是极其重要的,在很多场景都会用到。希望通过这篇博客的分析能给大家带来收获。
主题:数组的排序和查找
1、冒泡法排序:
需求:将数组 int arr = {2,4,11,0,-4,333,90} 通过冒泡法进行排序,下面以升序排列进行分析。
① 思路分析:
第1次比较:先让数组中的第1个元素和第2个元素进行比较,如果第1个元素的值如果比第2个元素的大,那么就交换位置。接着再让第2个元素和第3个元素进行比较...直到比到最后一个元素。第1次比较完,数组中的最大值就出现在数组最大索引处。
第2次比较:因为最大索引处已经放上了数组中的最大值,不需要再进行比较。再次让经过第1次比较后数组中的第1个元素和第2个元素比较,如果第1个元素的值如果比第2个元素的大,那么就交换位置...(重复第1次比较中的操作)。第2次比较完,数组中的第2大的值就出现在数组倒数第二个位置。
第3次比较、第4次比较、第5次比较、第6次比较都是同样的思路。
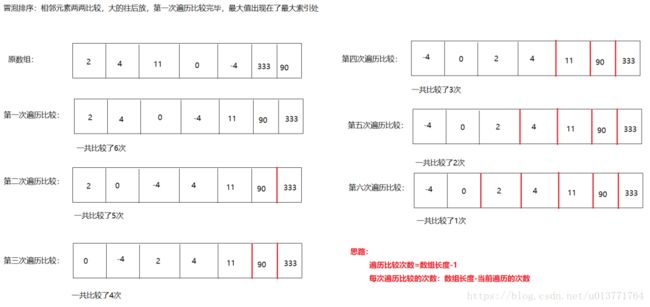
② 思路图解:
③ 光看思路图解可能还不详细,我们可以看看冒泡法的具体比较过程:
值得留意的细节是:数组中一共7个元素,共比较了6次,对应了外循环中 i 从 1 变化到 6(即7-1); 而每次比较的次数也在逐渐变少,对应着内循环中 j 从 0 变化到 arr.length - i(即第1次比较了6次,第2次比较了5次,第3次比较了4次...也就是第 i 次比较的次数是 7- i);
④ 代码实现:
/**
* 冒泡排序
* @param arr
* @param isAsc为true进行升序排列,为false进行降序排列
*/
public static void bubbleSort(int[] arr, boolean isAsc) {
// 遍历比较次数=数组长度-1
for (int i = 1; i < arr.length; i++) {
// 每次遍历比较的次数:数组长度-当前遍历的次数
for (int j = 0; j < arr.length - i; j++) {
if (isAsc) {
// 升序排列
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
} else {
// 降序排列
if (arr[j] < arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}//内循环
}//外循环
}//方法2、选择法排序
需求:将数组 int arr = {2,4,11,0,-4,333,90} 通过选择法进行排序,我们以降序排列进行分析。
① 思路分析:选择法和冒泡法排序的不同在于,选择法排序不是前后相邻元素进行比较,而是在每次比较中选定指定索引的数组元素和其余的元素进行比较。
第1次比较:先让数组中索引为1的元素和索引为2的元素进行比较,如果第1个元素的值如果比第2个元素的小,那么就交换位置。接着让索引为1的元素和索引为3的元素进行比较...直到比到数组中最后一个元素。第1次比较完,数组中的最大值出现在数组中索引为1的地方。
第2次比较:因为索引为1的地方已经放上了数组中的最大值,不需要再进行比较。第2次比较时,让经过第1次比较后数组索引为2的元素同索引为3的元素进行比较,如果第2个元素的值如果比第3个元素的小,那么就交换位置...(重复第1次比较中的操作)。第2次比较完,数组中的第2大的值就出现在数组中索引为2的位置。
第3次比较、第4次比较、第5次比较、第6次比较都是同样的思路。
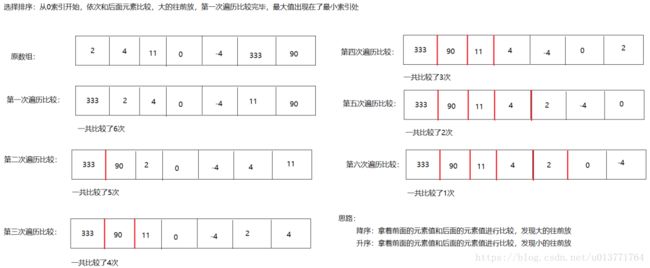
② 思路图解
③ 同样的,我们来看看具体的比较过程:
值得留意的细节是:数组中一共7个元素,同样比较了6次,对应了外循环中 i 从 0 变化到 5(即7-1-1); 而每次比较的次数也在逐渐变少,对应着内循环中 j 从 i +1 变化到 arr.length (即第1次比较的过程是选中的元素从第2个元素开始比较,比较了6次;第2次从第3个元素开始比较,比较了5次;第3次从第4个元素开始比较,比较了4次...也就是第 i 次比较是从第 i + 1个元素开始比较);
④ 代码实现
/**
* 选择排序
* @param arr
* @param isAsc为true进行升序排列,为false进行降序排列
*/
public static void selectSort(int[] arr, boolean isAsc) {
// 外面的循环是控制当前没有确定最值的索引
for (int i = 0; i < arr.length-1; i++) {
// 里面的循环是控制前面元素和剩余元素进行比较
for (int j = i+1; j < arr.length; j++) {
if (isAsc) {
// 升序:拿着前面的元素值和后面的元素值进行比较,发现小的往前放
if (arr[i] > arr[j]) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
} else {
// 降序:拿着前面的元素值和后面的元素值进行比较,发现大的往前放
if (arr[i] < arr[j]) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}//内循环
}//外循环
}//方法3、二分法查找:
① 思路
② 具体查找过程
③ 代码实现
* 二分查找法
*
* @param arr
* @param key
* @return 要查找元素在数组中的索引,若返回值为-1说明没有要查找的元素,
*/
public static int binarySearch(int[] arr, int key) {
// 在不断缩小范围的过程中,可以
// 返回-1则说明找不到这个数
// 定义起始、终点、中间索引,目标key值索引
int start = 0;
int end = arr.length - 1;
// 在数组中找要找的数,因为不一定会一下子找到,所以这应该是一个重复寻找的过程,即会用到循环
while (start <= end) {// 看出start不断增大,end不断缩小;如果当start和end相等时都还找不到,start会继续增加,end继续变小,此时这已经不是一个正常的数组,结束循环
int middle = (start + end) / 2;
int value = arr[middle];
// 让中间索引对应的值value与要查找的值key进行比较
if (key == value) {
// 如果相等,即找到,则返回中间索引,并跳出循环
return middle;
} else if (key > value) { // key > value
if (arr[0] < arr[1]) { // 升序
start = middle + 1;
} else { // 降序
end = middle - 1;
}
} else { // key < value
if (arr[0] < arr[1]) { // 升序:end = middle - 1
end = middle - 1;
} else {// 降序:start = middle + 1
start = middle + 1;
}
}
} // while括号
return -1;
}