哈夫曼压缩
本博客已弃用,当时存在一些小细节错误后期也不再修改了
欢迎来我的新博客
前言:时隔大半年第二次写文件压缩,虽然并不是较难的项目,发现第二次写其实也并没有想象中在两个小时内写完,于是决定写这篇博客记录下来,分享给各位同学,提供一些学习过程的便利。
我会尽量写详细,讲清楚,适合有一定数据结构基础的同学。若有不足,欢迎指正。
正文:
知识要求:熟悉并掌握堆、熟悉并理解贪心算法、熟悉并掌握哈夫曼树、
哈夫曼编码
0.堆
相信学过或者对数据结构有基本了解的同学们一定都对堆不陌生。在此再给不太熟悉的同学回顾一下。
堆(heap)是一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
-
1.堆中某个节点的值总是不大于或不小于其父节点的值;
-
2.堆总是一棵完全二叉树。
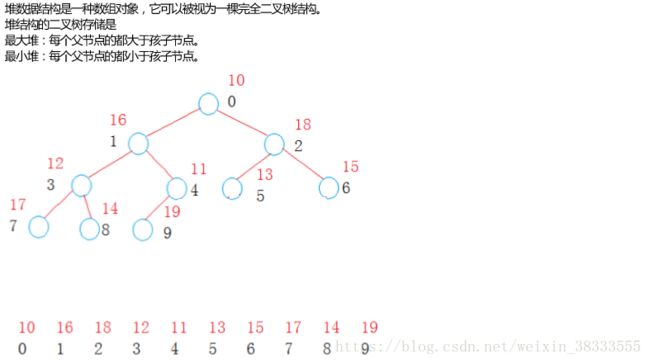
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆的严格定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆。
(ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)
若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非根结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
简单来说就是下面这样:
关于堆的具体实现,在此不进行详述过程,有许多讲解堆的博客,想了解的同学自行查阅。堆是后面的基础,有兴趣看下去的同学务必先弄清楚堆的实现。因为要做这个项目,必须要能自己去实现堆,虽然C++标准库里有堆可以用,但是如果你自己不能很好的理解堆的原理,那会导致出了bug你基本是不会调的,框架你基本是不会搭的,所以先把堆好好弄明白。(还是建议自己造个小轮子来用,因为标准库里的堆个人感觉不太好用 = =)
在此贴出堆的代码实现(仅包含我们需要用到的相关部分,后面解释为什么要用小堆):
#include
#include
#include
#pragma once
using namespace std;
template
struct Greater
{
bool operator () (const T& l,const T& r)
{
return l > r;
}
};
template
struct Less
{
bool operator () (const T& l,const T& r)
{
return l < r;
}
};
template>
class heap
{
public:
heap()
{
Size = 0;
}
heap(T* a,size_t n)
{
Size = n;
for(int i=0;i < n;i++)
{
v.push_back(a[i]);
}
//建堆
for(int i = (v.size()-2)/2;i >=0 ;i--)
{
Adjustdown(i);
}
}
void Adjustdown(size_t root)
{
Com com;
int parent = root;
int child = 2*parent+1;
while(child < v.size())
{
if(size_t(child+1) < v.size() && com(v[child+1],v[child]))
++child;
if(com(v[child],v[parent]))
{
swap(v[parent],v[child]);
parent = child;
child = 2*parent+1;
}
else
break;
}
}
T front()
{
assert(Size != 0);
return v[0];
}
void Adjustup(int child)
{
Com com;
int parent = (child-1)/2;
while (child > 0)
{
if(com(v[child],v[parent]))
{
swap(v[child],v[parent]);
child = parent;
parent = (child-1)/2;
}
else
break;
}
}
void push(T a)
{
Size++;
v.push_back(a);
Adjustup(v.size()-1);
}
void pop()
{
Size--;
swap(v[0],v[v.size()-1]);
v.pop_back();
Adjustdown(0);
}
size_t size()
{
return Size;
}
protected:
vector v;
size_t Size;
};
void testHeap()
{
int a[] = {9,3,1,7,4,2,6,8,5};
heap> h(a,9);
h.push(1);
cout<
1.贪心算法
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择(当前!这两个字很重要)。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解,也就是说我们希望通过局部最优达到优化整体的效果。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性(这个也很重要,看到后面就会知道了),即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
过程
-
1.建立数学模型来描述问题;
-
2.把求解的问题分成若干个子问题;
-
3.对每一子问题求解,得到子问题的局部最优解;
-
4.把子问题的解局部最优解合成原来解问题的一个解。
现在看不懂没关系,后面看到具体问题你就明白了。(其实就是一种优化思想,理解思想是本质,有很多问题其实都用到了贪心算法,说不定你以前隐约感觉到了这种方法,同学们可以自己去网上看看有哪些经典问题)
2.哈夫曼树
给定n个权值作为n个叶子节点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
哈夫曼树就是如上描述的这样一种二叉树,下面看看这个例子你就会明白哈夫曼树和贪心算法了。
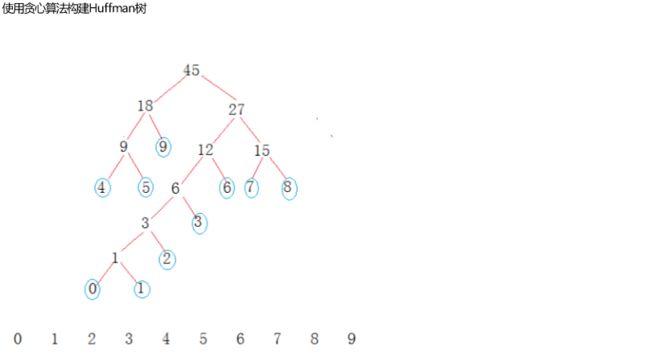
定义权值数组:int W[ ] = {0,1,2,3,4,5,6,7,8,9}
用权值数组构建出如下哈夫曼树
我们可以直接观察到的是:所有的权值,都在是叶子节点,并且很明显权值越大,离根节点越近,每个非叶子节点都是其左右节点的权值之和。
在哈夫曼树的定义中所指的“路径”二字,指的就是从根节点到该节点的距离。结合上图来看:比如从根节点要走到叶子节点4,那么路径就是:左->左->左;从根节点到叶子节点0,路径就是右->左->左->左->左->左。这些就是路径,然后显然从根走到叶子节点4需要走3次,走到叶子节点0要走6次,这里的“3次”、“6次”就是距离。你现在看看,是不是理解了哈夫曼树中带权路径最短是什么概念了。
接下来我们看如何构造一颗哈夫曼树。
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(第一步中这n棵树每棵仅有一个结点,该处要想明白不能单独当成n个节点,因为哈夫曼树建立中除了第一步,后面是需要把各个小树和节点相连的);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树(即(2)中得到的这棵)加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
你看,在重复(2)(3)步的时候,是不是就是在不断的从当前的子问题中找出局部最优。对应到上面的例子:
第一次选出0 、1 得到1,再把0,1从森林中删除,然后把新得到1(注意!这个1和第一次选出来的1不是一个东西了)放入森林,然后选出1、2得到3,再把1,2从森林中删除......如此循环,循环的终止条件:森林中只剩下一棵树(实际上这棵树是你通过上一次选出的两棵树所得到的新树)。这样最后剩下的这棵树就是我们要构造的哈夫曼树。在这个过程中我们在一开始把权值数组放入了小堆(也就是上面的森林)里,这样每次才能通过Top()Pop()Top()每次取得森林里权值最小的两棵树,并通过Push()放入每次得到的新树,然后进行循环操作。
你看,这样是不是就明白了堆、贪心算法、哈夫曼树各自是怎么回事并起了什么作用了。
值得提醒的是,我们应当在权值数组里放入的是指向节点的指针,不然一时马虎写成了传值,你会发现你的哈夫曼树就是连不起来你想要连起来的内部包含有权值的节点。
下面贴上哈夫曼树的相关代码以及每一步的注释(部分内容与后面的文件压缩有关,直接看可能会有看不懂的地方,可以看完了文件压缩的思路再回过头来看)
#include "heap.h"
#pragma once
using namespace std;
template
struct Node //Node为包含权值的节点。实际上根据后面文件压缩的需要_w中放的并不是权值,而是一个存有权值信息和其它信息的节点
{
W* _w;
Node* _left;
Node* _right;
Node(W* w, Node* left ,Node* right )
:_w(w),
_left(left),
_right(right)
{}
};
template
struct Com //根据后面文件压缩需要写的仿函数,也可以不放在哈夫曼树代码里,可以在使用哈夫曼树时定义
{
bool operator() (Node* l,Node* r)
{
return (l->_w)->_counts < (r->_w)->_counts;
}
};
template //模板参数I 为为后面文件压缩添加的一个非法值模板
class HuffmanTree
{
typedef Node Node;
public:
HuffmanTree(W* w,size_t n,I invalid)
{
//建小堆
heap minHeap;
for(int i = 0;i_w->_counts+right->_w->_counts ); //新树的根节点
Node* parent = new Node(_new,left,right);//该节点一定不是叶子节点,ch随意赋值,我们统一赋值为字符0
minHeap.push(parent); //把新树放入森林中
if(minHeap.size() == 1) //循环结束的条件
{
_root = parent; //得到所求的哈夫曼树
break;
}
}
}
Node* GetRoot()
{
return _root;
}
~HuffmanTree() //前序析构哈夫曼树
{
if(_root == NULL)
return;
Destroy(_root);
_root = NULL;
}
void Destroy(Node* root)
{
if(root == NULL)
return;
Node* left = root->_left;
Node* right = root->_right;
delete root;
root = NULL;
Destroy(left);
Destroy(right);
}
private:
Node* _root;
};
int deleted = 0;
//void TestHuffmanTree()
//{
//
// int a[] = {1,2,3,4,5,6,7,8,9};
// HuffmanTree,int> t(a,9,0);
// system("pause");
//} 3.哈夫曼编码
顺便介绍一下哈夫曼(David Huffman),对于学过数据结构的人来说,Huffman这个名字应该不会陌生。Huffman教授1999年10月7日逝世。在他的一生中,他对于有限状态自动机,开关电路,异步过程和信号设计有杰出的贡献。他发明的Huffman编码能够使我们通常的数据传输数量在一般情况下减少到最小,在是我们只是通过数据结构中的Huffman编码才了解这位杰出的科学家的。
这个人下面说一段哈夫曼编码创造的小历史,感兴趣的同学可以看一看,不感兴趣的跳过下一段。
1951年,哈夫曼和他在MIT信息论的同学需要选择是完成学期报告还是期末考试。导师Robert M. Fano给他们的学期报告的题目是,寻找最有效的二进制编码。由于无法证明哪个已有编码是最有效的,哈夫曼放弃对已有编码的研究,转向新的探索,最终发现了基于有序频率二叉树编码的想法,并很快证明了这个方法是最有效的。由于这个算法,学生终于青出于蓝,超过了他那曾经和信息论创立者香农共同研究过类似编码的导师。哈夫曼使用自底向上的方法构建二叉树,避免了次优算法Shannon-Fano编码的最大弊端──自顶向下构。
我们前面已经介绍过贪心算法与哈夫曼树,下面我们来举个例子来了解哈夫曼编码是怎么回事,并且,它又是怎么能达到文件压缩的效果的。
给定一个文本文件,内容为:aaaaabbbbcccdd
统计得每个字符出现的频率分别为:
a:5,b:4,c:3,d:2
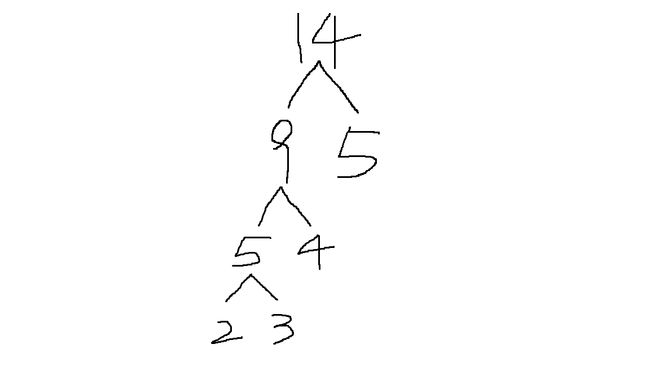
此时,把每个字符出现的频率当作权值,这样我们就能构建出一棵哈夫曼树如下(触控面板画图凑合着看=_=):
于是,我们定义向右走为1,向左走0,那么是不是到叶子节点2、3、4、5的分别为0000、0001、01、1
这就是哈夫曼编码:
a:1,b:01,c:0001,d:0000
是不是有个明显的特征就是出现频率越大的编码越短,也就是离根节点越近。并且值得注意的是:哈夫曼编码是前缀编码,即任一个字符的编码都不是另一个字符的编码的前缀,否则,编码就不能进行翻译(这一点是对应了前面贪心算法中的无后效性)。这样我们能通过原文件得到这样的一个以二进制方式写的huffman压缩文件:11111010 10101000 100010001 00000000(注意我们先不考虑计算机中一个字节八个比特位,先纯粹分析,不过这个例子刚好也不用补到八位)。你看,原文件是15个字节,压缩后就只有4个字节了,你看,是不是理论是很好的能把一个文件进行无损压缩的。然后,我们通过已知的哈夫曼编码又可以得到原文件(逆过程请同学自己分析,是怎么通过哈夫曼编码得到正确的原文件的)。(离哈夫曼编码被提出以来这么多年,毋庸置疑的是,它一直是无损压缩里最好的方法)
现在所有准备工作就都做完了,下面我会贴出压缩和解压的代码,其中我写有详细的注释和思路:
#pragma once
#include
#include "Huffman.h"
#include
//压缩:
//1.统计所有字符出现的次数,存入charInfo[256]
//2.用charInfo中权值不为0的字符构建哈夫曼树
//3.递归得到每个字符对应的哈夫曼编码
//4.把每个字符及其出现的频率按tmp结构体按二进制写入.huffman文件中(这样单独解压时就能再次生成哈夫曼编码了),然后一行二进制写入一个有效结构体,结尾写入一个标识结构体。
//再次打开原文件,把源文件按照哈夫曼编码按位写入.huffman(注意最后一个写入的字符可能不足八位,但解压时不能多读补位,下面会有解决方法)
struct charInfo
{
char _ch;
size_t _counts;
string _code;
charInfo(char ch,size_t counts,string code = "")
:_ch(ch)
,_counts(counts)
,_code(code)
{}
charInfo()
:_ch('0')
,_counts(0)
,_code("")
{}
};
class Compress
{
public:
Compress(char* filename)
{
cout<<"准备进行压缩"<,int> t(_charInfo,256,0);
//处理特殊情况,此时不用生成哈夫曼编码,直接写入一个结构体,那么就不在压缩文件中写任何其它信息了。直接在后面解压的部分对单个字符也特殊处理
if(t.GetRoot()->_left == NULL && t.GetRoot()->_right == NULL)
{
string huffman_file = _filename+".huffman";
const char* _huffman_file = huffman_file.data();
FILE* in_file = fopen(_huffman_file,"wb");
fwrite(t.GetRoot()->_w,sizeof(charInfo),1,in_file);
charInfo flag;
flag._counts = 0;
fwrite(&flag,sizeof(flag),1,in_file);
fclose(in_file);
return;
}
//生成哈夫曼编码
Generate_Huffman_Code(t);
//生成tmp只储存charInfo中权值不为0的字符与其出现频率,方便将huffman树中的字符与对应的频率参数写入文件开头,避免写入哈夫曼编码
charInfo tmp_charInfo[256];
for(size_t i = 0;i<256;i++)
{
if(_charInfo[i]._counts != 0)
{
tmp_charInfo[i]._ch = _charInfo[i]._ch;
tmp_charInfo[i]._counts = _charInfo[i]._counts;
}
}
//生成.huffman文件
string huffman_file = _filename+".huffman";
const char* _huffman_file = huffman_file.data();
FILE* in_file = fopen(_huffman_file,"wb");
long long byte_num_compressed = 0;
//有效的charInfo以二进制写入.huffman文件,并且在写完后写入一个权值为0设定为无效的charInfo作为结束标记
for(size_t i = 0;i<256;i++)
{
if(tmp_charInfo[i]._counts!=0)
{
fwrite(&tmp_charInfo[i],sizeof(charInfo),1,in_file);
byte_num_compressed++;
}
}
charInfo flag;
flag._counts = 0;
fwrite(&flag,sizeof(flag),1,in_file);
//再次打开原文件,将该文件中的内容以huffman_code按按位写入字符,然后二进制写入.huffman文件中
rewind(file); //把文件指针移到文件开头
char _ch = 0;
fread(&_ch,1,1,file);
char c = '0';
int pos = 0;
while(!feof(file) )
{
string code = _charInfo[unsigned char(_ch)]._code; //这一部分,还有后面解压部分的逻辑,同学们自己去想清楚
size_t i = 0;
while(i < code.size())
{
if( code[i] == '1')
c |= 1<,int>& t)
{
Node* _root= t.GetRoot();
string code("");
_Generate_Huffman_Code(_root,code);
}
void _Generate_Huffman_Code(Node* root,string code)
{
if(root->_left == NULL && root->_right == NULL)
{
(root->_w)->_code = code;
return;
}
_Generate_Huffman_Code(root->_left,code+"0");
_Generate_Huffman_Code(root->_right,code+"1");
}
};
//解压
//1.读.huffman文件 二进制读取文件前面的参数信息 写入_charInfo中 直到读到标记的停止的结构体,若是特殊情况按特殊情况处理
//2.生成哈夫曼树,生成哈夫曼编码
//3.用哈夫曼编码去翻译.huffman
class Uncompress
{
public:
Uncompress(const char* filename)
{
cout<<"开始解压"<_counts == 0) //说明有效结构体都已写入_charInfo,开始做后续工作
{
break;
}
else //该结构体为有效结构体
{
num++;
_charInfo[unsigned char(tmp_charInfo->_ch)]._ch = tmp_charInfo->_ch;
_charInfo[unsigned char(tmp_charInfo->_ch)]._counts = tmp_charInfo->_counts;
}
}
if(num == 1) //表明是特殊情况,直接解压
{
cout<<"解压中"<,int> t(_charInfo,256,0);
//生成哈夫曼编码
Generate_Huffman_Code(t);
//全部工作已经就绪,进行解压
cout<<"解压中"<_w->_counts; HuffmanTree,int>::Node* root = t.GetRoot();
HuffmanTree,int>::Node* cur = root;
while(1)
{
if(cur->_left == NULL && cur->_right == NULL) //左右都为空则到了叶子节点,写入
{
fwrite(&cur->_w->_ch,1,1,in_file);
--put_num;
cur = root;
}
if(((1<_right;
else
cur = cur->_left;
pos++;
if(pos == 8) //读完一个字符每一位读下一位
{
fread(&ch,1,1,file);
pos = 0;
}
if(put_num == 0)
{
cout<<"完成解压"<,int>& t)
{
Node* _root= t.GetRoot();
string code("");
_Generate_Huffman_Code(_root,code);
}
void _Generate_Huffman_Code(Node* root,string code)
{
if(root->_left == NULL && root->_right == NULL)
{
(root->_w)->_code = code;
return;
}
_Generate_Huffman_Code(root->_left,code+"0");
_Generate_Huffman_Code(root->_right,code+"1");
}
}; 我写的这个哈夫曼压缩叫做静态哈夫曼压缩,因为有人提出了更高效的动态哈夫曼编码,具体各位可以自行寻找相关博客(我没有找到写得比较好的讲动态哈夫曼的博客),个人感觉动态哈夫曼编码确实比静态哈夫曼编码复杂很多= =。
哈夫曼压缩到这儿就写完了,善于思考的同学可以意识到哈夫曼压缩也是有可以优化的地方的,比如连续的几个比特位上的1或者0或者其它排列,似乎又可以用某些指定的更短的编码代替,但是又要考虑编码的冲突问题,emmmmm......
其实还有不少问题可以去思考一下:比如,我们压缩后的文件我们再压缩一次会有什么效果?那么能不能无限压缩下去?压缩文件夹又是怎么进行的?
压缩技术在计算机行业中发展这么多年因为其重要性,已经成了水很深的东西,目前有许多种压缩算法。我们日常用过的.zip、.rar这些格式,都是老牌并且很厉害的压缩技术。人们似乎在这些事情上很喜欢追求极限,喜欢用最少的空间来传递最多的信号量,各位详见世界级别的压缩比赛。
就写到这儿了,前前后后各种事把这篇博客写了半个月才写完,点进来的同学就点个关注呗,如果有不明白的或者有发现写得不好的地方欢迎在评论指出。最后是代码的github链接:点我