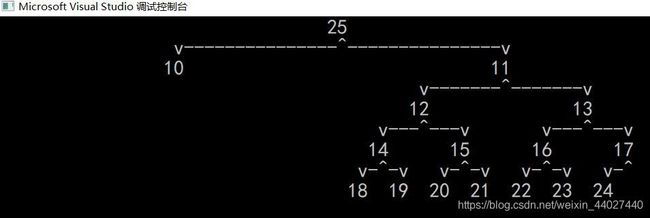
二叉树图形直观显示的完全实现
↵
经过进一步完善,二叉树的图形直观显示终于完成了。看效果图:
下面是原代码:
1、main()
//*****************************************************************************************
#include
#include
#include "BiTNode.h"
#include "BinaryTree.h"
#include "Queue.h"
#include "PrintLine.h"
using namespace std;
//*****************************************************************************************
//用数组创建二叉树
void CreateTree(int *arr,int left,int right, BiTNode *p);
int Main() {
根据数组随意创建一个二叉树
BiTNode *p=new BiTNode;
const int size = 16 ;
int a[size];
for (int i = 0;i < size;i++)
a[i] = i+10;
p->data =a[size-1];
CreateTree(a, 0, size - 2, p);
//通过复制的方式创建新的二叉树
BinaryTree intTree;
intTree.CreateTreeBy(p);
//使用二叉树的成员函数释放原来的只有Data,Lchild,Rchild简单信息的二叉树的内存空间
intTree.DeleteTree(p);
int parent, left, right;
parent = 10;
left = 99;
right = 98;
intTree.InsertTwoBiTNode(parent, left,right);
parent = 99;
right -= 1;
intTree.InsertBiTNode(parent, right,false);
//插入新节点之后必须重新生成二叉树。
intTree.ReCreateTree();
//图形直观显示二叉树
intTree.DisplayBinaryTree();
return 0;
}
void CreateTree(int *arr, int left, int right,BiTNode *p) {
if (p) {
if (left == right) {
BiTNode *newnode=new BiTNode;
newnode->data = arr[left];
if (!p->Lchild)
p->Lchild = newnode;
else if (!p->Rchild)
p->Rchild = newnode;
}
if (left < right) {
int mid = (left + right) / 2;
if(p->Lchild)
CreateTree(arr, left, mid, p->Lchild);
else
CreateTree(arr, left, mid, p);
if(p->Rchild)
CreateTree(arr, mid + 1, right, p->Rchild);
else
CreateTree(arr, mid + 1, right, p);
}
}
}
2、Queue.h
#pragma once
using namespace std;
//队列内元素最大个数:
static const int MAXSIZE=100;
/*模板队列类
*/
template
class Queue {
private:
//队首,指向最先出队列的元素位置。
int front;
//队尾,指向下一次插入的新元素位置。
int rear;
//已经插入队列的元素个数。
int count;
//队列内保存元素的数组。
T qList[MAXSIZE];
public:
//构造函数
Queue();
//插入元素的函数
bool QInsert(T& item);
//弹出元素的函数
T QDelete(void);
//清空队列
void QClear(void);
//返回正在排队的元素个数。
int QGetCount(void);
//队列状态函数:是否为空。
bool QEmpty();
//队列状态函数:是否已满。
bool QFull();
//析构函数
~Queue();
};
template
Queue::Queue() :front(0),rear(0),count(0){
}
template
bool Queue::QInsert(T& item){
if (QFull()) {
cout << "队列已满!插入失败!" << endl;
return false;
}
else {
count++;
qList[rear] = item;
rear = (rear + 1) % MAXSIZE;
return true;
}
}
template
T Queue::QDelete(void){
if (QEmpty()) {
cout << "队列是空的!非正常退出!" << endl;
exit(1);
}
else {
T temp = qList[front];
count--;
front = (front + 1) % MAXSIZE;
return temp;
}
}
template
void Queue::QClear(void){
front = rear =count= 0;
}
template
int Queue::QGetCount(void) {
return count;
}
template
bool Queue::QEmpty(){
return count == 0;
}
template
bool Queue::QFull(){
return count == MAXSIZE;
}
template
Queue::~Queue() {
} 3、BiTNode.h
#pragma once
template
struct BiTNode {
BiTNode *Lchild=NULL, *Rchild=NULL,*parent=NULL;
T data;
int depth=0;
int order = 0;
};
4、PrintLine.h
#pragma once
#include
#include "BiTNode.h"
using namespace std;
//每个节点(根结点除外)对应要输出的连接符号的类型
enum LineType { LRline ,RLline, Lline, Rline };
//定义与输出连接符号相关的结构类,主要用于定义输出连接符号的方法。
template
struct PrintLine
{
static const int DeltaWidth=4;
static LineType GetLineType(BiTNode *p);
static void Print(int width, int deltawidth,int distance, LineType line);
};
//获取每个节点(根结点不需要)需要添加的连续符号的类型。
//此类型在PintLine::LineType中定义的。
template
LineType PrintLine::GetLineType(BiTNode *p) {
if (p->order % 2) {//order为偶数,说明为右节点。
if (p->parent->Lchild) {
return LineType::RLline;//当前为右节点,并且存在左节点。
}
else {
return LineType::Rline;//当前为右节点,并且没有左节点。
}
}
else {//order为奇数,说明为左节点。
if (p->parent->Rchild) {
return LineType::LRline;//当前为左节点,并且存在右节点。
}
else {
return LineType::Lline;//当前为左节点,并且没有右节点。
}
}
}
//输出与某一层节点对应的连接符号。
//输出如:v-----^-----v的连接符号,用于父节点与左右子节点之间的连接,直观显示它们的关系。
template
void PrintLine::Print(int width, int deltawidth, int distance, LineType line) {
char childC = 118;//左或右节点对应的符号:v
char parentC = 94;//父节点对应的符号:^
char lineC = '-';//节点符号中间的连接符号
char c;//输出时未用完的空间所使用的填充的符号
switch (line)
{
//左右子节点都有时的左子节点
//如果是左右节点中的左节点时,把左右节点对应的连接符号全部输出
//如果是左右节点中的右节点时就什么也不做
case LRline:
cout.width(width);
cout << childC;
c = cout.fill(lineC);
cout.width(distance + deltawidth / 2);
cout << parentC;
cout.width(distance + deltawidth - deltawidth / 2);
cout << childC;
cout.fill(c);
break;
//只有左子节点的情况
case Lline:
cout.width(width);
cout << childC;
c=cout.fill(lineC);
cout.width(distance + deltawidth / 2);
cout << parentC;
cout.fill(c);
break;
//左右子节点都有时的右子节点
case RLline:
break;
//只有右子节点的情况
case Rline:
cout.width(width-deltawidth-distance+ deltawidth / 2);
cout << parentC;
cout.width(distance+deltawidth- deltawidth / 2);
c = cout.fill(lineC);
cout << childC;
cout.fill(c);
break;
default:
break;
}
} 5、BinaryTree.h
#pragma once
#include
#include
#include "BiTNode.h"
#include "../Queue/Queue.h"
#include "PrintLine.h"
using namespace std;
template
class BinaryTree {
private:
BiTNode *root;
void PreOrder(BiTNode *root);
void InOrder(BiTNode *root);
void PostOrder(BiTNode *root);
int CountDepth(BiTNode *root);
int CountLeaf(BiTNode *root);
void AddInfoToBiTNode(BiTNode *p);
void CreateTree(BiTNode *root);
void ManualCreate(BiTNode *p);
public:
BinaryTree();
BinaryTree(BiTNode *root);
~BinaryTree();
bool InsertBiTNode(T& parentitem, T& childitem, bool IsLeft = true);
bool InsertTwoBiTNode(T& parentitem, T& leftchilditem, T& rightchilditem);
void ReCreateTree(void);
void CreateTreeBy(BiTNode *p);
void DeleteTree(BiTNode *root);
int GetDepth();
int GetLeafNum(void);
void PreOrderListTree(void);
void LayerOrderListTree(void);
void InOrderListTree(void);
void PostOrderListTree(void);
void ManualCreateTree(void);
void DisplayBinaryTree(void);
BiTNode *GetRootBiTNode(void)const;
BiTNode *GetBiTNode(T& item);
BiTNode *GetBiTNodeByParent(T& parentitem,bool isLeft=true);
};
template
void BinaryTree::AddInfoToBiTNode(BiTNode *p) {
//复制p为根结点的树,并添加BiTNode相关变量信息。
Queue *> qbit;
BiTNode *bitNode,*childNode;
if (p) {
//根结点复制
root = new BiTNode;
root->data = p->data;
root->depth = 1;
//ordero为节点序号。节点序号编排原则:从0开始;空节点也要占据相应位置。非实际节点序号。
root->order = 0;
root->Lchild = p->Lchild;
root->Rchild = p->Rchild;
qbit.QInsert(root);
//其它节点的复制循环,利用队列先进先出特点,按层序复制所有节点。
while (!qbit.QEmpty()) {
bitNode = qbit.QDelete();
//根据父结点,创建左子节点并添加相关信息。
if (bitNode->Lchild) {
childNode = new BiTNode;
childNode->data = bitNode->Lchild->data;
childNode->depth = bitNode->depth + 1;
childNode->parent = bitNode;
//根据父节点的序号确定上一层元素的个数,从而可以确定当前节点在当前层的序号。
//序号计算要包括父结点中不存在的左或右子节点的数量。序号不是指实际存在的同层节点的序号。
childNode->order = childNode->parent->order * 2 ;
childNode->Lchild = bitNode->Lchild->Lchild;
childNode->Rchild = bitNode->Lchild->Rchild;
bitNode->Lchild = childNode;
qbit.QInsert(bitNode->Lchild);
}
//根据父结点,创建右子节点并添加相关信息。
if (bitNode->Rchild) {
childNode = new BiTNode;
childNode->data = bitNode->Rchild->data;
childNode->depth = bitNode->depth + 1;
childNode->parent = bitNode;
childNode->order = childNode->parent->order * 2 + 1;
childNode->Lchild = bitNode->Rchild->Lchild;
childNode->Rchild = bitNode->Rchild->Rchild;
bitNode->Rchild = childNode;
qbit.QInsert(bitNode->Rchild);
}
}
}
}
template
void BinaryTree::CreateTree(BiTNode *root) {
AddInfoToBiTNode(root);
}
template
void BinaryTree::ReCreateTree(void) {
BiTNode *temp=root;
root = NULL;
CreateTree(temp);
DeleteTree(temp);
}
template
BinaryTree::BinaryTree():root(NULL) {
}
template
BinaryTree::BinaryTree(BiTNode *root){
CreateTree(root);
}
template
void BinaryTree::CreateTreeBy(BiTNode *p) {
CreateTree(p);
}
template
BinaryTree::~BinaryTree() {
DeleteTree(root);
root = NULL;
}
//
template
void BinaryTree::DeleteTree(BiTNode *root) {
if (root != NULL) {
if (root->Lchild) {
DeleteTree(root->Lchild);
}
if (root->Rchild) {
DeleteTree(root->Rchild);
}
delete root;
}
}
//
//计算二叉树的深度
template
int BinaryTree::CountDepth(BiTNode *root) {
int leftdepth, rightdepth, maxdepth;
if (root == NULL)
return 0;
leftdepth = CountDepth(root->Lchild);
rightdepth = CountDepth(root->Rchild);
maxdepth = leftdepth < rightdepth ? rightdepth : leftdepth;
return maxdepth + 1;
}
template
int BinaryTree::GetDepth() {
return CountDepth(root);
}
//计算二叉树的叶子总数
template
int BinaryTree::CountLeaf(BiTNode *root) {
if (root == NULL)
return 0;
if ((root->Lchild == NULL) && (root->Rchild == NULL))
return 1;
return CountLeaf(root->Lchild) + CountLeaf(root->Rchild);
}
template
int BinaryTree::GetLeafNum(void) {
return CountLeaf(root);
}
//先序显示树
template
void BinaryTree::PreOrderListTree(void) {
PreOrder(this->root);
cout << endl;
}
template
void BinaryTree::PreOrder(BiTNode *root) {
if (root) {
cout << root->data << " ";
if (root->Lchild) {
PreOrder(root->Lchild);
}
if (root->Rchild) {
PreOrder(root->Rchild);
}
}
}
//中序遍历二叉树
template
void BinaryTree::InOrder(BiTNode *root) {
if (root) {
if (root->Lchild)
InOrder(root->Lchild);
cout << root->data<<" ";
if (root->Rchild)
InOrder(root->Rchild);
}
}
template
void BinaryTree::InOrderListTree(void) {
InOrder(root);
cout << endl;
}
//后序遍历二叉树
template
void BinaryTree::PostOrder(BiTNode *root) {
if (root) {
if (root->Lchild)
InOrder(root->Lchild);
if (root->Rchild)
InOrder(root->Rchild);
cout << root->data << " ";
}
}
template
void BinaryTree::PostOrderListTree(void) {
PostOrder(root);
cout << endl;
}
//按层遍历二叉树
template
void BinaryTree::LayerOrderListTree(void) {
Queue*> qbit;
BiTNode *p;
if (root) {
qbit.QInsert(root);
while (!qbit.QEmpty()) {
p = qbit.QDelete();
cout << p->data << " ";
if (p->Lchild) {
qbit.QInsert(p->Lchild);
}
if (p->Rchild) {
qbit.QInsert(p->Rchild);
}
}
cout << endl;
}
}
//获取节点
template
BiTNode *BinaryTree::GetRootBiTNode(void)const {
return root;
}
template
BiTNode *BinaryTree::GetBiTNode(T& item) {
Queue*> qbit;
BiTNode *p=NULL;
if (root) {
qbit.QInsert(root);
while (!qbit.QEmpty()) {
p = qbit.QDelete();
if (p->data == item)
break;
if (p->Lchild) {
qbit.QInsert(p->Lchild);
}
if (p->Rchild) {
qbit.QInsert(p->Rchild);
}
}
return p;
}
return NULL;
}
template
BiTNode *BinaryTree::GetBiTNodeByParent(T& parentitem, bool isLeft) {
Queue*> qbit;
BiTNode *p = NULL;
if (root) {
qbit.QInsert(root);
while (!qbit.QEmpty()) {
p = qbit.QDelete();
if (p->data == parentitem) {
return isLeft ? p->Lchild : p->Rchild;
}
if (p->Lchild) {
qbit.QInsert(p->Lchild);
}
if (p->Rchild) {
qbit.QInsert(p->Rchild);
}
}
return NULL;
}
else {
return NULL;
}
}
//插入节点
template
bool BinaryTree::InsertBiTNode(T& parentitem, T& childitem, bool IsLeft) {
BiTNode *tempBiTNode = GetBiTNode(parentitem);
if (tempBiTNode) {
if ((!tempBiTNode->Lchild) && (IsLeft)) {
tempBiTNode->Lchild = new BiTNode;
tempBiTNode->Lchild->data = childitem;
return true;
}
else if ((!tempBiTNode->Rchild) && (!IsLeft)) {
tempBiTNode->Rchild = new BiTNode;
tempBiTNode->Rchild->data = childitem;
return true;
}
return false;
}
else {
return false;
}
}
template
bool BinaryTree::InsertTwoBiTNode(T& parentitem, T& leftchilditem, T& rightchilditem) {
BiTNode *tempBiTNode = GetBiTNode(parentitem);
if (tempBiTNode) {
if ((!tempBiTNode->Lchild) && (!tempBiTNode->Rchild)) {
tempBiTNode->Lchild = new BiTNode;
tempBiTNode->Lchild->data = leftchilditem;
tempBiTNode->Rchild = new BiTNode;
tempBiTNode->Rchild->data = rightchilditem;
return true;
}
return false;
}
else {
return false;
}
}
//手动创建二叉树
template
void BinaryTree::ManualCreate(BiTNode *p) {
int val;
if (p) {
cout << "请输入 " << p->data << " 的左子节点的值:";
cin >> val;
if (val != -1) {
p->Lchild = new BiTNode;
p->Lchild->data = val;
}
cout << "请输入 " << p->data << " 的右子节点的值:";
cin >> val;
if (val != -1) {
p->Rchild = new BiTNode;
p->Rchild->data = val;
}
//
ManualCreate(p->Lchild);
ManualCreate(p->Rchild);
}
}
template
void BinaryTree::ManualCreateTree(void) {
int val;
BiTNode *r;
cout << "请输入二叉树根的值:";
cin >> val;
if (val != -1) {
if (root)
DeleteTree(root);
root = new BiTNode;
root->data = val;
ManualCreate(root);
CreateTree(root);
}
}
//图形显示二叉树
template
void BinaryTree::DisplayBinaryTree(void) {
//利用ostringstream流把节点输出的内容输出到ostringstream中,然后再输出到cout上。
ostringstream oss;
//利用队列作为读取二叉树节点的工具
Queue*> qbit;
//记录前后两个节点的指针
BiTNode *p, *pre;
//需要显示的节点值的宽度。
//偶数最佳,否则有可能数据精度受影响,造成输出不均等。
//根据显示调节宽度。不宜太大。定义在模板结构PrintLine里面。
int deltawidth = PrintLine::DeltaWidth;
//整个二叉树的深度(最大层数)
int treeDepth = GetDepth();
//根据二叉树最大一层可能存在的元素最多个数确定输出的最大宽度。此变量未使用,用于理解。
//int maxwidth = deltawidth * pow(2, treeDepth - 1);
//元素之间间距变量
//二叉树每层元素以一定宽度输出后,在上述最大宽度输出范围内,剩余的元素之间的空白宽度
//计算公式:(2^(最大层数-当前层数)-1)/2 ,其中层数从1开始。
//每层第一个节点之前,最后一个节点之后的缩进宽度为:1*distance。两个节点之间为2*distance宽度。
int distance;
//二叉树深度(层数)
int depth;
//同层元素的序号:从0开始,每层元素为:2^(层数-1)个。每层最大序号为:2^(层数-1)-1 个。
int order;
//每层可能存在的元素的最大个数。
int nodesNum;
//二叉树每层最后一个元素输出后,接着输出换行符后的标志设置
int flagEnter = 0;
//上一个元素的序号
int _preOrder;
//上一个元素指针(初始为根结点)
pre = root;
/*以下利用队列先进先出的特点,循环读取二叉树节点,
按层序由根结点到最大层从左到右依次读取元素,
并根据获取的元素相关信息格式化输出二叉树每层元素。
当遍历二叉树又不想用递归方法时,利用队列的先进先出的特点就能实现遍历了。
*/
if (root) {
qbit.QInsert(root);
while (!qbit.QEmpty()) {
//每个节点输出时的输出宽度的变量(用于计算节点输出宽度的过程中的累计)
int totalwidth = 0;
p = qbit.QDelete();
//当前节点的深度(层数)
depth = p->depth;
//当前节点的序号(即二叉树某层第几个节点)
order = p->order;
//每层元素总数(包括空节点)
nodesNum = pow(2, depth - 1);
if (pre->depth != p->depth) {
cout << oss.str();//输出同层所有节点
oss.str("");//输出后清空,然后开始新的一层节点的输出
oss << endl;
flagEnter = 1;
}
//单位间距变量(关键点!!!)
//根据二叉树的层数(深度)和自定义设置的元素输出的单位宽度,
//直接计算出元素之间的间距的单位量:元素之间的间距=2*distance.
//每层的间距不一样,最大一层间距为0.即distance为0.
distance = deltawidth * (pow(2, treeDepth - depth) - 1) / 2;
//根结点所在层,即第一层单独设置输出宽度。
//第一层:maxwidth=distance+节点(按一定单位的宽度输出)+distance.
if (depth == 1) {
totalwidth = distance + deltawidth;
oss.width(totalwidth);
}
else {
//以下为:非第一层节点输出的宽度的计算方法
//如果上一节点是上一层最后一个元素输出并输出了换行符,
//下一行开始(即当前节点)就要首先输出一个缩进宽度。即为distance的值。
if (flagEnter == 1) {
totalwidth += distance;
flagEnter = 0;
}
//存在每层第一个存在的元素的序号不是为0的情况,统一把它第一个元素的序号设置成-1,
//方便计算元素之间的间距(不一定是序号相连的两个元素)
if (pre->depth != depth) {
_preOrder = -1;
}
else {
//不是第一个的元素的序号仍然为原序号。
_preOrder = pre->order;
}
//每个元素的输出宽度的计算公式(元素本身的宽度+元素之间间距)--(实际存在的元素之间不一定序号相连)。
//同层序号相连的两个元素之间的间距=2*distance.
totalwidth += (order - _preOrder)*(deltawidth + 2 * distance) - 2 * distance;
oss.width(totalwidth);
}
//输出元素(节点)的值
oss << p->data;
//每个元素输出后的间距输出。最深一层(最大层)的间距为0,不输出。
if ((depth != treeDepth) && (order < nodesNum - 1)) {
oss.width(2 * distance);
oss << " ";
}
//cout.fill(c);
//开始输出符号----------------------------
if (p->depth != pre->depth) {
cout << endl;
}
//开始输出节点对应的符号-------------------------------------------------------
if (p != root) {
//获取当前节点对应的要添加的符号类型。类型定义见:LineType
LineType Ltype = PrintLine::GetLineType(p);
//分情况输出符号
if (p->depth != pre->depth) {
//每层第一个节点或前面节点都是空节点之后的第一个节点
PrintLine::Print(totalwidth, deltawidth, distance, Ltype);
}
else {
if (PrintLine::GetLineType(pre) == LineType::Lline) {
//只有左节点,没有右节点
PrintLine::Print(totalwidth + distance - deltawidth / 2, deltawidth, distance, Ltype);
}
else {
//除以上两种情况以外的情况
PrintLine::Print(totalwidth + 2 * distance, deltawidth, distance, Ltype);
}
}
}
//结束输出符号--------------------------------------------------------------------
//把当前节点设置成下一个节点的前一个节点。
pre = p;
//按层序原则循环输出其它元素。搞定!!!
if (p->Lchild) {
qbit.QInsert(p->Lchild);
}
if (p->Rchild) {
qbit.QInsert(p->Rchild);
}
}
//最后一层节点的输出
cout << oss.str();
//清空流
oss.str("");
//输出最后一个换行符。
cout << endl;
}
}