1.绘制三维图形的基本函数
最基本的三维绘图函数为plot3;
plot3与plot用法十分相似,调用格式:
plot(x1,y1,z1,选项1,x2,y2,z2,选项2,...,xn,yn,zn,选项n)
当x,y,z是同维向量时,则x,y,z,对应元素构成一条三维曲线;
当x,y,z是同维矩阵时,则以x,y,z对应列元素绘制三维曲线,曲线条数等于矩阵列数。
例:
程序如下:
t=0:pi/50:2*pi;
x=8*cos(t);
y=4*sqrt(2)*sin(t);
z=-4*sqrt(2)*sin(t);
plot3(x,y,z,'p');
title('Line in 3-D Space');
text(0,0,0,'origin');
xlabel('x'),ylabel('y'),zlabel('z');
grid;
2.三维曲面
2.1平面网格坐标矩阵的生成
绘制z=f(x,y)所代表的三维曲面图,先要在xy平面选定一个矩形区域,假定矩形区域D=[a,b]*[c,d],然后将[a,b]在x方向分成m份,将[c,d]在y方向分成n份,由各划分点分别作平行于两坐标轴的直线,将区域D分成m*n个小矩形,生成代表每一个小矩形顶点坐标的平面网格坐标矩阵,最后利用有关函数绘图。
产生平面区域内的网格坐标矩阵有两种方法:
1.利用矩阵运算生成、
x=a:dx:b;
y=(c:dy:d)';
X=ones(size(y))*x;
Y=y*ones(size(x));
语句执行后,
矩阵X的每一行都是向量x,行数等于向量y的元素个数,
矩阵Y的每一列都是向量y,列数等于向量x的元素个数。
于是对于矩阵X,Y来说,它们位置(i,j)上的元素值(X(i,j),Y(i,j))就是所要形成的平面网格
在位置(i,j)上的X,Y坐标。可根据每一个网格点上的x,y坐标求这个点对应的z,则得到Z矩阵。
显然,X,Y,Z各列或各行所对应坐标,对应于一条空间曲线,空间曲线的集合将可组成空间曲面。
2.利用meshgrid函数生成。
调用格式:
x=a:dx:b;
y=c:dy:d;
[x,y]=meshgrid(x,y);
语句执行后得到与方法1相同的矩阵X,Y。
当向量x=y时,函数可写成meshgrid(x);
例:利用法网格坐标阵巧解不定方程:
已知6 两个函数: 例5.15:用三维曲面图表现函数z=sinycosx。 program1:用meshgrid+mesh x=0:0.1:2*pi; program2:用meshgrid+surf program3:用一般绘图函数plot3 例5.16:绘制两个直径相等的圆管的相交图形。 程序如下: 将上述例5.16中程序的%备注取消,即将第一图的y阵第二图的z阵转置,这样在底层面就不再是圆线了,效果如下: 例5.17 分析由函数z=x^2-2y^2构成的曲面形状及与平面z=a的交线。 a=?8 ans = 101 101 此外,还有两个和mesh函数相似的函数,即带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。其用法与mesh类似,不同的是meshc还在xy平面上绘制曲面在z轴方向的等高线,meshz还在xy平面上绘制曲面的底座。 例5.18 在xy平面内选择区域[-8,8]*[-8,8],绘制函数 程序如下: MATLAB提供了一些函数用于绘制标准三维曲面,这些函数可以产生相应的绘图数据,常用于三维图形的演示。例如: sphere函数和cylinder函数分别用于绘制三维球面和柱面。其调用格式为: MATLAB还有一个peaks函数,称为多峰函数,,常用于三维曲面的演示。该函数可以用来生成绘图数据矩阵,矩阵元素由函数: 在矩形区域[-3,3]*[-3,3]的等分网格点的函数值确定。例如: z=peaks(30); 将生成一个30*30矩阵z,即分别沿x和y方向将区间[-3,3]等分成29份,并计算这些网格点上的函数值。默认的等分数是48,即p=peaks将生成一个49*49矩阵p。也可以根据风格坐标矩阵x、y重新计算函数值矩阵。例如: [x,y]=meshgrid(-5:0.1:5); z=peaks(x,y); 生成的数值矩阵可以作为mesh、surf等函数参数而绘制出发多峰函数曲面图。另处,若在调用peaks函数时不带输出参数,则直接绘制出多峰函数曲面图。 例5.19 绘制标准三维曲面图形。 程序如下: 例:1.bar3(y) (1)当y为矩阵时,以元素下标为坐标,以元素值为高度,绘制条形图。 (2)当y为向量时,也是以下标为坐标,为值为高度。 2.bar3(x,y) (1)x为向量,y为向量 (1)x为向量,y为矩阵(x元素改变y矩阵的x坐标) 1.stem3(z) (1)z为矩阵,以下标为坐标,值为杆值 (2)z为向量,以下标为坐标,值为杆值 2.stem3(x,y,z) (1)x,y,z均为向量,以(x,y)为对应坐标z为值 x=7:29;
y=16:35;
[x,y]=meshgrid(x,y); %在[7,29]*[16,35]区域生成网格坐标
z=2*x+5*y;
k=find(z==126);%找出解的位置,即k为z中元素等于126的元素的位置
x(k)',y(k)'%输出对应位置的x,y即方程的解
输出:
ans =
8 13 18 23
ans =
22 20 18 16
%即方程有4组解:(8,22),(13,20),(18,18)(23,16).
输出:
>> k
k =
27
125
223
321
输出(关于find函数):
>> [a,b]=find(z==126)
a =
7
5
3
1
b =
2
7
12
17
>> x(7,2)
ans =
8
2.2 绘制三维曲面的函数
mesh(x,y,z,c)%用于绘制三维网格图,在不需要绘制特别精细三维曲面时使用。
surf(x,y,z,c)%用于绘制三维曲面,各线条之间的补面用颜色填充。
关于x,y,z,c:
one:通常x,y,z是同维矩阵,x,y是网格坐标矩阵,z是网格点的高度矩阵,c用于指定在不同高度下的颜色范围。
two:c省略时,MATLAB认为c=z,即颜色的高度正比于图形高度,以得到层次分明的三维图形。当x,y省略时,把z矩阵的列下标当做x轴坐标,把z矩阵的行下标当做y轴坐标,然后绘制三维曲面图。
three:当x,y是向量时,要求x的长度必须等于z矩阵的列数,y的长度等于z矩阵的行数,x,y向量元素的组合构成网格点的x,y坐标,z坐标则取自z矩阵,然后绘制三维曲面图。
x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
mesh(x,y,z);
xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');
title('mesh');
效果同:
y=0:0.1:2*pi;
z=sin(y')*cos(x);
mesh(x,y,z);
xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
surf(x,y,z);
xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');
title('meshgrid+surf');
x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
plot3(x,y,z);
xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');
title('meshgrid+plot3-1f');
grid;
%两个等直径圆管的交线
m=60;%m是圆圈的密集度,表示画60个圆圈
z=1.2*(0:m)/m;%1.2是圆柱高
r=ones(size(z));
theta=(0:m)/m*2*pi;
x1=r'*cos(theta);%每行都是一个cos(theta)
y1=r'*sin(theta);%每行都是一个sin(theta)
%y1=y1';
z1=z'*ones(1,m+1);%每行的z相同
surf(x1,y1,z1);%绘图,立起的圆柱
%axis equal,axis off
hold on
x=(-m:2:m)/m;
x2=x'*ones(1,m+1);%m+1个x列
y2=r'*cos(theta);%以y和z为底画圆
%y2=y2';
z2=r'*sin(theta);
surf(x2,y2,z2);
axis equal,axis off
title('两个等直径圆管的交线');
hold off
[x,y]=meshgrid(-10:0.2:10);
z1=(x.^2-2*y.^2)+eps;%第一个曲面
a=input('a=?');
z2=a*ones(size(x));%第二个曲面(本质是一个数乘)
subplot(1,2,1);
mesh(x,y,z1);hold on;mesh(x,y,z2);%分别画出两个曲面
v=[-10,10,-10,10,-100,100];axis(v);grid;%第一个子图的坐标设置
hold off;
r0=(abs(z1-z2)<=1);%求两曲面z坐标差小于1的点,r0只有0、1值
xx=r0.*x;yy=r0.*y;zz=r0.*z2;%求这些点上的x,y,z坐标,即交线坐标
subplot(1,2,2);
plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'*');%在第2子图画出交线
axis(v);grid;%第2子图的坐标设置
size(x)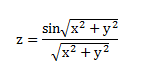 的4种三维曲面图。
的4种三维曲面图。[x,y]=meshgrid(-8:0.5:8);
z=sin(sqrt(x.^2)+y.^2)./sqrt(x.^2+y.^2+eps);
subplot(2,2,1);
meshc(x,y,z);
title('meshz(x,y,z)')
subplot(2,2,2);
meshz(x,y,z);
title('meshz(x,y,z)')
subplot(2,2,3);
surfc(x,y,z)
title('surfc(x,y,z)')
subplot(2,2,4);
surfl(x,y,z)
title('surf1(x,y,z)')
3.标准三维曲面
sphere函数的调用格式为:
[x,y,z]=sphere(n)
该函数将产生(n+1)*(n+1)矩阵x,y,z,采用这3个矩阵可以绘制出圆心位于原点、半径为1的单位球体。
若在调用该函数时不带输出参数,则直接绘制所需球面。n决定了球面的圆滑程度,其默认值为20.若n值取得较小,则将绘制出多面体表面图。
cylinder函数调用格式为:
[x,y,z]=cylinder(R,n)
其中,R是一个向量,存放柱面各个等间隔高度上的半径,n表示在圆柱圆周上有n个间隔点,默认有20个间隔点。例如,cylinder(3)生成一个圆柱,cylinder([10,1])生成一个圆锥,
而
t=0:pi/100:4*pi;
R=sin(t);
cylinder(R,30)
生成一个正弦柱面。
另外,生成矩阵的大小与R向量的长度及n有关。其余与sphere函数相同。
t=0:pi/20:2*pi;
[x,y,z]=cylinder(2+sin(t),30);
subplot(1,3,1);
surf(x,y,z);
subplot(1,3,2);
[x,y,z]=sphere;
surf(x,y,z);
subplot(1,3,3);
[x,y,z]=peaks(30);
meshz(x,y,z);
4.其它三维图形
4.1 三维条形图
bar3函数绘制三维条形图,调用格式为:
bar3(y)
bar3(x,y)
在第一种格式中,y的每个元素对应一个条形。
第二种格式在x指定 的位置上绘制y中元素的条形图,X为向量,当y为向量时,x元素个数与y列数相同,当y为矩阵时,x元素与y的行数相同。
>> y=magic(5)
y =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> y(5,:)=[]%删除第五行
y =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
>> bar3(y)
>> y=[1 3 5 7 2]
y =
1 3 5 7 2
>> bar3(y)
>>
>> y
y =
1 3 5 7 9 11
>> x
x =
1 3 5 4 8 11
>> bar3(x,y)
>>
y =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
>> x=[1 3 5 9]
x =
1 3 5 9
>> bar3(x,y)
4.2 三维杆图stem3(z)
stem3(x,y,z)
第一种格式将 数据序列z 表示为xy平面向上延伸的杆图,x和y自动生成。
第二种格式在x和y指定位置上绘制 数据序列z的杆图,x,y,z的维数必须相同。
z =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
>> stem3(z)
z=y(1,:)
z =
17 24 1 8 15
>> stem3(z)
>> stem(z)
x =
1 2 5 9 6
>> y=x
y =
1 2 5 9 6
>> z=x
z =
1 2 5 9 6
>> stem3(x,y,z)
>>
4.3 三维饼图
pie3(x)
其中x为向量,用x中的数据绘制一个三维饼图。
pie3([2347 1827 2043 3025])
pie([2347 1827 2043 3025])
4.4 填充多边形
fill3(x,y,z,c)
使用x,y,z作为多边形的顶点,用c指定了填充的颜色。
fill(x,y,c)
以(x,y)为点,c为颜色图,连点并填充点间面。
x =
1 5 6 8
>> y
y =
2 6 4 6
>> z=[1 2 3 4 5 ]
z =
1 2 3 4 5
>> fill(x,y,z)
fill3(rand(3,5),rand(3,5),rand(3,5),'y')
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第1张图片](http://img.e-com-net.com/image/info8/86ebecf36aec4f04aaaf65cf3c7cd957.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第2张图片](http://img.e-com-net.com/image/info8/3c9fa77b727b4d2db5932970778b7b44.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第3张图片](http://img.e-com-net.com/image/info8/4be55444b6f048d3906062fc3e16620d.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第4张图片](http://img.e-com-net.com/image/info8/ac0f2b1905174513b369f2886f7428e1.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第5张图片](http://img.e-com-net.com/image/info8/b6889483bb6a4b99a508e3162016f571.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第6张图片](http://img.e-com-net.com/image/info8/ba1e33bcec884ec0a30439b9fb48b2d0.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第7张图片](http://img.e-com-net.com/image/info8/33290a5c00254c6db13baa877e30aa96.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第8张图片](http://img.e-com-net.com/image/info8/57176677e4dc41f982d1866111ca0d66.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第9张图片](http://img.e-com-net.com/image/info8/53cbc253c231408c927d6aa8d73982fa.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第10张图片](http://img.e-com-net.com/image/info8/d939a59f159d44ec88db80fb9a9151f9.jpg)
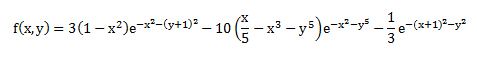
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第11张图片](http://img.e-com-net.com/image/info8/ef80ad22bc974ad58ba9c6f6f557c223.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第12张图片](http://img.e-com-net.com/image/info8/345a579e3a12459ba9a4eff8121df35d.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第13张图片](http://img.e-com-net.com/image/info8/9bee4b7830f34572b72e58c2c3f9fffa.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第14张图片](http://img.e-com-net.com/image/info8/b40e595fa5584658b4580edd3afddb4d.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第15张图片](http://img.e-com-net.com/image/info8/129931ce707645dda054935fe8d842a0.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第16张图片](http://img.e-com-net.com/image/info8/555e2ad460cd4e468be687f04ae5e140.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第17张图片](http://img.e-com-net.com/image/info8/d0f0622a78744e1e854f73e0d5313454.png)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第18张图片](http://img.e-com-net.com/image/info8/4f9fd19776fc4955bbc4e7fa9b79d4e3.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第19张图片](http://img.e-com-net.com/image/info8/ed55539b28db4e1c96ec24fcfc619629.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第20张图片](http://img.e-com-net.com/image/info8/98332248deba47bf96b5ea89e25af9ab.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第21张图片](http://img.e-com-net.com/image/info8/85687625f13f44fb9fc9536c92c9b228.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第22张图片](http://img.e-com-net.com/image/info8/128a1f70b05847ab858044f32f7e1712.jpg)
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]_第23张图片](http://img.e-com-net.com/image/info8/4d630b3d07464783a818d1d61c18c00e.jpg)