【算法】归并排序

目录结构：

contents structure

1. 简介
2. 归并排序的时间复杂度化
3. 归并排序的空间复杂度
4. 总结

1. 简介

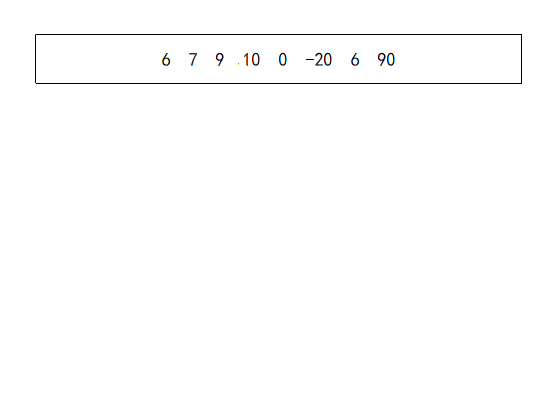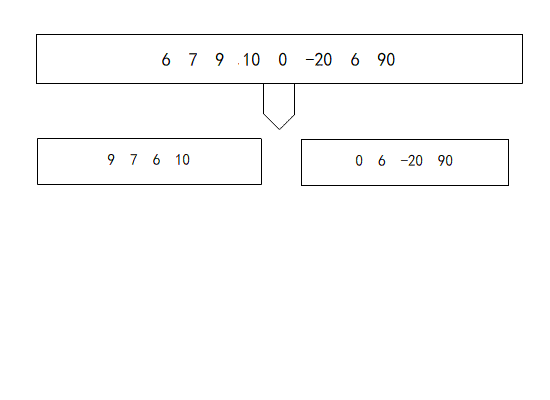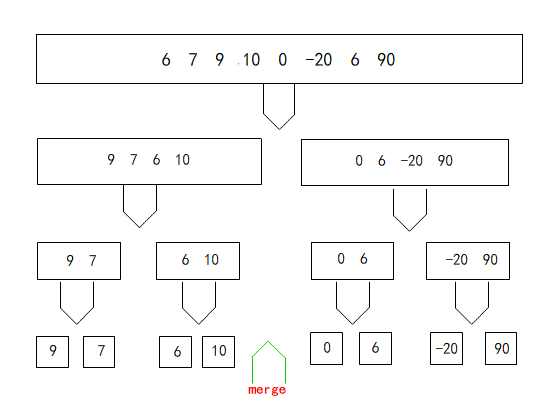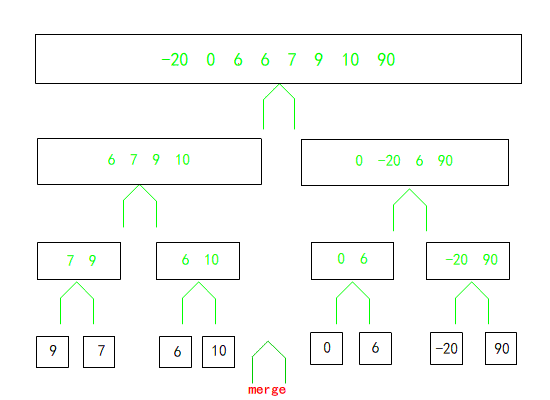
归并排序（MergeSort） 和快排的思想有相似之处。都是采用分治的思想，也就是，首先在一个数组中选择一个基准点，把数组分成两半，然后再对每一半再进行排序，递归直到所有数据都排好序。归并排序取分割点都是在数组的最中间，而且归并的过程也是采用了一个额外的数组变量来周转实现的。

首先先用C语言实现一个归并排序的过程。

#include 

int temp_array[];        //临时数组

void print(int*,int,int);
void merge(int*,int,int,int,int);
void mergeSort(int*,int,int);

int main () 
{
    int arr[] = {9,7,6,10,123,100,8,-1,0,6,-20,90,00,-110,31};
    size_t n = sizeof (arr) / sizeof (int);  //获取数组的长度
    //初始化数组，数组的长度为n，这里需要分配和排序数组一样的长度即可。
    //因为在归并过程中，可能用到的最大长度也就是n.
    memset (temp_array, 0, n * sizeof (int));
    
    //进行归并排序
    mergeSort (&arr, 0, n-1);
    
    print(&arr,0,n);
    
    return 0;
}
void mergeSort (int *arr, int begin, int end)
{
    if (begin >= end)
        return;
    
    //获取中间元素的下标
    int middle = (begin + end) / 2;
    
    int left_begin = begin;
    int left_end = middle;
    int right_begin = middle + 1;
    int right_end = end;
    
    //对左边进行排序
    mergeSort (arr, left_begin, left_end);
    
    //对右边进行排序
    mergeSort (arr, right_begin, right_end);
    
    //将左右两边排好序的序列汇总成一个序列
    merge (arr, left_begin, left_end, right_begin, right_end);
}
void merge (int *arr, int left_begin, int left_end, int right_begin, int right_end)
{
    size_t index = 0;
    
    //得到左边排好序的范围
    int left_index = left_begin;
    int left_index_max = left_end;
    
    //得到右边排好序的范围
    int right_index = right_begin;
    int right_index_max = right_end;
    
    //将两个范围的数据，按照升序，汇总到temp_array变量中。
    //左边和右边肯定有一边先退出条件，而另一边剩下的数据，是已经排好序的，
    //因此只需要将剩下的数据追加到temp_array即可。
    //比如：[1,4,5] 和 [1,3,7,8]
    while (left_index <= left_index_max && right_index <= right_index_max)
    {
        int left_val = arr[left_index];
        int right_val = arr[right_index];
        
        if (left_val < right_val)
        {
            temp_array[index++] = left_val;
            ++left_index;
        }
        else
        {
            temp_array[index++] = right_val;
            ++right_index;
        }
    }
    
    //比如: [1,4,5] 和 [1,3,7,8]
    //经过上面的合并，左边的数组先退出，这时候temp_array=[1,1,3,4,5]
    //右边还剩下[7,8], 只需要附加到temp_array末尾即可[1,1,3,4,5,7,8]
    if (left_index > left_index_max)  //左边先退出条件，将右边的数据追加到temp_array
        while (right_index <= right_index_max)
            temp_array[index++] = arr[right_index++];
    else  //右边先退出条件, 将左边的数据追加到temp_array
        while (left_index <= left_index_max)
            temp_array[index++] = arr[left_index++];
    
    //此时temp_array中的数据是排好了序的
    //最后将临时数组temp_array[0,right_end]中的数据，复制到arr中
    int arr_index = left_begin;
    int arr_index_max = right_end;
    size_t temp_index = 0;
    while (arr_index <= arr_index_max)
        arr[arr_index++] = temp_array[temp_index++];
}
void print(int *arr, int start, int end)
{
    for(int index=start; index < end; ++index)
        printf("%d ",arr[index]);
}

点我在Online GDB在线编译， 是不是上面的代码不太好理解，别担心，下面笔者制作了一张gif图片，可以更加形象理解归并排序的过程。

 

 

2. 归并排序的时间复杂度

上面讨论了归并排序的实现过程和理论基础，接下来继续讨论归并排序的时间复杂度。归并排序和快速排序相似，接下来深入分析一下归并排序的时间复杂度，由于归并排序每次取的都是数列最中间的位置，于是我们可以得出如下的表达式：

T(n)  = T(n/2) + T(n/2) + n

这个表达式和快排最优情况下的表达式一样，这里我就不再解一遍了，详情请移步快速排序最优时间复杂度。 解上面表达式最终可以得到时间复杂度为： n logⁿ. 

 

因为归并排序总是取的最中间的位置，所以无论排序的数列是什么样的，数列的排序都只有一种情况。换句话说，归并排序的最差，最优，平均时间复杂度都是O(n logⁿ)。

 

3. 归并排序的空间复杂度

 上面讨论了时间复杂度，接下来讨论空间复杂度，这里的空间复杂度就比较简单了，因为整个算法只声明了一个额外的变量 temp_array ，大小为n。所以总的空间使用的空间，就是temp_array所占用的空间 加上 递归时压入栈的空间，也就是 n + logⁿ, 因此归并的空间复杂度就是O(n).

 

4. 总结

这篇文章写的比较短，主要是省略了归并排序时间复杂度的推算，因为它和 快排最优情况下的时间复杂度推算 是一样的。而归并的空间复杂度也是比较简单的。最后，归并排序是一种稳定的算法，而快排是一种不稳定的算法（比如：1140，如果基准点选首元素，那么最终的结果第一个1和第二个1就会互调位置，因此不稳定）。在选择归并和快排的时候，需要综合它们的时间复杂度，空间复杂度 和 稳定性 再做选择。