本篇内容为视频笔记,视频地址为:https://www.bilibili.com/video/BV1Ut41197TE?from=search&seid=17921312669232031384
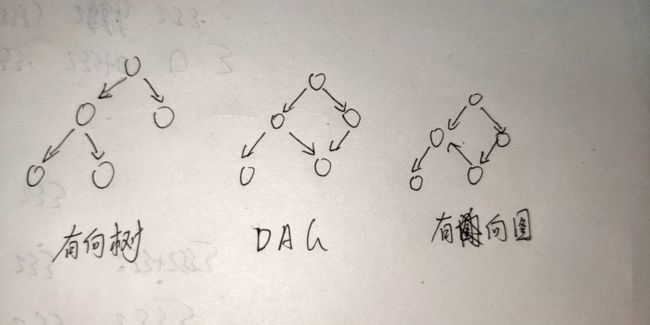
一,有向无环图
定义:无环的有向图,简称 DAG
有向无环图常用于描述一个工程或者系统的进行过程。(通常将计划,施工,生产,程序流程等当成一个工程)
一个工程可以分为若干子工程,只要完成这些子工程(活动),就可以完成整体工程。
那么这些工程有两种表示方法:AOV网 和 AOE网
AOV 网:(解决 拓扑排序 问题)
用一个有向图表示工程的各子工程及其相互制约的关系,其中 顶点表示活动,弧表示活动之间的优先制约关系,
称这种有向图为 顶点表示活动的网,简称 AOV
AOE 网:(解决 关键路径 问题)
用一个有向图表示工程的各子工程及其相互制约的关系,其中 弧表示活动,顶点表示活动的开始和结束
称这种有向图为 边表示活动的网,简称 AOE
二,AOV 网的特点
1,若从 i 到 j 有一条路径,则 i 是 j 的前驱 ,j 是 i 的后继;
2,若 < i , j > 是网中的有向边,则 i 是 j 的直接前驱 ,j 是 i 的直接后继
3,AOV 网不允许有 回路,因为如果存在回路的话,则说明 某项活动 是以自己为先决条件的,
这是荒谬的。
三,拓扑排序
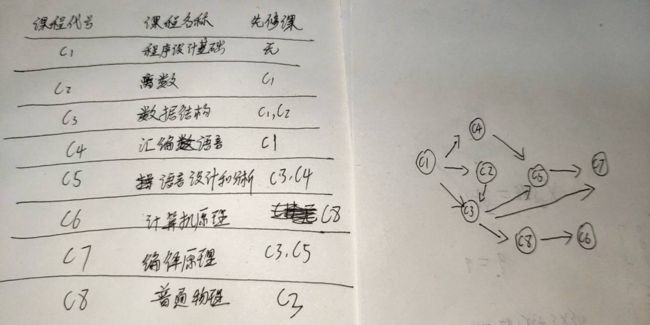
① 例题:排课表
随便画的,和原来不一样,意思一下。
② 拓扑有序序列
在 AOV 网没有回路的前提下,我们将全部活动排成一个线性序列,使得 AOV 网有弧
则在这个序列中,i 一定在 j 的签名,具有这种性质的线性序列称为 拓扑有序序列,相应的算法 称为
拓扑排序。
③ 拓扑排序 的方法
1,在有向图中 任何选一个没有前驱的 顶点 且输出它。
2,从图中删除 该顶点 及 所有以它为尾的弧。
3,重复上述两步,直至全部顶点均输出 或者 图中不存在 无前驱的顶点 为止
注意:输出的即为拓扑序列,且拓扑序列不唯一
④ 拓扑排序的一个应用
检查 AOV 网 是否存在 环
对于有向图构造其顶点的 拓扑有序序列,若网中所有顶点都在他的拓扑有序序列中,则该 AOV 网 中
必定不存在 环。
============ ========= ======== ====== ===== ==== === == =
一上高城万里愁,蒹葭杨柳似汀洲。
溪云初起日沉阁,山雨欲来风满楼。
鸟下绿芜秦苑夕,蝉鸣黄叶汉宫秋。
行人莫问当年事,故国东来渭水流。