摄像机模型（内参、外参）

摄像机模型（内参、外参）

本人邮箱：[email protected]，欢迎交流讨论，
欢迎转载，转载请注明网址http://blog.csdn.net/u010128736/

一、针孔模型

  下图是针孔摄像机的基本模型。平面π称为摄像机的像平面，点 Oc 称为摄像机中心（或光心），f成为摄像机的焦距， Oc 为端点且垂直于像平面的射线成为光轴或主轴，主轴与像平面的交点p是摄像机的主点。

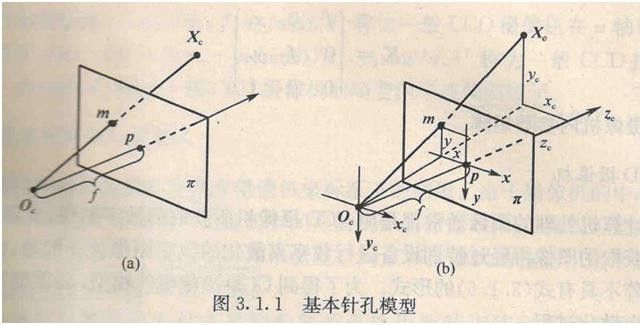
  如图所示，图像坐标系为o-xy，摄像机坐标系为 Oc−xcyczc 。记空间点 Xc 在摄像机坐标系中的齐次坐标为：

Xc=(xc,yc,zc,1)T

它的像点m在图像坐标系中的齐次坐标记为

m=(x,y,1)T

根据三角形相似原理，可得：

⎧⎩⎨x=fxczcy=fyczc

即：

zcm=⎡⎣⎢fxfy1⎤⎦⎥=⎡⎣⎢f000f0001000⎤⎦⎥Xc

由于是齐次坐标，可以记为

m=PXcP=diag(f,f,1)(I,0)

二、主点偏离图像中心

  上面讨论的是理论情况，但实际情况中，主点可能不是图像坐标系原点（这里定义为图像中心）。若主点在图像坐标系中坐标为

p=(x0,y0,1)T

则

P=K(I,0)=⎡⎣⎢f000f0x0y01000⎤⎦⎥

三、CCD摄像机

1、数字离散化

  通常我们获取得到的图像是CCD摄像机采集的数字图像，CCD相机是将图像平面的点进行数字离散化。嘉定CCD摄像机数字离散化后的像素是一个矩形，矩形的长与宽分别为dx，dy，则设像素坐标为 (u,v,1)T ，即

⎡⎣⎢uv1⎤⎦⎥=⎡⎣⎢⎢⎢⎢⎢1dx0001dy0001⎤⎦⎥⎥⎥⎥⎥⎡⎣⎢xy1⎤⎦⎥

K=⎡⎣⎢fx000fy0u0v01⎤⎦⎥

K为CCD的内参数矩阵，其中fx=f/dx，fy=f/dy称为CCD摄像机在u轴和v轴方向上的尺度因子， (u0，v0)T=(x0/dx，y0/dy)T 为CCD摄像机的主点。

2、倾斜因子

  由于工艺，CCD存在一个倾斜因子s， s=−fcyanθ/dx 。所以更一般的表示为

⎡⎣⎢uv1⎤⎦⎥=⎡⎣⎢⎢⎢⎢⎢⎢1dx00−ctanθdxsinθdy0001⎤⎦⎥⎥⎥⎥⎥⎥⎡⎣⎢xy1⎤⎦⎥

K=⎡⎣⎢fx00sfy0u0v01⎤⎦⎥=⎡⎣⎢⎢⎢⎢⎢⎢fdx00−fctanθdxfsinθdy0(x0−y0ctanθ)dxy0sinθdy1⎤⎦⎥⎥⎥⎥⎥⎥

四、外参数矩阵

  我们一般描述一个三维点，由于相机可能一直在运动，所以我们并不是基于摄像机坐标系下对其描述。我们通常是在世界坐标系下进行描述。世界坐标系与相机坐标系之间的关系可以用旋转矩阵和平移向量来描述。

如图所示，零空间点在世界坐标系下的坐标为 X=(x,y,z,1)T ，相机坐标系为 Xc=(xc,yc,zc,1)T ，两者关系为：

Xc=[R0T−RC~1]X

R(I,-C)为相机的外参数矩阵。其中R为旋转矩阵，令平移向量t为：

t=−RC~

五、补充

1、摄像机中心

  设相机在世界坐标系下的齐次坐标为C，则

PC=KR(I,−C~)[C~1]=KR(C~,−C~)=0

令P=(H,p4)，其中H为P的前三列所构成的3×3矩阵，p4是P的第四个列向量，所以

C=[−H−1p41]

2、坐标原点

  记 P=(p1,p2,p3,p4) ，其中 pj 为P的j列向量。世界坐标系的原点 X=(0,0,0,1)T ，所以其图像坐标为

s0m0=PX=(p1,p2,p3,p4)⎡⎣⎢⎢⎢0001⎤⎦⎥⎥⎥=p4

所以P矩阵的第4列向量是世界坐标原点对应的图像上的齐次坐标。

3、坐标轴方向

  世界坐标系3个坐标轴方向的图像，3个坐标轴与无穷远平面交点分别为 X=(1,0,0,0)T，Y=(0,1,0,0)T，Z=(0,0,1,0)T ，所以他们的图像坐标分别为：

s1m1=PX=p1s2m2=PY=p3s3m3=PZ=p3

即摄像机矩阵P的前3个列向量分别是世界坐标系3个坐标轴方向的图像点的齐次坐标。

参考

1、《计算机视觉中的数学方法》，吴福朝
2、《计算机视觉中的多视图几何》，剑桥大学出版社