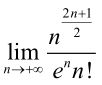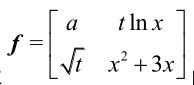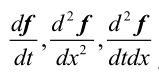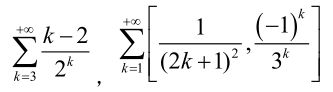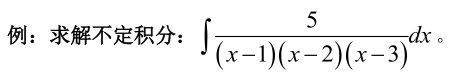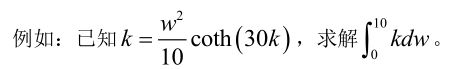Matlab符号计算与方程组求解

一、符号计算

1、符号计算特点

        1、计算精确：符号计算基于数学公式、定理并通过一系列推理、演绎得到方程的解或者数学表达式的值。对操作对象不进行离散化和近似化处理。

        2、可应用范围有限：实际科研和生产中遇到的问题绝大多数都无法获得精确的符号解，这时我们不得不求助数值计算。

        3、对待符号计算态度：用其来完成公式推导和解决简单的对计算时效性要求不高的问题，综合符号计算和数值计算各自的优点，视问题特点混合使用符号计算和数值计算。

2、符号对象和符号表达式

        1、符号对象的创建：要生成一个符号对象，可以利用sym以及syms函数，sym可以生成单个符号对象，而syms可以生成多个符号对象，符号对象的运算是完全精确的，没有舍入误差。例如：a = sym(‘5’);  syms b c d;。

        2、符号表达式：创建了符号对象，我们就可以创建各种各样的符号表达式。譬如，创建符号变量a, b, c后如下都是符号表达式：

         z1 = a+b+c;

         z2 = sin(a+b+c);

         z3= a^b*gamma(c);

        确定一个符号表达式中的符号变量可以用findsym函数：

         findsym(expr);

         findsym(expr, n);

        第一种用法是确认表达式expr中所有自由符号变量，第二种用法是从表达式expr中确认出距离x最近的n个符号变量。这个最近距离指的是变量第一个字符和x的ASCII码值之差的绝对值，差绝对值相同时，ASCII码值大的字符优先。findsym是老版本中的方法，新版本将使用symvar函数代替：symvar(expr);。

         3、运算符：MATLAB采用了重载（Overload）技术，使得用来构成符号表达式的运算符，无论在拼写还是在使用方法上，都与数值计算中的算符完全相同。譬如“+”，“-”，“*”，“\”，“/”，“^”等。

        符号对象的比较中，没有“大于”、“大于等于”，“小于”，“小于等于”的概念，而只有是否“等于”的概念，即“==”与“~=”。如果要判断两个符号数值的大小一般来说有两种办法，一种是利用double将其转化成数值型的，另一种是利用sort+“==”或“~=”。譬如下面代码：

>> a = sym('2');
>> b= sym('3');
>>double(a)> sa = sort([b,a])
sa =
[ 2, 3]
>>a==sa(1)
ans =
     1

从上述代码可以看出，上述两种方法都间接实现了判断大小。

        4、符号计算与数值计算结合：利用符号计算得到结果时，有时需要将其转化成数值型的以便后续数值计算利用。通过符号计算得到一个表达式时，想把它转化成关于其中某个变量的数值函数。

        很多时候我们需要求符号表达式在不同的参数值下的具体值，说通俗点就是如何把具体的参数代入符号表达式。这时候可以利用eval和subs函数或者转化成匿名函数。

程序实例：

clc;
clear;
 
% 将符号变量转化成数值
format long;
% 可供使用的一些方法
% 这里a是符号变量，a1--a4是数值变量
a = vpa(pi,30); %3.14159265358979323846264338328
a1 = double(a); %3.141592653589793
a2 = eval(a); %3.141592653589793
a3 = single(a); %3.1415927
a4 = int8(a); % 3
 
 
% 很多时候我们需要求符号表达式在不同的参数值下的具体值，
% 说通俗点就是如何把具体的参数代入符号表达式。这时候可以利用eval和subs函数或者转化成匿名函数
 
% 如下的例子：求函数：f =sin( x^x / (x^2/exp(x)) );  其二阶导数在x = 1处的值。
syms x;
f = sin(x^x / x^2/exp(x));
% 利用符号计算求f(x)的二阶导数
% diff函数用于求导数或者向量和矩阵的比较。
% 如果输入一个长度为n的一维向量，则该函数将会返回长度为n-1的向量，向量的值是原向量相邻元素的差
d2f = diff(f, x, 2);
 
% 第一种方法：利用subs函数求d2f在x=1时的值。
d2fx1 = subs(d2f, x, 1);  % d2fx1 = 2.2082
 
% 第二种方法：x赋值1后，利用eval函数求d2f在x = 1时的值
x = 1;
d2_fx1 = eval(d2f); %d2_fx1 = 2.2082
   
% 第三种方法：将d2f转化成匿名函数，求其在x = 1时的值
% vectorize的含义就是将乘转成点乘等。  '*' -> '.*'； '/' -> './'； '^' -> '.^'； 最后再将替换结果中的“..”删除一个"."。
F = eval(['@(x)',vectorize(char(d2f))]);
F(1)  % ans=  2.2082

二、极限、导数和级数的符号计算

1、求的极限。

clc;
clear;
 
% 求极限
syms n;
% limit函数用于求极限运算。假如y=f(x)，limit(y)表示x→0时的极限，limit(y,x,a)表示x→a时的极限
% MATLAB中gamma函数即数学上的gamma函数，当n为正整数时，有如下性质：gamma(n+1) = n!
limit( n^(n+1/2) /( exp(n)*gamma(n+1)), n,inf)  % ans= 1/(2*pi)^(1/2)

2、求的导数，。

% 求导数
syms a t x;
f = [a, t*log(x); sqrt(t), x^2+3*x];
% 矩阵f对t的一阶导数
dfdt = diff(f,t);  % dfdt = [ 0, log(x);   1/(2*t^(1/2)), 0 ];
 
% 矩阵f对x的二阶导数，由于是x，而f中含有x变量，故x可以省略
dfdx2 = diff(f,2);  % dfdx2 =[ 0, -t/x^2;  0, 2 ];
 
%求二阶混合导数
dfdtdx = diff(diff(f,t),x); %dfdtdx =[ 0, 1/x;  0, 0 ];

3、求无穷级数：

% 求级数
syms k;
f1 = symsum( (k-2)/2^k, k, 3, inf);  % f1 = 1/2
 
A = [1/(2*k+1)^2, (-1)^k/3^k];
f2 = symsum(A, k, 1, inf); % f2= [ pi^2/8 - 1, -1/4]

三、求解方程

        求解方程通常有两种方法，符号求解和数值求解。

1、solve

        通常在不确定方程是否有符号解的时候，推荐先使用solve进行尝试，因为solve相比于数值求解来说，它不需要提供初值，并且一般情况下能够得到方程的所有解。对于一些简单的超越方程，solve还能够自动调用数值计算系统给出一个数值解。

        solve的调用形式：

        sol = solve(eq)

        sol = solve(eq, var)

        sol = solve(eq1, eq2, …, eqn)

        sol = solve(eq1, eq2, …, eqn, var1, var2, …, varn)

        eq为符号表达式，var为指定的要求解的变量。如果不声明要求解的变量(第一和第三种形式)，则matlab自动按默认变量进行求解，默认变量可以由symvar(eq)确定。

例：求解方程组: x+y=1, x-11y=5

% 使用solve函数求解方程
% 例：求解方程组: x+y=1, x-11y=5
clc;
clear;
 
% 声明符号变量
syms x y;
% 定义方程
eq1 = x + y -1;
eq2 = x - 11*y - 5;
% 调用solve求解方程组
% （solve函数的参数包括方程表达式，以及要求解的变量，这里变量是可选参数，不指定时matlab自动按默认变量进行求解）
% 这时候solve求得的解通过结构体的形式赋值给sol，然后再通过x=sol.x和y=sol.y分别赋值给x和y。
sol = solve(eq1, eq2, x, y);
x = sol.x;
y = sol.y;
% 也可以直接使用：
% [x,y] = solve(eq1, eq2, x, y);
 
% 使用double将符号解转换为数值解
value_x = double(x);
value_y = double(y);

        需要注意，等式左边接收参数时应当按字母表进行排序，否则MATLAB不会自动识别你的参数顺序，比如：

        [x, y] = solve(eq1, eq2, x, y)

        [y, x] = solve(eq1, eq2, x, y)

        solve会把答案按字母表进行排序后进行赋值，x解赋值给第一个参数，y解赋值给第二个参数，那么对于第二种形式，实际上最终结果是变量y存储了x的解而变量x存储了y的解。

        由于是符号求解，有时候得到的解是一大串式子(符号求解无精度损失，所以MATLAB不会自动将答案转化为浮点数)，这时候可以用vpa或者double函数将结果转换为单一的数。

         另外很多人习惯对于solve的参数采用字符型输入，这种方式有几个弊端，首先就是程序的调试，一旦式子输入有误(最常见的就是括号的配平)，将会对程序调试带来很大的困难。

        其次是采用字符型输入时，对变量的赋值并不能传入方程，以x+y*sin(x)=1这个方程为例：y = 1;  sol = solve('x+y*sin(x)=1','x')，MATLAB会返回一个空解，但是对于sym型输入：syms x;  y=1;  eq=x+y*sin(x)-1;  sol=solve(eq,x); 能够得到sol=0.5109734293885691，其中的区别就在于char型输入尽管在solve前对y有一个赋值，但solve求解时依然会将y当作一个未赋值的常数。 

        最后，在高版本solve已经不支持char型参数输入，因此应该放弃使用这种方法。

 

2、fzero

        然而在很多情况下solve并不能求得方程的解析解，这时就可以采用数值法求解。

        数值求解法包括fzero和fsolve，其区别在于fzero只适用求解一元函数零点，而fsolve适用于求解多元函数零点(包括一元函数)。当求解一元函数零点时，推荐优先使用fzero，原因是fzero求解一元方程往往更容易，因为它不仅支持提供初值的搜索，还支持在一个区间上进行搜索。

        fzero的常用形式：

        x = fzero(fun, x0);

        [x, fval] = fzero(fun, x0);

        其中fun为函数句柄，x0为搜索初值，fval为求解误差。

        如果方程有多个零点时，fzero只能根据提供的初值求得最靠近初值的一个零点，如果希望求得多个零点的话，那么只能够通过改变初值来得到不同的零点。

        对于零点的选取，目前来说没有什么比较好的办法，只能够通过分析方程的性质，或者通过作图的方法去寻找一个比较靠近零点的初值。另外，fzero能够提供区间搜索，注意区间两端的端点函数值符号需要反向。

以一元方程sin(x)+cos(x)^2=0为例：

clc;
clear;
 
% fzero只适用求解一元函数零点
% 求sin(x)+cos(x)^2=0的零点
% 这里采用匿名函数，也可以使用函数文件形式
y = @(x)sin(x)+cos(x).^2;
% 1为搜索初值，fval为求解误差
[x, fval] = fzero(y, 1);
 
% fzero在[3, 4]这个区间搜索初值
[t, eval] = fzero(y,[3 4]);

3、fsolve

        fsolve可以求解多元方程，用法和fzero类似。

        fsolve的常用形式：

        x = fsolve(fun, x0);

        [x, fval] = fsolve(fun, x0);

        其中fun为函数句柄，x0为搜索初值，fval为求解误差。

例：求解方程组x+y=1, x-11y=5

% fsolve函数求解多元函数
% x+y=1,  x-11y=5
eq = @(x)[x(1)+x(2)-1;  x(1)-11*x(2)-5];
[sol, err] = fsolve(eq, [1,1]);

        这里对于方程的的输入需要采用矩阵的形式，其中x(1)代表x，x(2)代表y。有时候变量较多时可能会容易混淆，这里提供另一种方法，采用符号变量形式再利用matlabFunction转化为函数句柄：

% 采用符号变量形式再利用matlabFunction转化为函数句柄
syms x y
eq1 = x+y-1;
eq2 = x-11*y-5;
% 将符号函数转化为函数句柄
eq1 = matlabFunction(eq1);
eq2 = matlabFunction(eq2);
eq = @(x)[eq1(x(1), x(2)); eq2(x(1), x(2))];
[sol2, err2] = fsolve(eq, [1,1]);

        效果与之前相同，但不容易出错。求得的解以矩阵形式返回给sol，即sol的第一个值是匿名函数的第一个输入参数值x，sol的第二个值是匿名函数的第二个输入参数值y。

 

4、vpasolve

        vpasolve是R2012b引进的函数，可以求解一元或多元函数零点。相比于fzero和fsolve来说，vpasolve最大的一个优点就是不需要提供初值，且能够自动搜索指定范围内的多个解。

        vpasolve调用形式：

        S = vpasolve(eqn);

        S = vpasolve(eqn, var);

        S = vpasolve(eqn, var, init_guess);

        ___ = vpasolve(___, Name, Value);

        其中eqn是符号方程，var为需要求解的变量，也可以不提供(第一种形式，这是默认求解变量由symvar(eqn)求得)，init_guess为搜索初值，Name, Value为一些选项控制。

例：对于多项式方程，vpasolve能够给出所有解：

syms x;
vpasolve(4*x^4 + 3*x^3 + 2*x^2 + x + 5 == 0, x);
ans =
        - 0.88011 - 0.76332i
        0.50511 + 0.81599i
        0.50511 - 0.81599i
        - 0.88011 + 0.76332i

对于非多项式方程，vpasolve给出它找到的第一个解：

syms x;
vpasolve(sin(x^2) == 1/2, x);
ans =
        -226.94

这时可以提供搜索初值，来改变它找到的解：

syms x;
vpasolve(sin(x^2) == 1/2, x,100);
ans =
        99.996

可以指定搜索范围，但不同于solve，solve指定求解范围是用assume函数，vpasolve则是直接在输入参数中指定：

syms x;
vpasolve(x^8 - x^2 == 3, x, [-Inf Inf]); %实数范围内求解

最后，vpasolve一个很强大的用法，将‘random’选项设置为true可以直接搜索指定范围内不同解：

syms x;
f = x-tan(x);
for n = 1:3
        vpasolve(f,x,'random',true);
end

5、左除”\”与右除”/”

        在MATLAB环境中，强烈建议使用左除”\”或者右除”/”解线性方程组。左除和右除是根据除号左侧还是右侧是分母而定的，方程系数矩阵在未知数左侧，则用左除，反之用右除。使用左除”\”或者右除”/”的好处是因为其对线性方程(组)的广泛适用性，当未知数个数大于方程个数的时候，左除或右除会给出方程的特解，结合null函数，可以得到通解。当未知数个数小于方程个数的时候，左除或右除会给出方程的最小二乘解。

 

四、求解积分

        求解积分与求解方程相同，也有两种方法，符号求解和数值求解。与数值积分相比，符号积分具有指令简单，占用机时长等特点，因此一般复杂的积分运算都采用数值积分函数来计算。但某些情况下，特别是一些简单的上下限为函数的多重积分，用符号积分计算会比调用数值积分函数计算简单方便许多。

1、int

        int是符号积分求解器，调用形式简单，但是功能非常强大。

        int常用形式：

        intf = int(expr, var)   %不指定积分上下限，即求解不定积分

        intf = int(expr, var, a, b)    %指定积分上下限，即求解定积分

        上述调用格式中var可以省略，var省略时，积分将针对findsym确定的变量来进行。a, b作为积分上下限，实际输入中可以为数值符号或者字母符号。

% int求积分
syms x;
% 这里没有制定区间，求解的是不定积分
f = 5 / ((x-1)*(x-2)*(x-3));
F = int(f, x);  % F = (5*log(x^2 - 4*x + 3))/2 -5*log(x - 2)

syms y;
f = x / (1 + y^2);
F = int(f, y, 0, 1);  % F = (pi*x)/4

但是大多情况下int都得不到解析解，这时候就可以采用数值积分。

 

2、integral

        integral是2012a引进的一个函数，一元函数积分中功能最为强大，调用形式和quad基本一致：

        q = integral(fun, xmin, xmax);

        q = integral(fun, xmin, xmax, Name, Value);

        其中fun为函数句柄，xmin为积分下限，xmax为积分上限，Name和Value是一些选项控制，包括误差、向量化积分等等。integral配合fzero可以求解无法显式表达的函数的定积分。

% integral求数值积分
q = @(k, w)w.^2 / 10.*coth(30*k)-k;
v = @(w)fzero(@(k)q(k,w), 1e3);   % 利用fzero求解k, 相当于显式表达k
value = integral(v, 0, 10, 'ArrayValued', 1);

3、trapz

        trapz是基于梯形法则的离散点积分函数。调用形式：

        I = trapz(x, y);

        其中x和y分别是自变量和对应函数值。

例：sin(x)在[0, pi]的积分：

% trapz求离散点积分
t = linspace(0, pi, 1e3);   %生成[0, pi]内的一系列离散点
y = sin(t);
I = trapz(t, y);