p1095 约瑟夫问题10E100版 （Vijos）

描述

n个人排成一圈。从某个人开始，按顺时针方向依次编号。从编号为1的人开始顺时针“一二一”报数，报到2的人退出圈子。这样不断循环下去，圈子里的人将不断减少。由于人的个数是有限的，因此最终会剩下一个人。试问最后剩下的人最开始的编号。

格式

输入格式

一个正整数n，表示人的个数。输入数据保证数字n不超过100位。

输出格式

一个正整数。它表示经过“一二一”报数后最后剩下的人的编号。

样例1

样例输入1

9

样例输出1

3

限制

各个测试点1s

提示

样例说明

当n=9时，退出圈子的人的编号依次为：
2 4 6 8 1 5 9 7
最后剩下的人编号为3

来源

Matrix67 根据经典问题改编

分析

约瑟夫环问题

原问题：
已知有 n 个人，围成一个圈，现在开始报数，将报数为 q 的人从这个环中去除掉，然后在接下来的 n-1 个人中，从第 q+1 个人开始再从头报数，再去除第 q 个人……

在这道题中 q = 2

根据公式
n=(2k+t) n = ( 2 k + t ) ，(其中 2k 2 k 中，k 的取值保证了 2k 2 k 距离 n 最近)
此时：最终剩下的人的编号应该是 2∗t+1 2 ∗ t + 1

注意
要计算 t ，只需要将 n 的 2 进制数中的第一个 1 变成 0 就行啦。。。

如何做到将第一位变成 0 呢？

将 1<<n.bitLength−1 1 << n . b i t L e n g t h − 1 ，会得到一个数 b，然后将 b 取反得到 b’
此时，将 n 与 b’ 进行与操作 （n&b’）得到的数就是 t 了~~ (´・ω・`)

代码

因为 n 的长度不超过 100位(曾经看成了不超过100 … (´・ω・`) 慌了慌了~~)，所以我用的是 Java 的 BigInteger
比如：
对于数 11 ，11 的二进制数是 1011，那么 11 的 bitLength = 4，那么
1<<bitLength−1 1 << b i t L e n g t h − 1 = 1000(当然啦，这是二进制)，这时候我们对 1000
取反得到 0111
将 0111 与 1011 进行与运算得到 1011 & 0111 得到的是 0011 即是 3，这是后
最后的人的编号就是 2*3+1 = 7 （即是我们要求的结果）

import java.math.BigInteger;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {

        Scanner cin = new Scanner(System.in);
        BigInteger n = cin.nextBigInteger();
        BigInteger t = BigInteger.valueOf(1).
            shiftLeft(n.bitLength() - 1); 
        System.out.println(
            (t.not().and(n)).
            multiply(new BigInteger("2"))
            .add(new BigInteger("1"))
            );
    }
}

接下来我们总结下关于约瑟夫环问题的解决方案

参考大佬博客(´・ω・`)
递归思想解决Josephus问题
约瑟夫环问题详解

问题背景

       约瑟夫是犹太军队的一个将军，在反抗罗马的起义中，他所率领的军队被击溃，只剩下残余的部队40余人，他们都是宁死不屈的人，所以不愿投降做叛徒。一群人表决说要死，所以用一种策略来先后杀死所有人。于是约瑟夫建议：每次由其他两人一起杀死一个人，而被杀的人的先后顺序是由抽签决定的，约瑟夫有预谋地抽到了最后一签，在杀了除了他和剩余那个人之外的最后一人，他劝服了另外一个没死的人投降了罗马……

我们知道，n 是总人数，q 是每次的报数……（假设编号是从 0 -> n-1 ）
那我们对 n 和 q 的取值进行分析：

1. 当q = 2，n 是 2^k 时

#n = 2
0 ， 1 ·······> 0 ····················································> 0
#n = 4
0 ，1 ，2 ，3 ·········> 0 ，2 ··································> 0
#n = 8
0 ，1 ，2 ，3 ，4 ，5 ，6 ，7 ···> 0 ，2 ，4 ，6 ··> 0 ，4 ··> 0
…….

由以上规律可知，当 n=2k n = 2 k , q = 2 时，活下来的人总是原始报数是 0 的人。
定义 Fq(n) F q ( n ) 是 n 个人，每次去掉第 q 个人的约瑟夫环问题最终结果：

则 F2(2k)=0 F 2 ( 2 k ) = 0

2. 当 q = 2，n 是 任意数时

我们假设此时 n = 11，如下图所示：

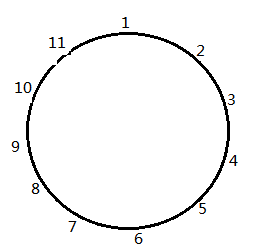
从 1 号开始报数，开始 2，4，6… 被删除…

此时，剩余的编号为 1，3，5，7，8，9，10，11（总共是 8 个数 = 23 2 3 ）
而在这 8 个数中，第一个开始报数的是 编号是 7 的人，如此：根据 F2(2k)=0 F 2 ( 2 k ) = 0
(这里的0是指第一个报数的人的编号)，此时 7 就是最终剩余的人的编号，
即 F2(11)=7 F 2 ( 11 ) = 7 .

由此可知，我们将任意数 n 可以转化成 2k+t 2 k + t ，也就是说 F2(n)=F2(2k+t) F 2 ( n ) = F 2 ( 2 k + t )
而最终所求的编号就是， 2∗t+1 2 ∗ t + 1
结论： F2(n)=F(2k+t)=2∗t+1 F 2 ( n ) = F ( 2 k + t ) = 2 ∗ t + 1
注意： t 的计算方法，将 n 的二进制的最高位 1 变为 0 后，就是我们要求的 t
如上所说的 11 -> 1011 -> 0011 -> 3，即 最后结果是 2*3+1 = 7

3. 当 q 是任意数，n 是任意数时

有两种解决方案：
1. 链表模拟解决
2. 递归思想解决

1.链表模拟

未完待续

2.递归思想

在 q!=2 q ! = 2 的情况下，n 是指总的人数，q 是指每次移除第 q 个人
Fq(n) F q ( n ) 表示 n 人构成的约瑟夫环，每次移除第 q 个人的解

只要找到 Fq(n) F q ( n ) 与 Fq(n−1) F q ( n − 1 ) 之间的关系，该问题就能够轻松求解了(´・ω・`)~~

首先假设初始情况是：

0,1,2,3,4,5…q-2,q-1,q,q+1…n-1,n ··············> 总共是 n 个人

移除第 q 个人（编号是 q-1 ）后变成了

0,1,2,3,4,5…q-2,q,q+1…n-1,n ················> 总共是 n-1 个人

接下来就需要从 第 q+1 个人（编号是 q ）开始报数……

将上一步的 n-1 个人的编号进行映射
q —–> 0
q+1 ->1
q+2 ->2
q+3 ->3
q+4 ->4
q+5 ->5
…
q-2 –>n-1

变换之后，变成了(n-1)个人报数，假设最终的胜利者是 x，那么，
根据这 n-1 个人的编号，对应的 n 个人的时候的编号是

0–>q
1–>q+1
2–>q+2
3–>q+3
…
x’–>q+x
…

那么从 n-1 变回 n 时的公式就是：x’ = (x+q) % n

所以： Fq(n)=(Fq(n−1)+q) F q ( n ) = ( F q ( n − 1 ) + q ) % n n 其中 Fq(1)=0 F q ( 1 ) = 0

#include  
using namespace std;

int main()
{
    int n;cin >> n >> q;
    int ans = 0; // Fq(1) = 0
    for(int i = 2;i <= n;i++) {
        ans = (ans + q)%i;
    }
    cout << ans + 1 << endl;
    return 0;
}