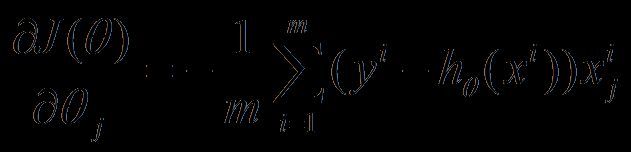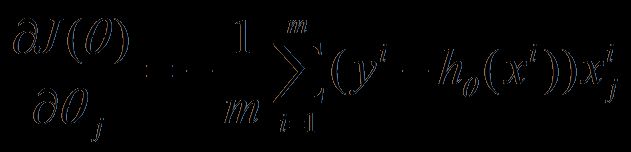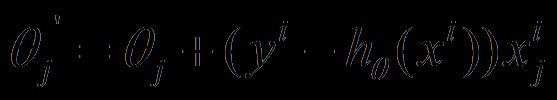人工智能之用excel和python实现一元二元函数梯度下降

梯度下降法和牛顿法的总结与比较

机器学习的本质是建立优化模型，通过优化方法，不断迭代参数向量，找到使目标函数最优的参数向量。最终建立模型

通常用到的优化方法：梯度下降方法、牛顿法、拟牛顿法等。这些优化方法的本质就是在更新参数。

一、梯度下降法

0、梯度下降的思想

通过搜索方向和步长来对参数进行更新。其中搜索方向是目标函数在当前位置的负梯度方向。因为这个方向是最快的下降方向。步长确定了沿着这个搜索方向下降的大小。

迭代的过程就像是在不断的下坡，最终到达坡地。
接下来的目标函数以线性回归的目标函数为例：

1、批量梯度下降法

2、随机梯度下降法

3.随机梯度下降和梯度下降的比较

批量梯度下降：1.是最小化所有样本的损失函数，最终得到全局最优解。

2.由于每次更新参数需要重新训练一次全部的样本，代价比较大，适用于小规模样本训练的情况。

随机梯度下降：1.是最优化每个样本的损失函数。每一次迭代得到的损失函数不是，每次每次向着全局最优的方向，但是大体是向着全局最优，最终的结果往往是在最优解的附近。

2.当目标函数是凸函数的时候，结果一定是全局最优解。

3.适合大规模样本训练的情况。

小批量梯度下降法

将上述两种方法作结合。每次利用一小部分数据更新迭代参数。即样本在1和m之间。

二、牛顿法

首先牛顿法是求解函数值为0时的自变量取值的方法。

利用牛顿法求解目标函数的最小值其实是转化成求使目标函数的一阶导为0的参数值。这一转换的理论依据是，函数的极值点处的一阶导数为0.

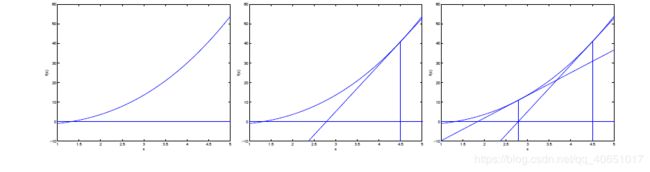
其迭代过程是在当前位置x0求该函数的切线，该切线和x轴的交点x1，作为新的x0,重复这个过程，直到交点和函数的零点重合。此时的参数值就是使得目标函数取得极值的参数值。

其迭代过程如下：

迭代的公式如下：

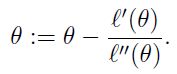
当θ是向量时，牛顿法可以使用下面式子表示：

其中H叫做海森矩阵，其实就是目标函数对参数θ的二阶导数。

三、牛顿法和梯度下降法的比较

1.牛顿法：是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。

收敛速度很快。

海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。

缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。

2.梯度下降法：是通过梯度方向和步长，直接求解目标函数的最小值时的参数。

越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。

一元函数梯度下降

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings

"""
对当前一维原始图像求最小点：
1、随机取一个点(横坐标为x)，设定阿尔法参数值。  
2、对这个点求导数 ,x =x - α*(dY/dx)。  
3、重复第二步、设置迭代 y的变化量小于多少时 不再继续迭代。
"""
# 导数
def h1(x):
    return 0.5 * 2 * (x-0.25)
X = np.arange(-4,4,0.05)
Y = np.array(list(map(lambda t: f1(t),X)))
Y

 
x = 4
alpha = 0.5
f_change = f1(x) # y的变化量
iter_num = 0 # 迭代次数
GD_X = [x] #保存梯度下降所经历的点
GD_Y = [f1(x)]
 
while(f_change > 1e-10) and iter_num<100:
    tmp = x - alpha * h1(x)
    f_change =  np.abs(f1(x) - f1(tmp))
    x = tmp
    GD_X.append(x)
    GD_Y.append(f1(x))
    iter_num += 1
    
print(u"最终结果为:(%.5f,%.5f)"%(x,f1(x)))
print(u"迭代过程中X的取值，迭代次数:%d" % iter_num)
print(GD_X)
 
%matplotlib inline
plt.figure(facecolor='w')
plt.plot(X,Y,'r-',linewidth=2) #第三个参数是颜色和形状，red圈就是ro-,red直线就是r-
plt.plot(GD_X, GD_Y, 'bo-', linewidth=2)
plt.title(u'函数$ y = 0.5 * (x-0.25)^2$;\n学习率%.3f;最终解:(%.3f,%.3f),迭代次数：%d'%(alpha,x,f1(x),iter_num))

二元函数梯度下降

1.导入基本库、数据，并为变量赋值

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data=np.genfromtxt('D:/面积距离车站数据.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,2]

2.定义系数初始值以及学习率和迭代次数

lr=0.00001
theta0=0
theta1=0
theta2=0
#定义最大迭代次数，因为梯度下降法是在不断迭代更新k与b
epochs=10000

#定义最小二乘法函数-损失函数（代价函数）
def compute_error(theta0,theta1,theta2,x_data,y_data):
    totalerror=0
    for i in range(0,len(x_data)):#定义一共有多少样本点
        totalerror=totalerror+(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
    return totalerror/float(len(x_data))/2
    #梯度下降算法求解参数
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
    m=len(x_data)
    for i in range(epochs):
        theta0_grad=0
        theta1_grad=0
        theta2_grad=0
        for j in range(0,m):
            theta0_grad-=(1/m)*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta2)+y_data[j])
            theta1_grad-=(1/m)*x_data[j,0]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
            theta2_grad-=(1/m)*x_data[j,1]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
        theta0=theta0-lr*theta0_grad
        theta1=theta1-lr*theta1_grad
        theta2=theta2-lr*theta2_grad
    return theta0,theta1,theta2

3.打印

#进行迭代求解
theta0,theta1,theta2=gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
print('结果：迭代次数：{0} 学习率：{1}之后 a0={2},a1={3},a2={4},代价函数为{5}'.format(epochs,lr,theta0,theta1,theta2,compute_error(theta0,theta1,theta2,x_data,y_data)))
print("多元线性回归方程为:y=",theta1,"X1+",theta2,"X2+",theta0)

4.画图

ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o')
x0=x_data[:,0]
x1=x_data[:,1]
#生成网格矩阵
x0,x1=np.meshgrid(x0,x1)
z=theta0+theta1*x0+theta2*x1
#画3d图
ax.plot_surface(x0,x1,z)
ax.set_xlabel('area')
ax.set_ylabel('distance')
ax.set_zlabel("Monthly turnover")
plt.show()

运行结果

最小二乘法法求解多元线性回归方程的python代码实现

代码如下：

#利用线性代数的矩阵模拟最小二乘法求解法求解多元线性回归方程的系数
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
%matplotlib inline
data = np.genfromtxt("D:/面积距离车站数据.csv",delimiter=",")
X1=data[0:10,0]#自变量温度
X2=data[0:10,1]#因变量销售量
Y=data[0:10,2]#自变量温度
#将因变量赋值给矩阵Y1
Y1=np.array([Y]).T
#为自变量系数矩阵X赋值
X11=np.array([X1]).T
X22=np.array([X2]).T
A=np.array([[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]])#创建系数矩阵
B=np.hstack((A,X11))#将矩阵a与矩阵X11合并为矩阵b
X=np.hstack((B,X22))#将矩阵b与矩阵X22合并为矩阵X
#求矩阵X的转置矩阵
X_=X.T
#求矩阵X与他的转置矩阵的X_的乘积
X_X=np.dot(X_,X)
#求矩阵X与他的转置矩阵的X_的乘积的逆矩阵
X_X_=np.linalg.inv(X_X)
#求解系数矩阵W，分别对应截距b、a1、和a2
W=np.dot(np.dot((X_X_),(X_)),Y1)
b=W[0][0]
a1=W[1][0]
a2=W[2][0]
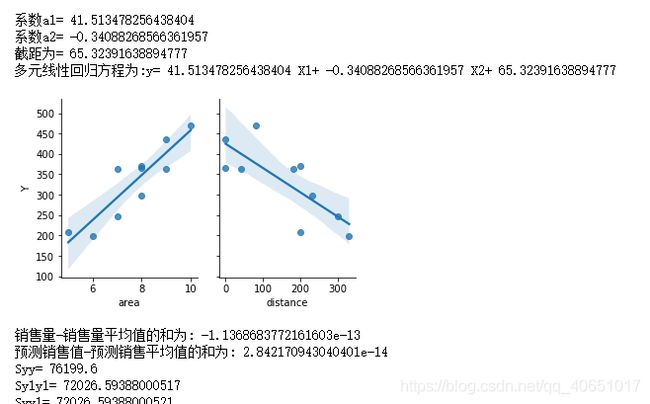
print("系数a1=",a1)
print("系数a2=",a2)
print("截距为=",b)
print("多元线性回归方程为:y=",a1,"X1+",a2,"X2+",b)
#画出线性回归分析图
data1=pd.read_excel('D:\面积距离车站数据.xlsx')
sns.pairplot(data1, x_vars=['area','distance'], y_vars='Y', height=3, aspect=0.8, kind='reg')  
plt.show() 
#求月销售量Y的和以及平均值y1
sumy=0#因变量的和
y1=0#因变量的平均值
for i in range(0,len(Y)):
    sumy=sumy+Y[i]
y1=sumy/len(Y)
#求月销售额y-他的平均值的和
y_y1=0#y-y1的值的和
for i in range(0,len(Y)):
    y_y1=y_y1+(Y[i]-y1)
print("销售量-销售量平均值的和为:",y_y1)
#求预测值sales1
sales1=[]
for i in range(0,len(Y)):
    sales1.append(a1*X1[i]+a2*X2[i]+b)
#求预测值的平均值y2
y2=0
sumy2=0
for i in range(len(sales1)):
    sumy2=sumy2+sales1[i]
y2=sumy2/len(sales1)
#求预测值-平均值的和y11_y2
y11_y2=0
for i in range(0,len(sales1)):
   y11_y2=y11_y2+(sales1[i]-y2)
print("预测销售值-预测销售平均值的和为:",y11_y2)
#求月销售额y-他的平均值的平方和
Syy=0#y-y1的值的平方和
for i in range(0,len(Y)):
    Syy=Syy+((Y[i]-y1)*(Y[i]-y1))
print("Syy=",Syy)
#求y1-y1平均的平方和
Sy1y1=0
for i in range(0,len(sales1)):
    Sy1y1=Sy1y1+((sales1[i]-y2)*(sales1[i]-y2))
print("Sy1y1=",Sy1y1)
#（y1-y1平均）*（y-y平均）
Syy1=0
for i in range(0,len(sales1)):
    Syy1=Syy1+((Y[i]-y1)*(sales1[i]-y2))
print("Syy1=",Syy1)
#求R
R=Syy1/((Syy*Sy1y1)**0.5)
R2=R*R
print("判定系数R2=",R2)

运行结果

excel分析