The Gradient Descent---梯度下降（Gradient Descent）
文章目录
- 一.什么是梯度？（What’s Gradient）
- 1.分析导数，偏微分，引出梯度的概念
- （1）导数derivative
- （2）偏微分, partial derivative
- （3）梯度, gradient
- 二.梯度的表示（What does Gradient mean?）
- 三.如何使用Gradient去求解（搜索）最小的Loss呢？（How to search?）
- 1.图解梯度----梯度的方向： ∇ f ( θ ) → \nabla f(\theta) \rightarrow ∇f(θ)→larger value
- 2.（寻找损失函数最小值）Search for minima:
- （1）.分析图四
- （2）.梯度下降的再理解：
- a.要求解最小值的损失函数（Loss）：
- b.求解梯度下降的过程及目的
- （3）举例（For instance）
- 四.梯度的几何理解
- 五.学习（训练）的过程图解（Learning Process ）
- 学习（训练）的过程图解一（Learning Process 1）
- 学习（训练）的过程图解二（Learning Process 2）
一.什么是梯度？（What’s Gradient）
DeepLearning的核心就是Gradient
解决什么问题？
用于解决回归问题和神经网络训练过程中的误差问题
在回归和神经网络里边每一个算法都有它的损失函数（误差）
回归算法和神经网络算法知道预测的时候有误差，所以不断地去减少误差，权重不同得到的拟合直线也是不一样的，于是就使用梯度下降的方法一步一步迭代去优化，一步一步迭代去更新。
1.分析导数，偏微分，引出梯度的概念
（1）导数derivative
- 概念：导数就是用来找到“线性近似”的数学工具。
- 核心思路：“以直代曲，线性逼近”（用直线去拟合曲线）
导数概念详解
实际上一个二维的或者三维的函数，它的导数可以沿着任意的方向，例如像下边这个像马鞍一样的函数，它的导数可以沿着任何一个方向。
图一
这里z对x求微分就是求z在x轴的方向上的变动范围，因为是沿着x轴的一个变动，故跟y没有什么关系，得到的偏微分就是变动率（比如这里的-2x, 2y）
（2）偏微分, partial derivative
偏微分是指一个方程中有多个变量，如果我们对其中一个变量求导，假设其他变量看作常数。这样即针对这一个变量的偏导，即偏微分
（3）梯度, gradient
梯度是一个向量。
将沿着所有轴的方向求得的偏微分组成一个向量,这个向量的方向代表这综合的导数的方向，这个向量就叫做梯度。
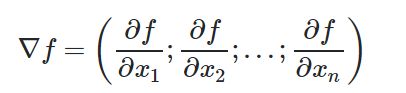
二.梯度的表示（What does Gradient mean?）
图二
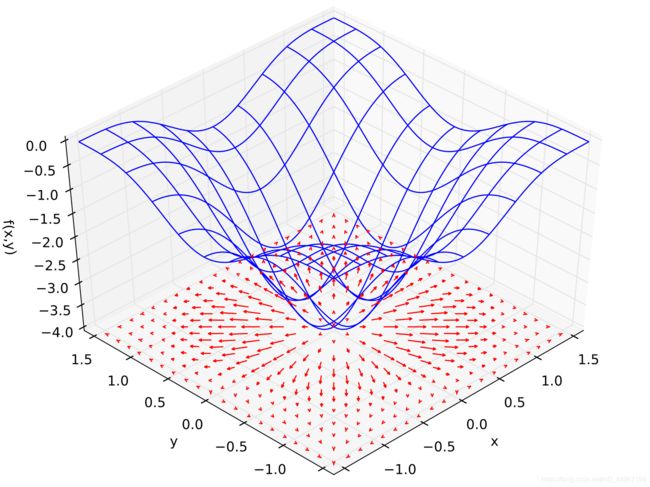
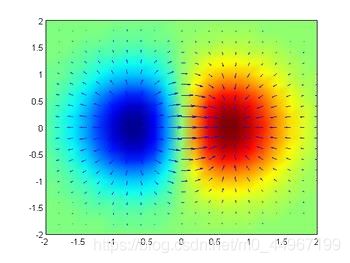
红色箭头的方向就代表着Gradient的方向，红色箭头的长度就代表了当前梯度的模，或者说是当前梯度的长度可以非常直观的看出来，漏斗的最低点就是箭头的源头，在比较陡的地方箭头的长度比较长，梯度的长度比较长到了外围变平坦之后，箭头的长度几乎快要没有了，这里可以直截了当的解释，梯度的方向就代表函数值增大的方向，梯度的模（长度）代表函数增长的速率
图三
上边这个两个球的例子也可以看出，蓝色点代表函数值比较小的值，红色点就代表函数值比较大的值，表示梯度的箭头从小的值开始往外扩散，红色和蓝色相交的部分是增长最快的地方，箭头是最长的。
三.如何使用Gradient去求解（搜索）最小的Loss呢？（How to search?）
这里的Loss 是训练（创造）出来的函数与原函数之间的差值，越小就拟合的越好，也就越有可能收敛，所以要求解它的最小值。
1.图解梯度----梯度的方向： ∇ f ( θ ) → \nabla f(\theta) \rightarrow ∇f(θ)→larger value
Gradient的方向就代表函数值增大的方向 : ∇ f ( θ ) → \nabla f(\theta) \rightarrow ∇f(θ)→larger value
图四
2.（寻找损失函数最小值）Search for minima:
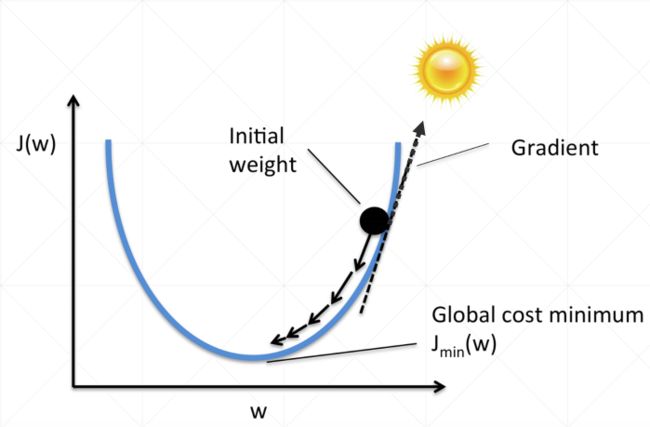
（1）.分析图四
上边图像是损失函数: J ( w ) J(w) J(w)
接下来求解损失函数 J ( w ) J(w) J(w)的最小值
这里设置两个learning rate（学习率/因子）：
l r ： lr： lr： α \alpha α ， η \eta η
θ t + 1 = θ t − α t ∇ f ( θ t ) \theta_{t+1}=\theta_{t}-\alpha_{t} \nabla f\left(\theta_{t}\right) θt+1=θt−αt∇f(θt)
其中， θ t \theta_{t} θt是自变量参数（权重）向量，即当前坐标， α t \alpha_t αt是学习因子，即下山每次前进的一小步（步进长度）， θ t + 1 \theta_{t+1} θt+1是下一步，即下山移动一小步之后的位置。
− α t ∇ f ( θ t ) -\alpha_{t} \nabla f\left(\theta_{t}\right) −αt∇f(θt)表示把当前的参数值按照梯度值相反的方向去更新，因为它总是往损失函数的函数值减少的方向进行的
（2）.梯度下降的再理解：
a.要求解最小值的损失函数（Loss）：
l o s s = ∑ i = 1 n ( h w ( x i ) − y i ) 2 = ∑ i = 1 n ( w T ∗ x i + b − y i ) 2 loss = \sum_{i=1}^{n}(h_w(x_i)-y_i)^2= \sum_{i=1}^{n}(w^T*x_i+b-y_i)^2 loss=i=1∑n(hw(xi)−yi)2=i=1∑n(wT∗xi+b−yi)2
这里的loss function经过求和之后可能会比较大，所以在求和的基础上再求一个平均值可能会更加实用一些
b.求解梯度下降的过程及目的
我们的目的就是要得到一组最好的w′和b′,使得新的x(样本)经过这个模型的输出（w′x+b′)(这里不一定是一阶线性的),能够非常好的接近于这个模型的真实的数值y.
在这里将求解w′和b′，最终转化为求解minimize（loss）
w′和b′每一次更新的依据(求导下降)：
w ′ = w − α ∗ ∂ l o s s ∂ w w' = w - \alpha*\frac{\partial loss}{\partial w} w′=w−α∗∂w∂loss
b ′ = w − α ∗ ∂ l o s s ∂ b b' = w - \alpha*\frac{\partial loss}{\partial b} b′=w−α∗∂b∂loss
α是学习率（learning rate），需要手动指定（也就是超参数）
这里为什么要指定那个学习率（衰减因子，防止步长过大），因为进行梯度下降的时候，每一步步幅可能过大，从而跨过最低点，是用来缩小步长的。 梯度的方向是指向函数值增大的方向，所以每次更新的时候是按照梯度的反方向进行更新的
∂ l o s s ∂ b \frac{\partial loss}{\partial b} ∂b∂loss 表示梯度的方向.
理解：沿着这个函数下降的方向找，最后就能找到山谷的最低点（找到损失函数的最小值），然后 更新W值，这个过程是一个迭代的过程（即沿着梯度下降的方向进行迭代优化）
使用场景：
面对训练数据规模十分庞大的任务
（3）举例（For instance）
求解损失函数最小值的一个过程：
这里上边的Function,就是Cost Function,和下边的Cost Function一样的。
下图中的 h θ ( x ) = θ 0 + θ 1 x h_{\theta}(x)=\theta_{0}+\theta_{1} x hθ(x)=θ0+θ1x就是假设的（创造出来的）
图五
在这里做一个假设：
θ 1 = 4 ； θ 2 = − 4 θ1=4；θ2=-4 θ1=4；θ2=−4
Δ θ 1 = 8 ； Δ θ 2 = − 8 Δθ1=8；Δθ2=-8 Δθ1=8；Δθ2=−8
θ 1 ′ = 4 − 0.01 ∗ 8 θ1′=4-0.01*8 θ1′=4−0.01∗8
θ 2 ′ = − 4 − 0.01 ∗ ( − 8 ) θ2′=-4-0.01*(-8) θ2′=−4−0.01∗(−8)
当 θ > 0 时 ， 会 使 θ 不 断 减 小 当θ>0时，会使θ不断减小 当θ>0时，会使θ不断减小
当 θ < 0 时 ， 会 使 θ 不 断 增 大 当θ<0时，会使θ不断增大 当θ<0时，会使θ不断增大
往 θ 1 ， θ 2 都 为 0 的 全 局 最 小 值 点 靠 近 往θ1，θ2都为0的全局最小值点靠近 往θ1，θ2都为0的全局最小值点靠近
θ1=0；θ2=0
要想通过数值计算达到这个最小值就要一步步的更新，逼近
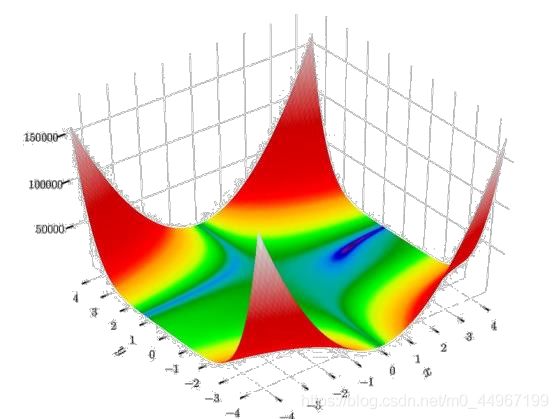
四.梯度的几何理解
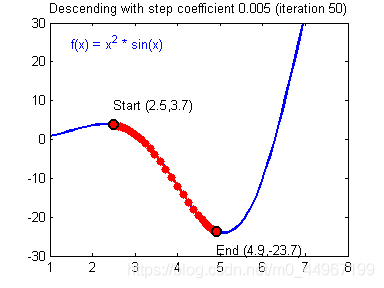
图六
学习（训练）的过程图解二（Learning Process 2）
这里主要表现函数优化收敛的过程（梯度的变化）
图七
图八
图八是图七局部的放大。
图一的动态变化展示.
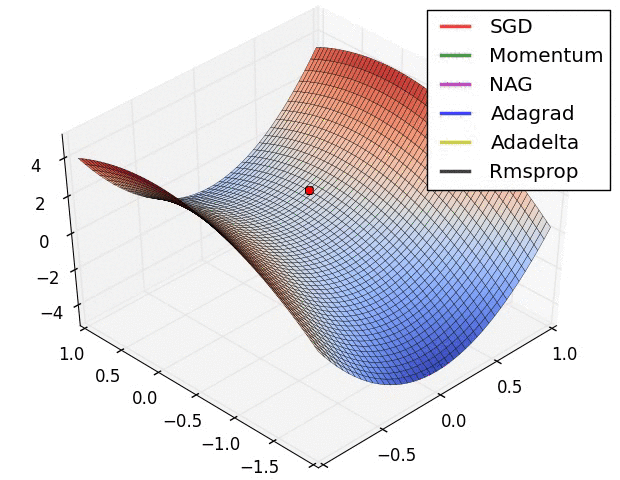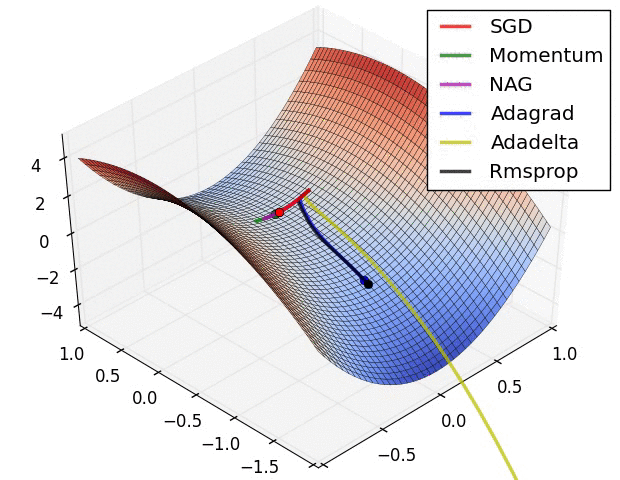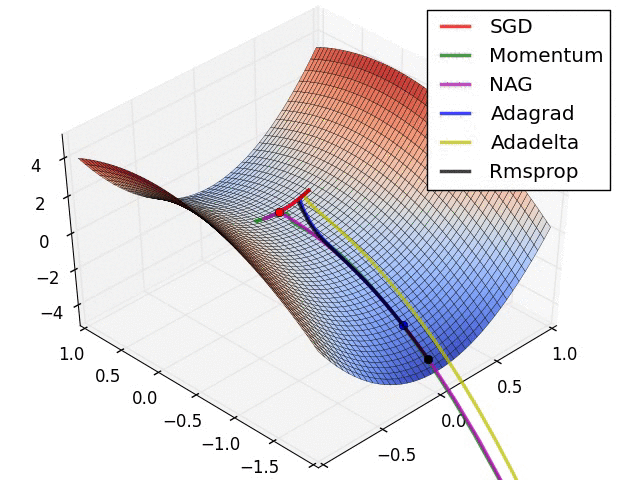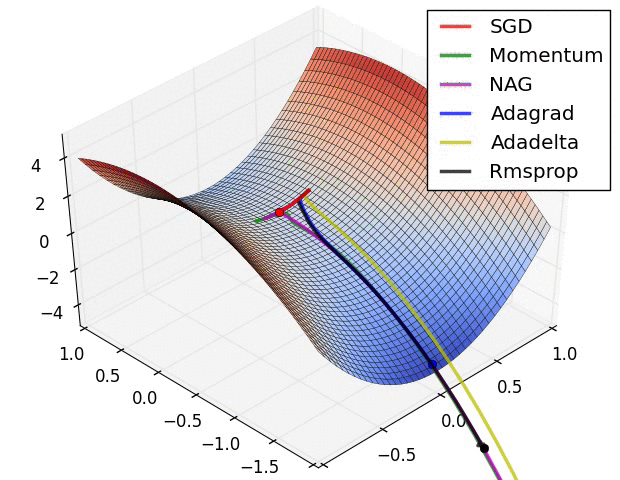
图九
相关梯度知识见有道云笔记：文档：LinearRegression-知识体系.md链接：
梯度下降的代码实现