《Think Python》课后实现合集(更新至 练习4-5)
《Think Python》课后实现合集
- 这是什么?
- 课堂笔记&课后作业
- 第1章 程序之道
- 练习 1-1:在交互模式中故意犯错(1)
- 练习 1-2:解释器牌计算器(时间换算、距离换算、速度换算)
- 第2章 变量、表达式和语句
- 练习 2-1:在交互模式中故意犯错(2)
- 练习 2-2:解释器牌计算器(球体积、书总价、晨练到家时间)
- 第3章 函数
- 练习 3-1:输入长度<70的任意字符串,让其最后一个字母在第70列上
- 练习 3-2:在函数中调用另一个函数
- 练习 3-3:用函数画表格
- 第4章 案例研究:接口设计
- 课堂笔记 Python安装
- 练习 4-1 本章示例代码栈图、停止点偏离思考
- 练习 4-2 用函数画花朵
- 练习 4-3 用函数画雨伞
- 练习 4-4 用函数画大写字母表
- 练习 4-5 用函数画阿基米德螺旋
- 关于《Think Python》课堂笔记&课后作业
- 报错记录
- 更新记录
这是什么?
你好!这里是九月初夏的 《Think Python》作业本 !在这里我将记录自己《Think Python》的章节练习和解题思路,希望能和你一起度过奇妙的编程初见之旅~ 为了便于寻找和我自己区分,我给每个习题都取了个名字。
- 这是《Think Python》哪个版本的作业?
《Think Python:如何像计算机科学家一样思考》第二版(基于Python 3),各大购书平台有售。当然便于写作业的时候“誊抄”题目,我找到了一本双语PDF(作者让这本书基于GNU自由文档许可协议“开源”了,但是该版本部分习题和纸书不同),来自哈尔滨工业大学 车万翔教授 ,渠道是中国大学MOOC。
- 可以当成《Think Python》参考答案吗?
参考答案建议还是以 绿茶出版社官方代码 为准。这里主要存放的还是我的个人答案和解题感悟,当然因为是编程初见,很有可能出现 无法求解 的情况,你有可能看到的是无法正确实现题目要求的代码。当然,如果发生这种情况我会再放一份官方代码研究,并 分析原因、总结规律 ,当然希望这种情况不要发生_(:зゝ∠)_ 还有就是一些没有官方答案的题目,我也不能保证100%正确_(:зゝ∠)_
课堂笔记&课后作业
第1章 程序之道
练习 1-1:在交互模式中故意犯错(1)
【习题 1.1.1】 在 print 语句中,如果漏掉一个括号,或者两个都漏掉,会发生什么?
【求解】
情况1:漏掉左括号,或者都漏掉
>>> print 'Holle, World!')
File "" , line 1
print 'Holle, World!')
^
SyntaxError: Missing parentheses in call to 'print'. Did you mean print('Holle, World!'))?
>>>print 'Holle, World!'
File "" , line 1
print 'Holle, World!')
^
SyntaxError: Missing parentheses in call to 'print'. Did you mean print('Holle, World!'))?
| 序号 | 报错 | 含义 |
|---|---|---|
| 1 | SyntaxError: Missing parentheses in call to ‘print’. | 语法错误:调用时缺少括号 |
推测原因:Python 2 中 print 语句不需要括号,而Python 3 需要,所以这里特别说明缺少括号并给出了可能的建议
情况2:漏掉右括号
>>>print ('Holle, World!'
^
SyntaxError: unexpected EOF while parsing
| 序号 | 报错 | 含义 |
|---|---|---|
| 2 | SyntaxError: unexpected EOF while parsing | 语法错误:解析时意外终止 |
推测原因:解释器从左往右读代码, print 语句没有终止符,后面又没有东西,就“意外终止”了
【习题 1.1.2】 如果正尝试打印一个字符串,那么漏掉一个货所有引号,会发生什么?
【求解】
情况1:漏掉左引号,或者都漏掉
>>>print (Holle, World!')
File "" , line 1
print (Holle, World!')
^
SyntaxError: invalid syntax
>>>print (Holle, World!)
File "" , line 1
print (Holle, World!)
^
SyntaxError: invalid syntax
| 序号 | 报错 | 含义 |
|---|---|---|
| 3 | SyntaxError: invalid syntax | 语法错误:无效语法 |
推测原因:没有引号,解释器将括号里的“Holle, World!”当成了一个变量名,但是逗号、空格、感叹号是非法字符,违背了变量命名的规则,去掉这些符号后,报错就变成了“命名错误:命名没有被定义”了
>>>print ('HolleWorld')
Traceback (most recent call last):
File "" , line 1
print (HolleWorld)
NameError: name 'HolleWorld' is not defined
| 序号 | 报错 | 含义 |
|---|---|---|
| 5 | NameError: name ‘HolleWorld’ is not defined | 命名错误:命名没有被定义 |
情况2:漏掉右引号
>>>print ('Holle, World!)
File "" , line 1
print ('Holle, World!)
^
SyntaxError: EOL while scanning string literal
| 序号 | 报错 | 含义 |
|---|---|---|
| 4 | SyntaxError: EOL while scanning string literal | 语法错误:扫描字符串时行终止 |
推测原因:解释器从左往右读代码,字符串没有终止符,但是print语句却终止了,故“扫描字符串时行终止”
【习题 1.1.3】 可以使用一个负号来表示负数,如-2。如果在数字之前放一个正好,会发生什么?如果是2++2呢?
【求解】
>>> -2
-2
>>> 2++2
4
【习题 1.1.4】 在数学标记里,前置 0 是没有问题的,如 02。在 Python 中也这么做会发生什么?
【求解】
>>> 02
2
【习题 1.1.5】 如果在两个值之间不放任何操作符,会发生什么?
【求解】
情况1:两个值中间无空格:
>>> 24
24
情况2:两个值中间有空格:
>>> 2 4
File "" , line 1
2 4
^
SyntaxError: invalid syntax
| 序号 | 报错 | 含义 |
|---|---|---|
| 3 | SyntaxError: invalid syntax | 语法错误:无效语法 |
练习 1-2:解释器牌计算器(时间换算、距离换算、速度换算)
【习题 1.2.1】 在42分42秒钟,一共有多少秒?
【求解】
>>> 42*60+42
2562
【习题 1.2.2】 10千米相当于多少英里?提示:1英里相当于1.61千米。
【求解】
>>> 10/1.61
6.211180124223602
【习题 1.2.3】 如果你42分42秒跑完10千米,那么你的平均速度(跑1千米需要的分钟和秒数)是多少?平均速度是多少千米每小时?
【求解】
问题1:跑1千米需要的分钟和秒数:
分钟:
>>> (42*60+42)/10/60
4
秒数:
>>> (42*60+42)/10.0%60
16.19999999999999
问题2:平均速度是多少千米每小时:
>>> 10.0/(42*60+42)*60*60
14.051522248243561
第2章 变量、表达式和语句
练习 2-1:在交互模式中故意犯错(2)
【习题 2.1.1】 我们已经见过 n = 42 是合法的。那么 42 = n 呢?
【求解】
>>> 42 = n
File "" , line 1
SyntaxError: can't assign to literal
| 序号 | 报错 | 含义 |
|---|---|---|
| 6 | SyntaxError: can’t assign to literal | 语法错误:不能给文字赋值 |
【习题 2.1.2】 那么 x = y = 1呢?
【求解】
>>> x = y = 1
>>> x
1
>>> y
1
【习题 2.1.3】 有些语言中,每个语句都需要以分好(;)结尾。如果你在 Python 语句的结尾放一个分好,会有什么情况?
【求解】
>> x = y = 1
>>> print(x);print(y)
1
1
【习题 2.1.4】 如果在语句结尾放的是句号呢?
【求解】
>>> print(x).
File "" , line 1
print(x).
^
SyntaxError: invalid syntax
| 序号 | 报错 | 含义 |
|---|---|---|
| 3 | SyntaxError: invalid syntax | 语法错误:无效语法 |
【习题 2.1.5】 在数学标记中,对于 x 乘以 y,可以这么表达:xy。在Python中这样尝试会有什么结果?
【求解】
>>> x = 2
>>> y = 4
>>> xy
Traceback (most recent call last):
File "" , line 1, in <module>
NameError: name 'xy' is not defined
| 序号 | 报错 | 含义 |
|---|---|---|
| 5 | NameError: name ‘HolleWorld’ is not defined | 命名错误:命名没有被定义 |
练习 2-2:解释器牌计算器(球体积、书总价、晨练到家时间)
【习题 2.2.1】 半径为 r r r 的球体的体积是 ( 4 / 3 ) π r 3 (4/3)πr^{3} (4/3)πr3。半径为 5 5 5 的球体体积是多少?
【求解】
>>> (4.0/3)*3.14*5**3
523.3333333333334
【习题 2.2.2】 假设一本书的定价是24.95美元,但是书店打了40%的折扣(6折)。运费是一本3美元,每加一本加75美分。60本书的总价是多少?
【求解】
>>> 24.95*(1-0.4)*60+3+0.75*(60-1)
945.4499999999999
【习题 2.2.3】 如果我 06:52 时离开家,并以慢速(6分10秒/千米)跑1.6千米,接下来以4分30秒/千米的速度跑4.8千米,再以慢速跑1.6千米。请问我回家吃早餐时什么时候?
【求解】
时:
>> 6+1
7
分:
>>> (52+((6*60+10)*1.6*2+(4*60+30)*4.8-((6*60+10)*1.6*2+(4*60+30)*4.8)%60)/60)%60
33.0
秒:
>>> 0+((6*60+10)*1.6*2+(4*60+30)*4.8)%60
20.0
第3章 函数
练习 3-1:输入长度<70的任意字符串,让其最后一个字母在第70列上
【习题 3.1.1】 编写一个函数 right_justify,接收一个字符串形参 s,并打印出足够的前导空白,以达到最后一个字符显示在第70列上。
>>> right_justify('monty')
monty
提示:可以利用字符串的拼接和重复特性。另外,Python提供了一个内置名为 len 的函数,返回一个字符串的长度,所以 len(‘allen’) 的值是5。
【求解】
先计算s的长度l,前导空白=空格*(70-l):
>>> def right_justify(s):
... l = len(s)
... print(' '*(70-l)+s)
...
>>> right_justify('monty')
monty
将len(s)带入l,还能更剪短点:
>>> def right_justify(s):
... print(' '*(70-len(s))+s)
...
>>> right_justify('monty')
monty
练习 3-2:在函数中调用另一个函数
函数对象是一个值,可以将它赋值给变量,或者作为实参传递。例如,do_twice 是一个函数,接收一个函数对象作为实参,并调用它两次:
def do_twice(f):
f()
f()
下面是一个使用 do_twice 来调用一个 print_spam 函数两次的示例:
def print_spam():
print('spam')
do_twice(print_spam)
【习题 3.2.1】 将这个示例存入脚本并测试它。
【求解】
代码:
def do_twice(f):
f()
f()
def print_spam():
print('spam')
do_twice(print_spam)
运行结果:
spam
spam
【习题 3.2.2】 修改 do_twice,让他接收两个实参,一个是函数对象,另一个是一个值,它会调用函数对象两次,并传入那个值作为实参。
【求解】 这让我想起了代数 y=g(f(x),x)
代码:
def do_twice(f,x):
f(x)
f(x)
def print_spam(x):
print(x)
do_twice(print_spam,'spam')
运行结果:
spam
spam
【习题 3.2.3】 将本章前面介绍的函数 print_twice 的定义复制到你的脚本中。
【求解】
def print_twice(bruce):
print(bruce)
print(bruce)
【习题 3.2.4】 使用修改版的 do_twice 来调用 print_twice 两次,并传入实参 ‘spam’。
【求解】
代码:
def do_twice(f,x):
f(x)
f(x)
def print_twice(bruce):
print(bruce)
print(bruce)
do_twice(print_twice,'spam')
运行结果:
spam
spam
spam
spam
【习题 3.2.4】 定义一个新的函数 do_four,接收一个函数对象与一个值,使用这个值作为实参调用函数4次。这个函数的函数体应该只有2条语句,而不是4条。
【求解】 在 do_four 里调用 do_twice 两次,从而实现调用实参函数4次(2×2)
代码:
#执行函数f(x)两次
def do_twice(f,x):
f(x)
f(x)
#通过执行do_twice(f,x)两次,实现执行f(x)四次
def do_four(f,x):
do_twice(f,x)
do_twice(f,x)
#定义最终被调用的函数
def print_spam(x):
print(x)
#执行将'spam'打印四次
do_four(print_spam,'spam')
执行结果:
spam
spam
spam
spam
练习 3-3:用函数画表格
注意:这个练习应该仅使用当前我们学过的语句和特性来实现。
【习题 3.3.1】 编写一个函数,绘制如下表格:
![]()
提示:要在同一行打印出个值,可以使用逗号分隔不同的值:
print ('+', '-')
如果一个序列以逗号结尾,Python会认为这一行没有结束, 于是下一个打印出的值会
出现在同一行。
print ('+', end=' ')
print ('-')
这两条语句的输出结果是’+ -’。
一条单独的print语句会结束当前行,开始下一行。
【分析】
第一步:先分析表格下表格![]()
第二布:确认下方案
首先,题目给出的 print 语句的用法肯定是有用的
print ('+', end=' ')
print ('-')
其次,【习题 3.2.4】 的 do_twice 和 do_four 也是有用的
#执行函数f(x)两次
def do_twice(f,x):
f(x)
f(x)
#通过执行do_twice(f,x)两次,实现执行f(x)四次
def do_four(f,x):
do_twice(f,x)
do_twice(f,x)
所以我打算用 do_twice 画边界和空白的每一条,再用 do_four 画4条空白的行高
【求解】
#执行函数f(x)两次
def do_twice(f,x,y):
f(x,y)
f(x,y)
#通过执行do_twice(f,x)两次,实现执行f(x)四次
def do_four(f,x,y):
do_twice(f,x,y)
do_twice(f,x,y)
#画出表格的每条,边界、空白可用
def do(x,y):
print (x, end=' ')
print (x, end=' ')
print (y)
#画出表格的“一行”:1条上边+4条行高
def line():
do('+ - - - -','+')
do_four(do,'| ','|')
#画出表格:2行+1底边
def list():
line()
line()
do('+ - - - -','+')
list()
【再解】 瞄了一眼,下面 【习题 3.3.1】 要求变成 4 × 4 的表格,我想能不能把变量尽量提出来,改变表格的时候改个数字就好了?最后发现列很容易做到(用《Think Python》13页《2.6 字符串操作》中的 ‘Spam’*3),行还是要靠 print 语句一行一行打印。
当然此方法中的“+ - - - - ”和“| ”要比 【求解】 中多1个空格
#变量:表格列数
n = 2
#n列表格的1条:n个循环体+1个终止符,边界、空白均可使用
def cell(x,y,n):
print(x*n+y)
#行高:4条空白(直接4条,懒得再定义do_twice和do_four了)
def line_height_4(n):
cell('| ','|',n)
cell('| ','|',n)
cell('| ','|',n)
cell('| ','|',n)
#行:一条边界+行高
def line(n):
cell('+ - - - - ','+',n)
line_height_4(n)
#表格:2行+1底
def list(n):
line(n)
line(n)
cell('+ - - - - ','+',n)
#执行表格函数,打印出表格
list(n)
【习题 3.3.2】 编写一个函数绘制类似的表格,单有4行4列。
【求解】 基于 【习题 3.3.1】 中的 【求解】,用了 do_twice 和 do_four,没有被拿出来的变量。
代码变动:需要在画“每条”时多打印“列” print (x, end=’ ') 2次,画表格的时候多打印“行” line() 2次
#执行函数f(x)两次
def do_twice(f,x,y):
f(x,y)
f(x,y)
#通过执行do_twice(f,x)两次,实现执行f(x)四次
def do_four(f,x,y):
do_twice(f,x,y)
do_twice(f,x,y)
#画出表格的每条,边界、空白可用
def do(x,y):
print (x, end=' ')
print (x, end=' ')
print (x, end=' ')
print (x, end=' ')
print (y)
#画出表格的“一行”:1条上边+4条行高
def line():
do('+ - - - -','+')
do_four(do,'| ','|')
#画出表格:2行+1底边
def list():
line()
line()
line()
line()
do('+ - - - -','+')
list()
【再解】 基于 【习题 3.3.1】 中的 【再解】,没有使用 do_twice 和 do_four,变量 n 派上了用场!
代码变动:将 n 的值从 2 改成 4,最后画表格的时候多打印“行” line(n) 2次
#变量:表格列数
n = 4
#n列表格的1条:n个循环体+1个终止符,边界、空白均可使用
def cell(x,y,n):
print(x*n+y)
#行高:4条空白(直接4条,懒得再定义do_twice和do_four了)
def line_height_4(n):
cell('| ','|',n)
cell('| ','|',n)
cell('| ','|',n)
cell('| ','|',n)
#行:一条边界+行高
def line(n):
cell('+ - - - - ','+',n)
line_height_4(n)
#表格:2行+1底
def list(n):
line(n)
line(n)
line(n)
line(n)
cell('+ - - - - ','+',n)
#执行表格函数,打印出表格
list(n)
第4章 案例研究:接口设计
课堂笔记 Python安装
在第4章之前,作者鼓励读者在 PythonAnywhere 上测试和联系,当然由于众所知周的原因根本打不开,不过我找到了个很好用的国内版《菜鸟工具》,我到本章目前为止的测试和练习都是在菜鸟上面完成的。
进入本章后,由于要使用 tutle 模块,作者说 PythonAnywhere 上用不了 turtle 模块(当然菜鸟工具上也不行),所以“现在正是安装 Python 的好时机”,然而这个“好时机”的教学短连接 失效了 ……
不过好在还有伟大的 Python.org:
在 Dowdload 里直接下载最新版本,像安装游戏一样就安好了(windows和mac都是一样的简单!):
然后在 About - Help 里面正好找到一篇《Python for Non-Programmers》拉到最底下 Tools 介绍了一个适合初学者的轻量级的 Python IDE Thonny(当然由于众所周知的原因下载也很慢,我是用迅雷慢慢下下来的),Thonny 也像游戏一样很好安装,安好后就可以跑第4章的内容啦~
至于我是怎么知道 IDE 是啥玩意儿还是要感谢车万翔老师在中国大学MOOC上的Python课……但是由于基于Python 2,而且还是2015年的课了(而且还停课了),我就弃了……不过由于《Think Python》是该课的指定教材,我就开始自学《Think Python》啦~(到目前为止还没有受挫,希望能安稳啃完)。
练习 4-1 本章示例代码栈图、停止点偏离思考
【习题 4.1.1】 画一个栈图来显示函数 circle(bob, radius) 运行时的程序状态。
《Think Python》第4章示例代码(仅circle相关,完整版点击):
"""This module contains a code example related to
Think Python, 2nd Edition
by Allen Downey
http://thinkpython2.com
Copyright 2015 Allen Downey
License: http://creativecommons.org/licenses/by/4.0/
"""
from __future__ import print_function, division
import math
import turtle
def polyline(t, n, length, angle):
"""Draws n line segments.
t: Turtle object
n: number of line segments
length: length of each segment
angle: degrees between segments
"""
for i in range(n):
t.fd(length)
t.lt(angle)
def arc(t, r, angle):
"""Draws an arc with the given radius and angle.
t: Turtle
r: radius
angle: angle subtended by the arc, in degrees
"""
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
# making a slight left turn before starting reduces
# the error caused by the linear approximation of the arc
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
def circle(t, r):
"""Draws a circle with the given radius.
t: Turtle
r: radius
"""
arc(t, r, 360)
# the following condition checks whether we are
# running as a script, in which case run the test code,
# or being imported, in which case don't.
if __name__ == '__main__':
bob = turtle.Turtle()
# draw a circle centered on the origin
radius = 100
bob.pu()
bob.fd(radius)
bob.lt(90)
bob.pd()
circle(bob, radius)
# wait for the user to close the window
turtle.mainloop()
【求解】 在加入 print 语句之后,发现 bob 的值是
| 所属函数 | 变量 |
|---|---|
| __ main__ | bob ——> |
| __ main__ | radios ——> 100 |
| circle | t ——> |
| circle | r ——> 100 |
| arc | t ——> |
| arc | r ——> 100 |
| arc | angle ——> 360 |
| polyline | t ——> |
| polyline | n ——> 160 |
| polyline | length ——> 3.9269908169872414 |
| polyline | angle ——> 2.25 |
因为 CSDN 的 Markdown 文字两侧连打2个下划线是加粗,所以main的前面多了个空格(强迫症勿怪)
【习题 4.1.2】 在 4.7 节中的 arc 函数并不准确,因为使用多边形模拟近似圆,总是会在真实的圆之外。因此,Turtle 画完线之后会停在偏离正确的目标几个像素的地方。我的解决方案里展示了一种方法可以减少这种错误的效果。阅读代码并考虑是否合理。如果你自己画图,可能会发现它是如何生效的。
【求解】 先对比代码有何不同
《4.7 节》的 arc 函数:
def arc(t, r, angle):
arc_length = 2 * math.pi * r * angle / 360
n = int(arc_length / 3) + 1
step_length = arc_length / n
step_angle = angle / n
for i in range(n):
t.fd(step_length)
t.lt(step_angle)
《练习 4-1》的arc 函数:
def polyline(t, n, length, angle):
"""Draws n line segments.
t: Turtle object
n: number of line segments
length: length of each segment
angle: degrees between segments
"""
for i in range(n):
t.fd(length)
t.lt(angle)
def arc(t, r, angle):
"""Draws an arc with the given radius and angle.
t: Turtle
r: radius
angle: angle subtended by the arc, in degrees
"""
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
# making a slight left turn before starting reduces
# the error caused by the linear approximation of the arc
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
《练习 4-1》示例代码给出的解决方案是“在画圆前轻微左偏”,理由是“错误是由弧的线性相似导致的”。
关于 弧的线性相似误差 :
《Think Python》又名《重拾三角函数》。
由于本人脱离学校太久,总之根据本人已经没法证明的三角函数求极限理论,当近似圆中每个小三角夹角足够小的时候,近似圆就越接近圆,真实的圆并不完全在近似圆之内或之外,真实圆的弧不停的跨过近似圆的边,像这样:

这种近似圆与真实圆的误差会导致多边形的角在真实圆之外,即每当开始或停止画直线的时候,乌龟会停在多边形的角上,即真实圆之外。
关于处理方案:
#左转半个step_angle
t.lt(step_angle/2)
#画一个近似圆
for i in range(n):
t.fd(length)
t.lt(angle)
#右转半个step_angle
t.rt(step_angle/2)
我将 arc 函数引用的 polyline 函数中的 for 循环展开了,可以先看出来处理方案的 arc 函数是先左转半个 step_angle 的角度,再画一个 完整的 近似圆,画完后再讲乌龟右转半个 step_angle 归位:

老实说我并不觉得这种 “再画圈前稍微左转一点点(making a slight left turn before starting reduces)”的骚操作除了让画出的近似圆比之前的右偏半个 step_angle 对于画出的多边形本身并没有任何影响,为何作者会认为这种操作减小了误差呢?虽然作者说了“如果你自己画图,可能会发现它是如何生效的”,但是我画了更理解不了……
我打算写完第四章作业后,发个帖子找人问问,如果有大佬指点的话,会更新在这里。
我回来了……
在做【练习 4-4:字母表】时发现,如果删除掉
#左转半个step_angle
t.lt(step_angle/2)
#右转半个step_angle
t.rt(step_angle/2)
仅保留
#画一个近似圆
for i in range(n):
t.fd(length)
t.lt(angle)
当你在画J的时候,如果先画一竖,再左移直径画一个半圆,你会发现,根本接不上……
代码:
#引入数学模块、乌龟模块
import math
import turtle
#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
#弧
def arc(t, r, angle):
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
#t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
#t.rt(step_angle/2)
#线段
def line(t, l):
t.fd(l)
#test:J
def draw_j(t, l):
t.rt(90)
line(t, l)
t.pu()
t.rt(90)
line(t, l/2)
t.lt(90)
t.pd()
arc(t, l/4, 180)
draw_j(bob,200)
turtle.mainloop()
效果:
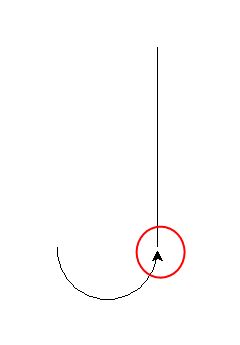
说明 t.lt(step_angle/2) 转的微小角度才是正确的,不转所画的弧线虽然尺寸没问题,但是位置以起点为中心左偏了 t.lt(step_angle/2) 角度。
加上这两行代码(解除注释)后:
#弧
def arc(t, r, angle):
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
效果:
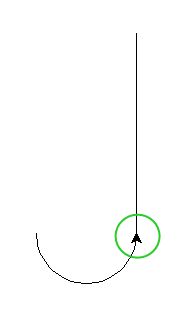
仔细想了下函数 arc(t, r, angle) 的画法,如果开头不左转 t.lt(step_angle/2) 的话,相直线向下画第1笔,再开始“转一个小角度 - 再画一笔”的循环:

这就造成了一个问题:终点没有跟起点水平(没有 t.lt(step_angle/2) 的终点是红色,有 t.lt(step_angle/2) 的终点是绿色),造成了这种效果:

仔细想了一下,数学原因是:由于我们是用很短的直线模拟的曲线,起点和终点的切线斜度就是第一根线和最后一根线的斜度,第一根直线的斜度是0、最后一根切线的斜度是 cot(step_angle),没办法像真正的弧线一样做到起点和终点的切线斜度相同,故需要匀一下,让起点多 step_angle/2,终点少 step_angle/2。
练习 4-2 用函数画花朵
写一组合适的通用函数,用来画出下图所示的花朵图案(最终代码执行效果图):
![]()
【求解】
Step.1 确认组件
如果想通过本张介绍的多边线 polyline(t, n, length, angle) 和弧函数 arc(t, r, angle) 画出花瓣的弧,需要知道:花瓣的弧度和弧长
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
#弧
def arc(t, r, angle):
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
Step.2 抽象问题
已知:花瓣瓣数 n n n,花瓣长度 l l l
求:花瓣的弧度和弧长( polyline(t, n, length, angle) 中的 angle 和 length)
Step.3 问题求解
观察花朵:对于花瓣 不重叠 的花朵,花瓣越多,花瓣越细
故,设:组成花瓣的弧线的弧度(angle)为 2 π n \frac{2π}{n} n2π,以实现“花瓣越多,花瓣越细”的效果
由于在弧度单位下 l = ∣ α ∣ r l=|α| r l=∣α∣r,故还需要知道花瓣弧半径 r r r 才能计算弧长(length)
![]()
由上图求 r r r:
r = l 2 s i n π n r=\frac{l}{2sin\frac{π}{n}} r=2sinnπl
由公式 l = ∣ α ∣ r l=|α| r l=∣α∣r,求弧长length:
l e n g t h = π l n s i n π n length=\frac{πl}{nsin\frac{π}{n}} length=nsinnππl
此时通过 arc(t, r, angle) 可以画出花瓣的一条弧,还需要要转一个角度再画出同样的一条弧,这个角度是花瓣尖角,两条弧相交点的切线夹角,由于花瓣尖角里外相同,每个花瓣尖角也相同,故这个花瓣尖角是根据花瓣数量平分 360 ° 360° 360°: 360 ° n \frac{360°}{n} n360°,转角是花瓣尖角的补角 180 ° − 360 ° n 180°-\frac{360°}{n} 180°−n360°![]()
同时上一个花瓣终点的切线和下一个花瓣起点的切线重合,画完上一个花瓣后,需要转向 180 ° 180° 180° 继续画下一个花瓣:
"""
《Think Python》练习 4-2:用函数画花朵
l:花瓣的长度(花朵的直径)
m:花瓣的个数
"""
#引入数学模块、乌龟模块
import math
import turtle
#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
#弧
def arc(t, angle, arc_length):
#计算:弧分几段画,每段多长,每段之间的夹角
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
#画出弧
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
#不重叠花瓣的花朵
def flower(l,m):
#计算:弧度、弧半径、弧长
arc_angle = 2 * math.pi / m
arc_angle2 = 360 / m
arc_r = l / 2 / math.sin(arc_angle/2)
arc_length = arc_angle * arc_r
#计算:花瓣尖转角度数
angel = 180 - 360.0/m
#画出花朵
for i in range(m):
arc(bob, arc_angle2, arc_length)
bob.lt(angel)
arc(bob, arc_angle2, arc_length)
bob.lt(180)
注意:计算三角弧度单位是弧度(arc_angle = 2 * math.pi / m),乌龟转向单位是度数(arc_angle2 = 360 / m)
对于 花瓣重叠 的花朵,如果其花瓣是 2 n 2n 2n,实际上是画一个花瓣为 n n n 且不重叠的花朵,转半个花瓣尖转角度数(angel = 180 - 360.0/m)再画一朵完全一样的花朵:
至于我为什么知道?完全因为小时候看《百变小樱》的时候,给自己画了个“魔法阵”,就是上图?
#重叠花瓣的花朵
def flower2(l,n):
m = int(n/2)
flower(l,m)
bob.lt(180/m)
flower(l,m)
bob.rt(180/m)
Step.4 完成代码
"""
《Think Python》练习 4-2:通用函数画花朵
l:花瓣的长度(花朵的直径)
m:花瓣的个数
"""
#引入数学模块、乌龟模块
import math
import turtle
#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
#弧
def arc(t, angle, arc_length):
#计算:弧分几段画,每段多长,每段之间的夹角
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
#画出弧
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
#不重叠花瓣的花朵
def flower(l,m):
#计算:弧度、弧半径、弧长
arc_angle = 2 * math.pi / m
arc_angle2 = 360 / m
arc_r = l / 2 / math.sin(arc_angle/2)
arc_length = arc_angle * arc_r
#计算:花瓣尖转角度数
angel = 180 - 360.0/m
#画出花朵
for i in range(m):
arc(bob, arc_angle2, arc_length)
bob.lt(angel)
arc(bob, arc_angle2, arc_length)
bob.lt(180)
#重叠花瓣的花朵
def flower2(l,n):
m = int(n/2)
flower(l,m)
bob.lt(180/m)
flower(l,m)
bob.rt(180/m)
#左移240,画出不重叠花瓣的7瓣花
bob.pu()
bob.fd(-240)
bob.pd()
flower(100,7)
#右移240,画出重叠花瓣的10瓣花
bob.pu()
bob.fd(240)
bob.pd()
flower2(100,10)
#左移240,画出不重叠花瓣的20瓣花
bob.pu()
bob.fd(240)
bob.pd()
flower(100,20)
#下移120,让turtle不遮挡花朵
bob.pu()
bob.rt(90)
bob.fd(120)
turtle.mainloop()
练习 4-3 用函数画雨伞
写一组合适的通用函数,用来画出下图所示的图形(最终代码执行效果图):
![]()
【求解】
不得不说,练习 4-3 比 练习 4-2 简单多了!!!
Step.1 确认组件
由 n n n 个等腰三角形组成“雨伞”
Step.2 抽象问题
已知:雨伞边数 n n n、雨伞边长 l l l
求:等腰三角形顶角、底角
Step.3 问题求解
n n n 个顶角平分 360 ° 360° 360°: 2 π n = 360 n \frac{2π}{n}=\frac{360}{n} n2π=n360
已知等腰三角形顶角 360 n \frac{360}{n} n360,求底角: 180 − 360 n 2 \frac{180-\frac{360}{n}}{2} 2180−n360
已知等腰三角形底边 l l l,求腰长: r = l 2 s i n π n r=\frac{l}{2sin\frac{π}{n}} r=2sinnπl
Step.4 完成代码
"""
《Think Python》练习 4-3:通用函数画雨伞
n:雨伞的边数
l:雨伞的边长
"""
#引入数学模块、乌龟模块
import math
import turtle
#调用乌龟画图
bob = turtle.Turtle()
#雨伞
def umbrella(n,l):
#计算雨伞中每个等边三角形的顶角(angle_in)、底角(angle_out)、腰长(r)
angle_in = 360 / n
angle_out = (180 - angle_in) / 2
r = l / 2 / math.sin(angle_in / 2 / 180 * math.pi)
#重复画等腰三角形完成雨伞
for i in range(n):
bob.lt(angle_in/2)
bob.fd(r)
bob.lt(180 - angle_out)
bob.fd(l)
bob.lt(180 - angle_out)
bob.fd(r)
bob.lt(180 - angle_in/2)
#左移240,画出5瓣雨伞
bob.pu()
bob.fd(-240)
bob.pd()
umbrella(5,115)
#右移240,画出6瓣雨伞
bob.pu()
bob.fd(240)
bob.pd()
umbrella(6,98)
#右移240,画出7瓣雨伞
bob.pu()
bob.fd(240)
bob.pd()
umbrella(7,85)
#下移120,让turtle不遮挡雨伞
bob.pu()
bob.rt(90)
bob.fd(120)
turtle.mainloop()
练习 4-4 用函数画大写字母表
字母表中的字母可以使用一些基本元素来构成,如横线、竖线以及一些曲线。设计一个字母表,可以使用最少的基本元素画出来,并且编写函数来画出字母。

【求解】
这道题教会我最重要的一件事是:用完东西要放回原处。
虽然这么简单的一个道理,父母从小就教,但是我根本没care,常用的东西放在显眼的地方,不常用的东西就随缘了,到用的时候再找。
平时生活中用东西我都当成了一个件独立的事,并没有连成整体思考,但是通过本题 打字机代码 验证的时候把26个字母连成了整体,我第一次验证的时候,虽然能打出字,但是不仅对不齐,甚至有的字母还是躺着的……就是因为画完每个字母乌龟没有归位,后面又花了时间重新给每个字母乌龟用前移动到起点、用完归位。

第二个道理是:将应用模块与公共调用模块彻底分开。
由于验证的时候发生了“没有归位”的问题,当时就想赶紧归位解决了,在每个字母的函数后面直接添加归位位移,结果在验证有的字母就直接变形了。
比如我的G、O、Q是在画完没有归位的C的基础上直接添加直角、竖线、斜线完成的,G、O直接调的C,Q直接调的O,当我给C的乌龟归位后,调用C的这3个字母的其他部分全都跟着位移了……导致后面很多字母都重写了(不仅这几个字母,还有很多直线我之前直接用的draw_i)。
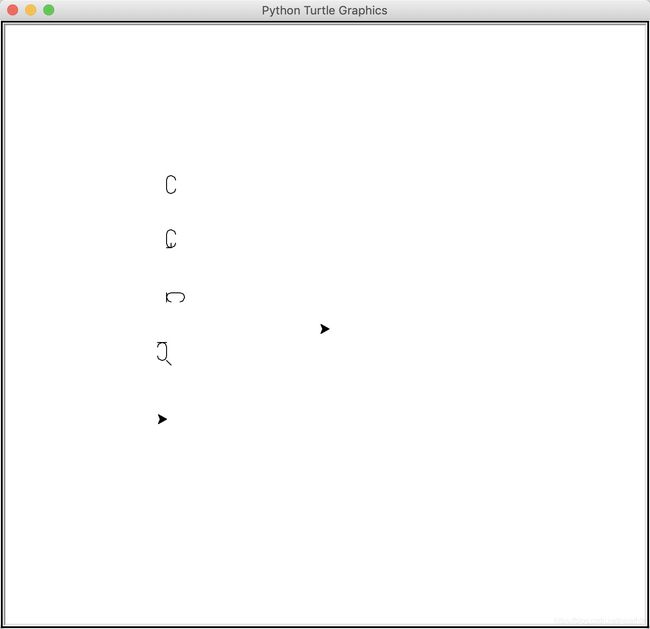
Step.1 设计字体
本来想设计一个像电子表数字的字体,丑点就丑点不要画弧线(弧线麻烦),但是发现26个字母,形态还是挺丰富的,光靠直线不行必须要弧线……
话说这题其实是锻炼抽象能力吧?草稿改了两次,终于统一到只保留横线、竖线、左斜线、右斜线、弧线:
这里N写错了不要在意,后面调试的时候发现改过来了(虽然是在写这篇文章的时候)

Step.2 分类抽象
横竖线:E、F、H、I、L、T
左右斜线:A、K、M、N、V、W、X、Y、Z
半圆+横线:B、P、R
半圆+竖线:J、U
基于C:C、G、O、Q
只有弧线:S
Step.3 问题求解
只有弧线:S
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
#弧
def arc(t, r, angle):
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
横竖线:E、F、H、I、L、T
#线段
def line(t, l):
t.fd(l)
#左转直角
def right_angle(t, l1, l2):
line(t, l1)
t.lt(90)
line(t, l2)
左右斜线:A、K、M、N、V、W、X、Y、Z
#左斜线
def l_slash(t, tan, l):
angle = math.atan(tan) * 180 / math.pi
m = math.sqrt( 1 / tan**2 + 1) * l
t.lt(angle)
line(t, m)
t.rt(angle)
#右斜线
def r_slash(t, tan, l):
angle = math.atan(tan) * 180 / math.pi
m = math.sqrt( 1 / tan**2 + 1) * l
t.rt(angle)
line(t, m)
t.lt(angle)
半圆+横线:B、P、R
#B、P、R公共部分:
def bpr(t, l):
r = l/4
angle = 180
line(t, r)
arc(t, r, angle)
line(t, r)
基于C:C、G、O、Q
#C、G、O、Q公共部分:
def cgoq(t, l):
#移动到起点
t.pu()
right_angle(t, l*1/2, l*3/4)
t.pd()
#C
arc(t, l/4, 180)
line(t, l/2)
arc(t, l/4, 180)
Step.4 完成代码
文件 letters.py 中不要有具体函数的调用指令,要不然你还没打字,typewriter.py 就直接执行这个函数了。也不要有 turtle.mainloop() 指令,要不然还没开始就什么都执行不了。
"""
《Think Python》练习 4-4:字母表
基本元素:弧线、直线、左斜线、右斜线
"""
#引入数学模块、乌龟模块
import math
import turtle
#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
#弧
def arc(t, r, angle):
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
#线段
def line(t, l):
t.fd(l)
#左转直角
def right_angle(t, l1, l2):
line(t, l1)
t.lt(90)
line(t, l2)
#左斜线
def l_slash(t, tan, l):
angle = math.atan(tan) * 180 / math.pi
m = math.sqrt( 1 / tan**2 + 1) * l
t.lt(angle)
line(t, m)
t.rt(angle)
#右斜线
def r_slash(t, tan, l):
angle = math.atan(tan) * 180 / math.pi
m = math.sqrt( 1 / tan**2 + 1) * l
t.rt(angle)
line(t, m)
t.lt(angle)
#B、P、R公共部分:
def bpr(t, l):
r = l/4
angle = 180
line(t, r)
arc(t, r, angle)
line(t, r)
#C、G、O、Q公共部分:
def cgoq(t, l):
#移动到起点
t.pu()
right_angle(t, l*1/2, l*3/4)
t.pd()
#C
arc(t, l/4, 180)
line(t, l/2)
arc(t, l/4, 180)
#A
def draw_a(t, l):
l_slash(t, 4, l)
r_slash(t, 4, l)
#A中的横线
t.pu()
t.lt(90)
right_angle(t, l/2, l*3/8)
t.lt(180)
t.pd()
line(t, l/4)
#归位
t.pu()
t.lt(180)
right_angle(t, l*3/8, l/2)
t.lt(90)
#B
def draw_b(t, l):
bpr(t, l)
t.lt(180)
bpr(t, l)
t.lt(90)
line(t, l)
#归位
t.lt(90)
#C
def draw_c(t, l):
#画C
cgoq(t,l)
#归位
t.pu()
t.lt(90)
right_angle(t, l*1/2, l*1/4)
t.lt(90)
#D
def draw_d(t,l):
arc(t, l/2, 180)
t.lt(90)
line(t, l)
#归位
t.lt(90)
#E
def draw_e(t, l):
#F
draw_f(t, l)
#线
line(t, l/2)
#归位
t.pu()
t.lt(180)
line(t, l/2)
t.lt(180)
#F
def draw_f(t, l):
#移动到起点
t.pu()
right_angle(t, l/2, l)
t.pd()
#直角
t.lt(90)
right_angle(t, l/2, l/2)
#线
t.lt(90)
line(t, l/4)
#直角
t.lt(180)
right_angle(t, l/4, l/2)
#归位
t.lt(90)
#G
def draw_g(t, l):
#画C
cgoq(t, l)
#补G
right_angle(t, l/4, l/4)
#归位
t.pu()
right_angle(t, l/4, l/2)
t.lt(90)
#H
def draw_h(t, l):
t.lt(90)
line(t, l)
t.pu()
t.rt(90)
line(t, l/2)
t.rt(90)
t.pd()
line(t, l)
t.lt(180)
right_angle(t, l/2, l/2)
#归位
t.pu()
t.lt(90)
line(t, l/2)
t.lt(90)
#I
def draw_i(t, l):
#移动到起点
t.pu()
line(t, l/4)
t.lt(90)
#画I
t.pd()
line(t, l)
#归位
t.pu()
t.lt(90)
right_angle(t, l/4, l)
t.lt(90)
#J
def draw_j(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l/4)
t.lt(180)
#画J
t.pd()
arc(t, l/4, 180)
line(t, l*3/4)
#归位
t.pu()
t.lt(90)
right_angle(t, l/2, l)
t.lt(90)
#K
def draw_k(t, l):
#计算斜边长度
m = l * math.sqrt(2) / 2
#画K
t.lt(90)
line(t, l)
t.pu()
t.rt(90)
line(t, l/2)
t.rt(135)
t.pd()
right_angle(t, m, m)
#归位
t.pu()
t.rt(135)
line(t, l/2)
t.lt(180)
#L
def draw_l(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.lt(180)
#画L
t.pd()
right_angle(t, l, l/2)
#归位
t.pu()
t.lt(180)
line(t, l/2)
t.lt(180)
#M
def draw_m(t, l):
t.lt(90)
line(t, l)
t.rt(90)
r_slash(t, 2, l/2)
l_slash(t, 2, l/2)
t.rt(90)
line(t, l)
#归位
t.pu()
t.rt(90)
line(t, l/2)
t.lt(180)
#N
def draw_n(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.lt(180)
#画N
t.pd()
line(t, l)
t.lt(90)
l_slash(t, 2, l)
t.rt(90)
line(t, l)
#归位
t.pu()
t.rt(90)
line(t, l/2)
t.lt(180)
#O
def draw_o(t, l):
cgoq(t, l)
line(t, l/2)
#归位
t.pu()
t.lt(90)
right_angle(t, l/2, l*3/4)
t.lt(90)
#P
def draw_p(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l/2)
t.rt(90)
#画P
t.pd()
bpr(t, l)
t.lt(90)
line(t, l)
#归位
t.lt(90)
#Q
def draw_q(t, l):
#画O
cgoq(t, l)
line(t, l/2)
#画丶
t.pu()
t.lt(90)
right_angle(t, l/4, l/2)
t.lt(90)
t.pd()
r_slash(t, 1, l/4)
#归位
t.pu()
t.lt(180)
line(t, l/2)
t.lt(180)
#R
def draw_r(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l/2)
t.rt(90)
#画P
t.pd()
bpr(t, l)
t.lt(90)
line(t, l)
#画丶
t.lt(180)
line(t, l/2)
t.rt(90)
r_slash(t, 1, l/2)
#归位
t.pu()
t.lt(180)
line(t, l/2)
t.lt(180)
#S
def draw_s(t, l):
#移动到起点
t.pu()
right_angle(t, l/2, l*3/4)
#画270°弧
t.pd()
arc(t, l/4, 270)
t.pu()
t.lt(180)
right_angle(t, l/4, l/4)
t.pd()
arc(t, l/4, 270)
#归位
t.pu()
right_angle(t, l/4, l/2)
t.lt(90)
#T
def draw_t(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.rt(90)
#画T
t.pd()
line(t, l/2)
t.lt(180)
right_angle(t, l/4, l)
#归位
t.pu()
t.rt(90)
line(t, l/4)
t.lt(180)
#U
def draw_u(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.lt(180)
#画U
t.pd()
line(t, l*3/4)
arc(t, l/4, 180)
line(t, l*3/4)
#归位
t.pu()
t.lt(90)
right_angle(t, l/2, l)
t.lt(90)
#V
def draw_v(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.rt(90)
#画V
t.pd()
r_slash(t, 4, l)
l_slash(t, 4, l)
#归位
t.pu()
t.lt(180)
right_angle(t, l/2, l)
t.lt(90)
#W
def draw_w(t, l):
#移动到起点
t.pu()
right_angle(t, l/2, l)
t.lt(180)
#画W
t.pd()
line(t, l)
t.rt(90)
r_slash(t, 2, l/2)
l_slash(t, 2, l/2)
t.rt(90)
line(t, l)
#归位
t.pu()
t.lt(180)
line(t, l)
t.lt(90)
#X
def draw_x(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.rt(90)
#画X
t.pd()
r_slash(t, 2, l)
t.pu()
line(t, -l/2)
t.pd()
l_slash(t, 2, l)
#归位
t.pu()
t.lt(180)
right_angle(t, l/2, l)
t.lt(90)
#Y
def draw_y(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.rt(90)
#画Y
t.pd()
r_slash(t, 1, l/4)
l_slash(t, 1, l/4)
t.pu()
t.lt(180)
right_angle(t, l/4, l/4)
t.pd()
line(t, l/2)
#归位
t.pu()
t.rt(90)
line(t, l/4)
t.lt(180)
#Z
def draw_z(t, l):
#移动到起点
line(t, l/2)
#画Z
t.lt(180)
line(t, l/2)
t.rt(180)
l_slash(t, 2, l)
t.lt(180)
line(t, l/2)
#归位
t.pu()
t.lt(90)
line(t, l)
t.lt(90)
练习 4-5 用函数画阿基米德螺旋
在百度百科阅读关于螺旋线(spiral)的信息,接着编写一段程序来画出阿基米德螺旋(或者其他某种螺旋线)。
![]()
【求解】
Step.1 确认组件
由于《Think Python》到本章为止并没有介绍笛卡尔坐标用法,所以本人不会使用笛卡尔坐标来绘制阿基米德螺旋,本解法基于已经出现过的 polyline 函数实现(绝不超纲)。
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
Step.2 抽象问题
这里提一下 导数 概念:
当函数 y = f ( x ) y=f(x) y=f(x) 的自变量 x x x 在一点 x 0 x_0 x0上产生一个增量 Δ x Δx Δx 时,函数输出值的增量 Δ y Δy Δy 与自变量增量 Δ x Δx Δx 的比值在 Δ x Δx Δx 趋于 0 0 0 时的极限 a a a 如果存在, a a a 即为在 x 0 x_0 x0 处的导数,记作 f ′ ( x 0 ) f'(x_0) f′(x0) 或 d f ( x ) d x ∣ x = x 0 \frac{df(x)}{dx}|_{x=x_0} dxdf(x)∣x=x0。
函数 polyline(t, n, length, angle) 在模拟曲线时,实际上就是画的一小段一小段很短的切线,将精度调整到肉眼看不大出来的时候,画出来就是“曲线”了(实际上,如你所见《Think Python》练习 4-2:用函数画花朵 中的花朵也坑坑洼洼的)。
而我们现在要做的就是:确认一个微小变量(乌龟每次转过的微小角度),根据阿基米德螺旋公式,计算出在这个微小变量下的短小线段的 长度( l l l )。
Step.3 问题求解
已知阿基米德螺公式: r = a + b θ r=a+bθ r=a+bθ
希望乌龟从画布的中间开始画,这样好看点,故去掉起点至画布中心的距离,将阿基米德螺线公式简化为: r = a θ r=aθ r=aθ
![]()
由阿基米德曲线公式 r = a θ r=aθ r=aθ 可知,当角度增加 Δ θ Δθ Δθ,半径从 a θ aθ aθ 变为 a ( θ + Δ θ ) a(θ+Δθ) a(θ+Δθ),即:
r 1 = a θ r_1=aθ r1=aθ
r 2 = a ( θ + Δ θ ) r_2=a(θ+Δθ) r2=a(θ+Δθ)
已知:三角形两边 r 1 r_1 r1、 r 2 r_2 r2 及夹角 Δ θ Δθ Δθ
求:三角形对边 l l l
解:
求高: h = s i n Δ θ ⋅ r ′ = s i n Δ θ ⋅ a ( θ + Δ θ ) h=sinΔθ·r'=sinΔθ·a(θ+Δθ) h=sinΔθ⋅r′=sinΔθ⋅a(θ+Δθ)
求顶点到高的距离与 r 1 r_1 r1 的差: m = c o s Δ θ ⋅ r ′ − r = c o s Δ θ ⋅ a ( θ + Δ θ ) − a θ m =cosΔθ·r'-r=cosΔθ·a(θ+Δθ)-aθ m=cosΔθ⋅r′−r=cosΔθ⋅a(θ+Δθ)−aθ
勾股定理求对边 l l l: l = m 2 + h 2 l=\sqrt{m^2+h^2} l=m2+h2
Step.4 完成代码
"""
《Think Python》练习 4-5:用函数画阿基米德螺旋(蚊香线)
r = aθ
由于用乌龟画,从中间开始旋转比较好看,故没有考虑起点与坐标原点的距离
绘图精度(乌龟每次转过的微小角度):Δθ = π/30 = 6°
绘制的阿基米德螺旋线圈数 (不可能让乌龟无限的画下去):n
theta:阿基米德螺旋角度 θ,从0开始
m:短线条数,根据精度 Δθ 与圈数 n 计算
length:短线长度
angle:短线间的夹角,即精度 Δθ = π/30 = 6°
"""
#引入数学模块、乌龟模块
import math
import turtle
#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01
#阿基米德螺旋
def spiral(t, a, n):
theta = 0
m = int(n * 60)
for i in range(m):
length = math.sqrt( ( math.cos(math.pi/30) * a * ( theta + math.pi/30 ) - a * theta )**2 + ( math.sin(math.pi/30) * a * ( theta + math.pi/30 ) )**2 )
angle = 6
t.fd(length)
t.lt(angle)
theta = theta + math.pi / 30
spiral(bob, 10, 3.25)
turtle.mainloop()
附证明草稿:
![]()
关于《Think Python》课堂笔记&课后作业
报错记录
| 序号 | 报错 | 含义 |
|---|---|---|
| 1 | SyntaxError: Missing parentheses in call to ‘print’. | 语法错误:调用时缺少括号 |
| 2 | SyntaxError: unexpected EOF while parsing | 语法错误:解析时意外终止 |
| 3 | SyntaxError: invalid syntax | 语法错误:无效语法 |
| 4 | SyntaxError: EOL while scanning string literal | 语法错误:扫描字符串时行终止 |
| 5 | NameError: name ‘HolleWorld’ is not defined | 命名错误:命名没有被定义 |
| 6 | SyntaxError: can’t assign to literal | 语法错误:不能赋值给文字 |
更新记录
| 序号 | 更新章节 | 更新时间 |
|---|---|---|
| 1 | 第1章 程序之道(练习 1-1、1-2) | 2019/05/29 |
| 2 | 第2章 变量、表达式和语句(练习 2-1、2-2) | 2019/05/29 |
| 3 | 第3章 函数(练习 3-1、3-2、3-3) | 2019/05/29 |
| 4 | 第4章 案例研究:接口设计(练习 4-1、4-2、4-3) | 2019/05/29 |