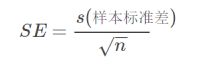统计学和概率论常用的部分基本概念整理
本文梳理了我比较陌生的统计学和概率论的基本概念。目前,只是对基本概念做浅显的理解,通过具体实践练习有了更丰富具体和熟练的认识理解后,随着学习的深入,再深入理解基本概念的深层次含义。某些概念标记为红色文字,即代表一些疑点。
基本概念的框架图:
统计学是在数据分析的基础上,研究测定、收集、整理、归纳和分析反映数据数据,以便给出正确消息的科学。随着大数据时代来临,统计的面貌也逐渐改变,与信息、计算等领域密切结合,是数据科学中的重要主轴之一。
由于它基于观测、重视应用,统计学常被看作是一门独特的数学科学,而不是一个数学分支。很多统计学都不是数学的:如确保所收集来的数据能得出有效的结论;将数据编码、存档以使得信息得以保存,可以在国际上进行比对;汇报结果、总结数据,以便统计员可以明白它们的意思;采取必要措施,保护数据来源对象的隐私。统计学家通过专门的试验设计和调查样本来提升数据质量。统计学自身也为数据的概率模型提供了预测工具。
将数据中的数据模型化,计算它的概率并且做出对于总体的推论被称之为推论统计学。推论是科学进步的重要因素,因为它可能从随机变量中得出数据的结论。推论统计学将命题进行更深入的研究,将结果进行检测。这些都是科学方式的一部分。描述统计学和对新数据的分析更倾向于提供更多的信息,逼近命题所述的真理。
统计学与概率论联系紧密,并常以后者为理论基础。简单地讲,两者不同点在于概率论从总体中推导出样本的概率。统计推论则正好相反——从小的样本中得出大的总体的信息。
描述统计(descriptive statistics),又称叙述统计,是统计学中,来描绘或总结观察量的基本情况的统计总称。其与推论统计相对应。
- 研究者可以透过对数据资料的图像化处理,将资料摘要变为图表,以直观了解整体资料分布的情况。通常会使用的工具是频数分布表与图示法,如多边图、直方图、饼图、散点图等。
- 研究者也可以透过分析数据资料,以了解各变量内的观察值集中与分散的情况。运用的工具有:集中量数,如平均数、中位数、众数、几何平均数、调和平均数。与变异量数,如全距、平均差、标准差、相对差、四分差。
- 在推论统计中,测量样本的集中量数与变异量数都是变量的不偏估计值,但是以平均数、变异数、标准差的有效性最高。
- 数据的次数分配情况,往往会呈现正态分布。为了表示测量数据与正态分布偏离的情况,会使用偏度、峰度这两种统计数据。
- 为了解个别观察值在整体中所占的位置,会需要将观察值转换为相对量数,如百分等级、标准分数、四分位数等。
推断统计学(或称统计推断,英语:statistical inference),指统计学中,研究如何根据样本数据去推断总体数量特征的方法。它是在对样本数据进行描述的基础上,对统计总体的未知数量特征做出以概率形式表述的推断。更概括地说,是在一段有限的时间内,通过对一个随机过程的观察来进行推断。观察者以数据的形态,创建出一个用以解释其随机性和不确定性的数学模型,以之来推论研究中的步骤及总体。
统计检验 A statistical hypothesis, sometimes called confirmatory data analysis, is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables.[1] A statistical hypothesis test is a method of statistical inference. Commonly, two statistical data sets are compared, or a data set obtained by sampling is compared against a synthetic data set from an idealized model. A hypothesis is proposed for the statistical-relationship between the two data-sets, and is compared to an alternative hypothesis, which is an idealized null hypothesis namely which proposes no relationship between these two data-sets. This comparison is deemed statistically significant if the relationship between the data-sets would be an unlikely realization of the null hypothesis according to a threshold probability—the significance level. Hypothesis tests are used when determining what outcomes of a study would lead to a rejection of the null hypothesis for a pre-specified level of significance.
统计检验是一种可基于观察一组随机变量建模过程的可测试的检验,又称验证性数据分析。统计检验是一种统计推断的方法。通常用来检验比较两组抽样数据集,或抽样数据集与建模合成的数据集。统计检验中假设两个数据集之间有统计学关系,和对立的假设——两个数据集之间没有关系的零假设进行比较。如果根据阈值概率(显著性水平),两个数据集之间的关系几乎不可能满足零假设,则假设间的比较被认为是统计学显著的/有统计学意义。统计检验被用于决定一项研究的哪些结局能在预设的显著性水平上拒绝零假设。
——反证法,零假设在极低的概率下才会成立,也就是零假设几乎不会成立,则相反的假设极大概率成立。
零假设(英语:null hypothesis,又译虚无假设、原假设,符号:在推论统计学中,是做统计检验时的一类假设。
零假设的内容一般是希望能证明为错误的假设,与零假设相对的是备择假设(或对立假设),即希望证明是正确的另一种可能。从数学上来看,零假设和备择假设的地位是相等的,但是在统计学的实际运用中,常常需要强调一类假设为应当或期望实现的假设。
如果一个统计检验的结果拒绝零假设(结论不支持零假设),而实际上真实的情况属于零假设,那么称这个检验犯了第一类错误。反之,如果检验结果支持零假设,而实际上真实的情况属于备择假设,那么称这个检验犯了第二类错误。通常的做法是,在保持第一类错误出现的几率在某个特定水平上的时候(即显著性差异值或α值),尽量减少第二类错误出现的概率。
显著性差异(ρ),是统计学上对数据差异性的评价。当数据之间具有了显著性差异,就说明参与比对的数据应该不是来自于同一总体(population),而是来自于具有差异的两个不同总体,换句话说,实验的样本被统计出是有差别的。
通常情况下,实验结果需要证明达到.05水平或.01水平,才可以说数据之间具备了显著性差异,不然就像上述一样做了不精确的推论。在作结论时,应确实描述方向性(例如显著大于或显著小于)。并通常用于假设检验,检验假设和实验结果是否一致。
如果我们是检验某实验(hypothesis test)中测得的数据,那么当数据之间具备显著性差异,实验的零假设就可被推翻,备择假设(alternative hypothesis)则得到支持;反之若数据之间不具备显著性差异,则实验的备择假设可以被推翻,零假设则"不能被推翻"。
测量尺度(scale of measure)或称度量水平(level of measurement)、度量类别,是统计学和定量研究中,对不同种类的数据,依据其尺度水平所划分的类别,这些尺度水平分别为:名目(nominal)、次序(ordinal)、等距(interval)、等比(ratio)。
次序尺度也用来描述一个对象的类别,但与名目尺度不同的是,次序尺度的类别有一定的顺序或大小。次序尺度的变量之间除比较是否相等外,还可以比较大小。但是,加减乘除的运算仍然不能用在次序尺度中。
等距尺度具有次序尺度所有的特性。等距尺度是一组具有连续性、单位又相等的数值,无零点(或零点意义不明确)。如果应用等距尺度来测量变项,乃是依其特征或属性之不同赋予不同的数值。使这些数值不仅显示大小的顺序,而且数值之间具有相等的距离。等距尺度测量值可以相加和相减,其结果仍然有意义。没有绝对零点(0不代表无),正负可同时存在,有顺序,可以比大小,数据的差值有意义,但比例没有意义,可以加减,不能乘除(但可以算平均值)。比如摄氏温度,你可以说20℃比10℃高,且高10℃,但是不能说是两倍,或高一倍。又比如时刻,你可以说两点比一点晚,且晚一小时,但不能说两点是一点的二倍。年份、摄氏温度、华氏温度就是等距尺度。
等比变量具有等距变量的所有特点,同时它也允许乘除运算。大多数物理量,如质量,长度、绝对温度或者能量等等都是等比尺度。等比尺度可以用众数,中位数,算术平均数和几何平均数来描述。
只有等距尺度和等比尺度有计量单位(units of measurement)。
在统计学与概率论中,协方差矩阵(也称离差矩阵、方差-协方差矩阵)是一个矩阵,其 i, j 位置的元素是第 i 个与第 j 个随机变量之间的协方差。这是从标量随机变量到高维度随机向量的自然推广。
在概率论和统计学中,一个离散性随机变量的期望值(或数学期望,亦简称期望,物理学中称为期待值)是试验中每次可能的结果乘以其结果概率的总和。换句话说,期望值像是随机试验在同样的机会下重复多次,所有那些可能状态平均的结果,便基本上等同“期望值”所期望的数。期望值可能与每一个结果都不相等。换句话说,期望值是该变量输出值的加权平均。期望值并不一定包含于其分布值域,也并不一定等于值域平均值。
在数学与统计学中,大数定律又称大数法则、大数律,是描述相当多次数重复实验的结果的定律。根据这个定律知道,样本数量越多,则其算术平均值或样本平均值就有越高的概率接近期望值。
大数定律很重要,因为它“说明”了一些随机事件的均值的长期稳定性。人们发现,在重复试验中,随着试验次数的增加,事件发生的频率趋于一个稳定值;人们同时也发现,在对物理量的测量实践中,测定值的算术平均也具有稳定性。比如,我们向上抛一枚硬币,硬币落下后哪一面朝上是偶然的,但当我们上抛硬币的次数足够多后,达到上万次甚至几十万几百万次以后,我们就会发现,硬币每一面向上的次数约占总次数的二分之一,亦即偶然之中包含着必然。
对任意正数,下式成立:定理表明事件发生的频率依概率收敛于事件的总体概率。定理以严格的数学形式表达了频率的稳定性。就是说当很大时,事件发生的频率于总体概率有较大偏差的可能性很小。
中心极限定理是概率论中的一组定理。中心极限定理说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量之和近似服从正态分布的条件。中心极限定理被认为是(非正式地)概率论中的首席定理。
中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取 n 个抽样,一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。
在实际生活当中,我们不能知道我们想要研究的对象的平均值,标准差之类的统计参数。中心极限定理在理论上保证了我们可以用只抽样一部分的方法,达到推测研究对象统计参数的目的。
在上文的例子中,掷骰子这一行为的理论平均值3.5是我们通过数学定理计算出来的。而我们在实际模拟中,计算出来的样本平均值的平均值(3.48494)确实已经和理论值非常接近了。
大数定理和中心极限定理的关系与区别?
加权平均值即将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数。加权平均值的大小不仅取决于总体中各单位的数值(变量值)的大小,而且取决于各数值出现的次数(频数),由于各数值出现的次数对其在平均数中的影响起着权衡轻重的作用,因此叫做权数。
点估计的含义:是用样本统计量来估计总体参数,因为样本统计量为数轴上某一点值,估计的结果也以一个点的数值表示,所以称为点估计。点估计虽然给出了未知参数的估计值,但是未给出估计值的可靠程度,即估计值偏离未知参数真实值的程度。
接下来看下区间估计:给定置信水平,根据估计值确定真实值可能出现的区间范围,该区间通常以估计值为中心,该区间则为置信区间。
在统计学中,一个概率样本的置信区间(英语:Confidence interval,CI),是对产生这个样本的总体的参数分布(Parametric Distribution)中的某一个未知参数值,以区间形式给出的估计。相对于点估计(Point Estimation)用一个样本统计量来估计参数值,置信区间还蕴含了估计的精确度的信息。在现代机器学习中越来越常用的置信集合(Confidence Set)概念是置信区间在多维分析的推广[1]。
置信区间在频率学派中间使用,其在贝叶斯统计中的对应概念是可信区间(Credible Interval)。两者建立在不同的概念基础上的,贝叶斯统计将分布的位置参数视为随机变量,并对给定观测到的数据之后未知参数的后验分布进行描述,故无论对随机样本还是已观测数据,构造出来的可信区间,其可信水平都是一个合法的概率[2];而置信区间的置信水平,只在考虑随机样本时可以被理解为一个概率。
用中括号[a,b]表示样本估计总体平均值误差范围的区间。a、b的具体数值取决于你对于”该区间包含总体均值”这一结果的可信程度,因此[a,b]被称为置信区间。
一般来说,选定某一个置信区间,我们的目的是为了让”ab之间包含总体平均值”的结果有一特定的概率,这个概率就是所谓的置信水平。例如我们最常用的95%置信水平,就是说做100次抽样,有95次的置信区间包含了总体均值。
标准差是描述一次抽样中的观察值(个体值)之间的变异程度(例如一个人打十次靶子的成绩,这时有一个平均数8,有一个反映他成绩稳定与否的标准差);
标准误差是描述多次抽样的样本均数的抽样误差(例如十次抽样,每次成绩平均数(7,8,6,9,5,6,7,7,8,9)的标准差,也就是抽样分布的标准差);样本的标准误差为:
有95%的样本均值会落在2个(比较精确的值是1.96)标准误差范围内。
在概率论和统计学中,变异系数,又称“离散系数”、“变差系数”(英文:coefficient of variation),是概率分布离散程度的一个归一化量度,其定义为标准差与平均值之比[1]。变异系数(coefficient of variation)只在平均值不为零时有定义,而且一般适用于平均值大于零的情况。变异系数也被称为标准离差率或单位风险。
变异系数只对由等比标量计算出来的数值有意义。举例来说,对于一个气温的分布,使用开尔文或摄氏度来计算的话并不会改变标准差的值,但是温度的平均值会改变,因此使用不同的温标的话得出的变异系数是不同的。也就是说,使用等距变量得到的变异系数是没有意义的。
优点:比起标准差来,变异系数的好处是不需要参照数据的平均值。变异系数是一个无量纲量,因此在比较两组量纲不同或均值不同的数据时,应该用变异系数而不是标准差来作为比较的参考。
缺陷:
- 当平均值接近于0的时候,微小的扰动也会对变异系数产生巨大影响,因此造成精确度不足。
- 变异系数无法发展出类似于均值的置信区间的工具。