LeetCode 55. Jump Game

题目：

给定一个非负整数数组，初始位置是数组的第一个索引。

数组中的每个元素表示该位置的最大跳转长度。

确定是否能够达到最后一个索引。

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

Input: [2,3,1,1,4]         Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.

Input: [3,2,1,0,4]         Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum
             jump length is 0, which makes it impossible to reach the last index.

 

思路：

记录以每个位置结尾，能到达的最远距离，如果在到达数组最后前中断，说明不能到达最后一个索引

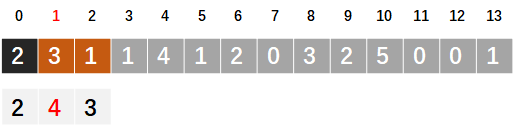
--------   以下图数组为例，从第一个数开始  --------

【0】为2，说明此位置，能到达的最远位置为0+2=2

 

--------  下一步是在0+1~0+2范围内，找该范围中的数，能到达的最远范围  --------

【1】为3，说明此位置，能到达的最远位置为1+3=4；【2】为1，能到达的最远位置为2+1=3；

4＞3，说明，从2位置跳转到【？】再经过一次跳转，可到达的最远距离为4.

 

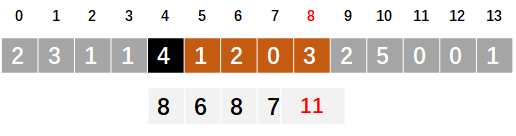
--------  下一步是，从此时的范围的下一个数~此时最远距离4——2+1~4  --------

【3】为1，说明此位置，能到达的最远位置为3+1=4；【4】为4，能到达的最远位置为4+4=8；

8＞4，说明，从2→【3~4】后能到达的最远距离为8

 

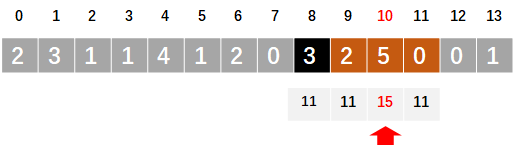
--------  下一步是，从此时的范围的下一个数~此时的最远距离——4+1~8  --------

【5】为1，最远距离5+1=6；【6】为2，最远距离6+2=8；【7】为0，最远距离7+0=0；【8】为3，最远距离8+3=11

11＞8＞7＞6，说明2→【5~8】后，能到达的最远距离为11

 

--------  下一步是，从此时的范围的下一个数~此时的最远距离——8+1~11  --------

【9】为2，最远距离为9+2=11；【10】为5，最远距离为15>13，可到达最后一个索引，返回true

 

【不满足条件的情况】

当在某范围计算时，其范围能到达的最远距离＜=范围index最大值，则表示不能到达最终边界，返回false

 

代码：

class Solution {
    public boolean canJump(int[] nums) {
        if(nums.length==0) {
            return false;
        }
        
        if(nums[0]>=nums.length-1) {
            return true;
        }
    	
        int[] path = new int[nums.length];
        path[0] = nums[0];
        
        int start = 0;
        int end = path[start];
        int farthest = start;
        
        // 依次对每个范围进行查找
        while(farthest!=-1 && path[farthest] < nums.length-1) {
            end = path[farthest];
            farthest = farthestJump(nums, path, start,end);
            start =  end;
        }
        
        if(farthest==-1) {
            return false;
        }else {
            return true;
        }
    }
    
    
    public int farthestJump(int[] nums,int[] path,int start,int end) {
        int maxIndex = start;
        int init = start;
        
        // 更新当前范围内 每个位置能到达的最远距离，并用maxIndex记录
        while(start<=end) {
            path[start] = start + nums[start];
            if(path[start]>path[maxIndex]) {
                maxIndex = start;
            }
            start++;
        }
    	
        // 如果最远距离不超过当前范围，则返回-1
        // 否则返回下一个范围的边界index
        if(maxIndex!=init) {
            return maxIndex;
        }else {
            return -1;
        }
    }
}