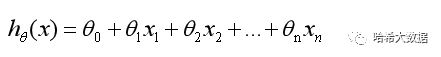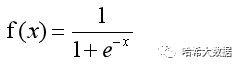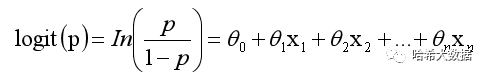欢迎大家关注公众号【哈希大数据】
1、二元分类问题概述
机器学习可以实现的两大核心点是分类预测和回归预测。在之前的分享中我们介绍了连续数据的线性回归预测问题。但是在实际生活中,我们所面对的许多问题往往是非连续的分类问题,比如医生根据一些指标判断病人是否可以康复、企业根据用户行为分析用户是否会流失、警察根据嫌疑人的特征来判定其是否为罪犯等。这些只有“是、否”两种结果的问题均属于两元分类问题。
在机器学习中,存在许多预测分类的算法,包括逻辑回归、决策树、支持向量机、随机森林、神经网络、朴素贝叶斯分类等等。其中逻辑回归是基于线性回归发展而来的,因其预测较为准确、易于理解而广泛应用于实际场景中,比如在银行的相关业务中,有80%是通过逻辑回归进行预测的,因此本节我们将从理论到具体实现,来详细讲解逻辑回归的相关内容。而具体案例应用将稍后分享。
2、逻辑回归介绍
我们已知常规的线性回归问题是寻找多个特征x和目标变量之间的线性关系,具体计算模型为:
在这种情况下,所得到的目标变量是连续的一些值。在实际问题中,虽然我们拥有同样多的特征属性值x,但是其目标却只有(是、否)两种情况。显然上述的线性问题无法与目标拟合,因此我们希望,可以做个同等变换将使这些连续的值,与分类结果相关联。这种关联方式可以通过Sigmoid函数来实现:
即当x为0.5时其值为0,大于0.5时其值将不断增大到无限接近于1,反之将接近0。下图表示x在不同范围时的函数值。
因此我们在原本的线性回归模型中套用Sigmoid函数就可以构建出逻辑回归的具体模型P:这样便可以表示预测结果为其中一种情况的可能性为p。
该逻辑回归模型等价与logit(p),这样便可以实现将连续的值映射为表示分类的概率问题。
构建完模型后,在进行机器学习预测时,我们也需要设计模型参数的计算方式,通过定义损失函数来确定参数值进而实现准确的预测。具体损失函数的构建以及参数值的优化(可使用梯度下降、牛顿法、拟牛顿法、梯度上升)等的具体实现,涉及到大量的数学计算这里将不再进行详细推导,如果感兴趣的小伙伴欢迎留言讨论。下面我们将具体通过python来一步步完成逻辑回归预测。
2、python从零实现逻辑回归
python的Scikit-learn库中已有完整的逻辑回归算法,类似于之前讲解的线性回归模型,可以直接导入后直接使用。具体导入方式如下。
from sklearn.linear_modle import LogisticRegression
但是为了更好的理解逻辑回归的实现思路,本次我们将从零实现该算法。
首先生成Logistic的一个类方法,第一步是实现特征变量x和分类变量y的初始化。
class logistic():
def __init__(self, x, y):
if type(x) == type(y) == list:
self.x = np.array(x)
self.y = np.array(y)
elif type(x) == type(y) == np.ndarray:
self.x = x
self.y = y
else: raise False
第二步:定义sigmoid函数,完成调用可返回计算后的结果值。
def sigmoid(num):
if type(num) == int or type(num) == float:
return 1.0 / (1 + exp(-1 * num))
else: raise False
第三步:进行数据的训练。其中alpha为学习率,errors为迭代阈值(只有计算误差小于该值才会停止训练),punish为惩罚系数默认为0.0001,times表示最大迭代次数。
def train_data(self, alpha, errors, punish=0.0001):
self.punish = punish
dimension = self.x.shape[1]
self.theta = np.random.random(dimension)
compute_error = 100000000
times = 0
while compute_error > errors:
res = np.dot(self.x, self.theta)
delta = self.sigmoid(res) - self.y
self.theta = self.theta - alpha * np.dot(self.x.T, delta) - punish * self.theta # 带惩罚的梯度下降方法
compute_error = np.sum(delta)
times += 1
第四步:对新的数据进行结果预测,返回0或者1的预测结果(将实际问题数据化处理)
def predict(self, x):
x = np.array(x)
if self.sigmoid(np.dot(x, self.theta)) > 0.5:
return 1 else: return 0
至此逻辑回归的预测算法已经实现,为了检验我们实现的该算法的准确性,我们将通过随机生成一些分类变量来进行测试。
首先生成200条2分类数据:
x, y = make_blobs(n_samples=200, centers=2, n_features=2, random_state=0, center_box=(10, 20))
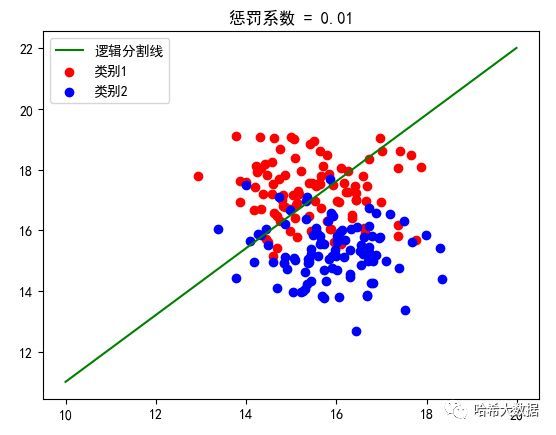
然后调用我们完成的逻辑回归算法:(分别指定惩罚系数为0.1和0.01)
result = logistic(x, y)
result.train_data(alpha=0.00001, errors=0.005, punish=0.01)
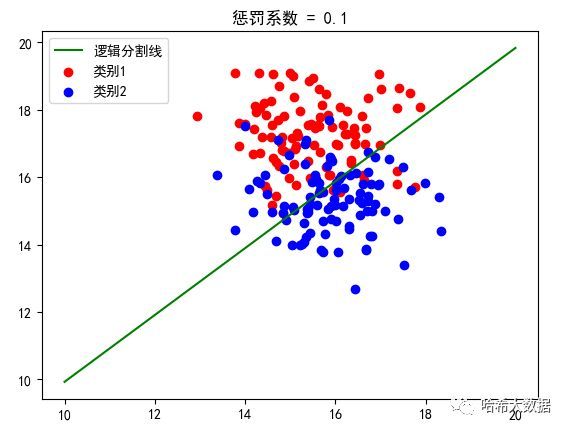
分类预测效果展示:
我们明显可以看出不同惩罚参数的逻辑分割线是不同的,因此这也充分表明需要根据数据的实际特征来设定惩罚的系数,进而是预测结果可以更加准确。