【Python机器学习预测分析算法实战七】集成算法
集成算法(Emseble Learning)是构建多个学习器,然后通过一定策略结合把它们来完成学习任务的,常常可以获得比单一学习显著优越的学习器。
集成方法是由两层算法组成的层次架构。底层算法叫做基学习器。基学习器是单个机器学习算法,这些算法在后续会被集成到一个集成方法中。决策树是最常用的基学习器之一。目前广泛使用的上层算法主要有:投票(bagging)、提升(boosting)、随机森林(random forests)。
基分类器——二元决策树
决策树呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。学习时,利用训练数据,根据损失函数最小化的原则建立决策树模型;预测时,对新的数据,利用决策模型进行分类。
决策树的几个重要概念定义:
(1)根结点(Root Node):它表示整个样本集合,并且该节点可以进一步划分成两个或多个子集。
(2)拆分(Splitting):表示将一个结点拆分成多个子集的过程。
(3)决策结点(Decision Node):当一个子结点进一步被拆分成多个子节点时,这个子节点就叫做决策结点。
(4)叶子结点(Leaf/Terminal Node):无法再拆分的结点被称为叶子结点。
(5)剪枝(Pruning):移除决策树中子结点的过程就叫做剪枝,跟拆分过程相反。
(6)分支/子树(Branch/Sub-Tree):一棵决策树的一部分就叫做分支或子树。
(7)父结点和子结点(Paren and Child Node):一个结点被拆分成多个子节点,这个结点就叫做父节点;其拆分后的子结点也叫做子结点。
决策树的构造过程一般分为3个部分,分别是特征选择、决策树生产和决策树裁剪。
(1)特征选择:
特征选择表示从众多的特征中选择一个特征作为当前节点分裂的标准,如何选择特征有不同的量化评估方法,从而衍生出不同的决策树,如ID3(通过信息增益选择特征)、C4.5(通过信息增益比选择特征)、CART(通过Gini指数选择特征)等。
目的(准则):使用某特征对数据集划分之后,各数据子集的纯度要比划分钱的数据集D的纯度高(也就是不确定性要比划分前数据集D的不确定性低)
(2)决策树的生成
根据选择的特征评估标准,从上至下递归地生成子节点,直到数据集不可分则停止决策树停止生长。这个过程实际上就是使用满足划分准则的特征不断的将数据集划分成纯度更高,不确定行更小的子集的过程。对于当前数据集的每一次划分,都希望根据某个特征划分之后的各个子集的纯度更高,不确定性更小。
(3)决策树的裁剪
决策树容易过拟合,一般需要剪枝来缩小树结构规模、缓解过拟合。
决策树算法有很多变种,包括ID3、C4.5、CART等,但其基础都是类似的。属性选择方法总是选择最好的属性最为分裂属性,即让每个分支的记录的类别尽可能纯。它将所有属性列表的属性进行按某个标准排序,从而选出最好的属性。属性选择方法很多,三个常用的方法:信息增益(Information gain)、增益比率(gain ratio)、基尼指数(Gini index)。这里不对决策树算法做更详细的解释。
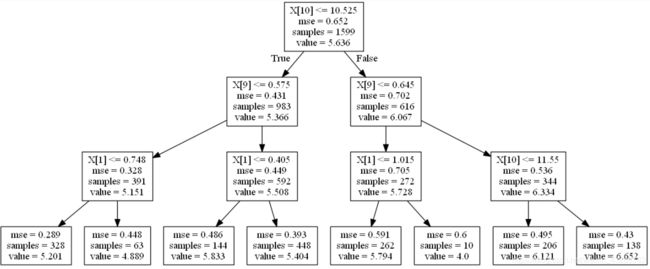
下面例子是决策树的一个例子;
import urllib.request, urllib.error, urllib.parse
import numpy
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
from sklearn.externals.six import StringIO
from math import sqrt
import matplotlib.pyplot as plot
#读取数据
target_url = "http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv"
data = urllib.request.urlopen(target_url)
xList = []
labels = []
names = []
firstLine = True
for line in data:
if firstLine:
names = line.decode().strip().split(";")
firstLine = False
else:
#冒号分割
row = line.decode().strip().split(";")
#分割标签
labels.append(float(row[-1]))
#移除标签
row.pop()
#转为浮点型
floatRow = [float(num) for num in row]
xList.append(floatRow)
nrows = len(xList)
ncols = len(xList[0])
wineTree = DecisionTreeRegressor(max_depth=3)
wineTree.fit(xList, labels)
with open("wineTree.dot", 'w') as f:
f = tree.export_graphviz(wineTree, out_file=f)
#Note: The code above exports the trained tree info to a Graphviz "dot" file.
#打开命令提示符,输入决策树图片存放路径,然后键入下面代码打印图片
#dot -Tpng wineTree.dot -o wineTree.png
集成算法之bagging
Bagging中文叫做自举集成(booststrap aggregation),booststrap是一种取样方法,通常用来从一个中等规模数据集中产生取样统计。一个booststrap取样是从数据集中有放回式的随机选取元素(也就是说,booststrap可能会重复取出原始数据中的同一行数据)。Bagging算法从训练数据中获得一系列的booststrap样本,然后针对每一个booststrap样本训练一个基学习器。对于回归问题,结果是机器学习的均值;对于分类问题,结果是从不同类别所占百分比引申出来的各种类别的概率或者均值。
Bagging集成算法的子问题是从原始训练数据中采取booststrap方法取样产生的。Bagging方法可以减少单个二元决策树的方差。为了保证效果,Bagging方法采用的决策树需要具有足够的深度。
import urllib.request, urllib.error, urllib.parse
import numpy
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
import random
from math import sqrt
import matplotlib.pyplot as plot
#read data into iterable
target_url = "http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv"
data = urllib.request.urlopen(target_url)
xList = []
labels = []
names = []
firstLine = True
for line in data:
if firstLine:
names = line.decode().strip().split(";")
firstLine = False
else:
#split on semi-colon
row = line.decode().strip().split(";")
#put labels in separate array
labels.append(float(row[-1]))
#remove label from row
row.pop()
#convert row to floats
floatRow = [float(num) for num in row]
xList.append(floatRow)
nrows = len(xList)
ncols = len(xList[0])
#take fixed test set 30% of sample
random.seed(1)
nSample = int(nrows * 0.30)
idxTest = random.sample(range(nrows), nSample)
idxTest.sort()
idxTrain = [idx for idx in range(nrows) if not(idx in idxTest)]
#Define test and training attribute and label sets
xTrain = [xList[r] for r in idxTrain]
xTest = [xList[r] for r in idxTest]
yTrain = [labels[r] for r in idxTrain]
yTest = [labels[r] for r in idxTest]
#train a series of models on random subsets of the training data
#collect the models in a list and check error of composite as list grows
#maximum number of models to generate
numTreesMax = 30
#tree depth - typically at the high end
treeDepth = 1
#initialize a list to hold models
modelList = []
predList = []
#number of samples to draw for stochastic bagging
nBagSamples = int(len(xTrain) * 0.5)
for iTrees in range(numTreesMax):
idxBag = []
for i in range(nBagSamples):
idxBag.append(random.choice(range(len(xTrain))))
xTrainBag = [xTrain[i] for i in idxBag]
yTrainBag = [yTrain[i] for i in idxBag]
modelList.append(DecisionTreeRegressor(max_depth=treeDepth))
modelList[-1].fit(xTrainBag, yTrainBag)
#make prediction with latest model and add to list of predictions
latestPrediction = modelList[-1].predict(xTest)
predList.append(list(latestPrediction))
#build cumulative prediction from first "n" models
mse = []
allPredictions = []
for iModels in range(len(modelList)):
#average first "iModels" of the predictions
prediction = []
for iPred in range(len(xTest)):
prediction.append(sum([predList[i][iPred] for i in range(iModels + 1)])/(iModels + 1))
allPredictions.append(prediction)
errors = [(yTest[i] - prediction[i]) for i in range(len(yTest))]
mse.append(sum([e * e for e in errors]) / len(yTest))
nModels = [i + 1 for i in range(len(modelList))]
plot.plot(nModels,mse)
plot.axis('tight')
plot.xlabel('Number of Tree Models in Ensemble')
plot.ylabel('Mean Squared Error')
plot.ylim((0.0, max(mse)))
plot.show()
print('Minimum MSE')
print(min(mse))
#with treeDepth = 1
#Minimum MSE
#0.516236026081
#with treeDepth = 5
#Minimum MSE
#0.39815421341
#with treeDepth = 12 & numTreesMax = 100
#Minimum MSE
#0.350749027669
集成算法之梯度提升法(Gradient boosting)
梯度提升法是基于决策树的集成方法,在不同标签上训练决策树,然后将其组合起来。对于回归问题,目标是最小化均方误差,每个后续的决策树是在前面的决策树遗留的错误上进行训练。
Bagging和梯度提升法在工作原理上的根本差异在于梯度提升法持续监测自己的累计误差,然后使用残差进行训练。这种根本差异也解释了为什么当问题属性之间存在强的相互依赖、相互作用时,梯度提升法只需要调整决策树的深度。
import urllib.request, urllib.error, urllib.parse
import numpy
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
import random
from math import sqrt
import matplotlib.pyplot as plot
#read data into iterable
target_url = "http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv"
data = urllib.request.urlopen(target_url)
xList = []
labels = []
names = []
firstLine = True
for line in data:
if firstLine:
names = line.decode().strip().split(";")
firstLine = False
else:
#split on semi-colon
row = line.decode().strip().split(";")
#put labels in separate array
labels.append(float(row[-1]))
#remove label from row
row.pop()
#convert row to floats
floatRow = [float(num) for num in row]
xList.append(floatRow)
nrows = len(xList)
ncols = len(xList[0])
#take fixed test set 30% of sample
nSample = int(nrows * 0.30)
idxTest = random.sample(range(nrows), nSample)
idxTest.sort()
idxTrain = [idx for idx in range(nrows) if not(idx in idxTest)]
#Define test and training attribute and label sets
xTrain = [xList[r] for r in idxTrain]
xTest = [xList[r] for r in idxTest]
yTrain = [labels[r] for r in idxTrain]
yTest = [labels[r] for r in idxTest]
#train a series of models on random subsets of the training data
#collect the models in a list and check error of composite as list grows
#maximum number of models to generate
numTreesMax = 30
#tree depth - typically at the high end
treeDepth = 5
#initialize a list to hold models
modelList = []
predList = []
eps = 0.1
#initialize residuals to be the labels y
residuals = list(yTrain)
for iTrees in range(numTreesMax):
modelList.append(DecisionTreeRegressor(max_depth=treeDepth))
modelList[-1].fit(xTrain, residuals)
#make prediction with latest model and add to list of predictions
latestInSamplePrediction = modelList[-1].predict(xTrain)
#use new predictions to update residuals
residuals = [residuals[i] - eps * latestInSamplePrediction[i] for i in range(len(residuals))]
latestOutSamplePrediction = modelList[-1].predict(xTest)
predList.append(list(latestOutSamplePrediction))
#build cumulative prediction from first "n" models
mse = []
allPredictions = []
for iModels in range(len(modelList)):
#add the first "iModels" of the predictions and multiply by eps
prediction = []
for iPred in range(len(xTest)):
prediction.append(sum([predList[i][iPred] for i in range(iModels + 1)]) * eps)
allPredictions.append(prediction)
errors = [(yTest[i] - prediction[i]) for i in range(len(yTest))]
mse.append(sum([e * e for e in errors]) / len(yTest))
nModels = [i + 1 for i in range(len(modelList))]
plot.plot(nModels,mse)
plot.axis('tight')
plot.xlabel('Number of Trees in Ensemble')
plot.ylabel('Mean Squared Error')
plot.ylim((0.0, max(mse)))
plot.show()
print('Minimum MSE')
print(min(mse))
#printed output
#Minimum MSE
#0.405031864814
集成算法之随机森林
随机森林在数据集的子集上训练处一系列的模型。这些子集是从全训练数据集中随机抽取的。一种抽取方式是对数据进行随机放回取样,与Bagging相同,另一种方法是每个决策树的训练数据集只是所有属性随机抽取的一个子集,而不是全部属性。
随机森林是Bagging和boosting两种方法的结合,包括了Bagging方法和属性随机选择方法。属性随机选择实际上是对二元决策树及学习器的修正。这些差异看起来不是本质上的,但是这些给予了随机森林与Bagging和梯度提升算法不同的性能特征。有研究显示,随机森林更适合用于广泛稀疏的属性空间,如文本挖掘问题。与梯度提升算法相比,随机森林更易于并行化,因为每个基学习器都可以单独训练。而梯度提升算法不行,因为每个基学习器都依赖于前一个基学习器的结果。
import urllib.request, urllib.error, urllib.parse
import numpy
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
import random
from math import sqrt
import matplotlib.pyplot as plot
#read data into iterable
target_url = "http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv"
data = urllib.request.urlopen(target_url)
xList = []
labels = []
names = []
firstLine = True
for line in data:
if firstLine:
names = line.decode().strip().split(";")
firstLine = False
else:
#split on semi-colon
row = line.decode().strip().split(";")
#put labels in separate array
labels.append(float(row[-1]))
#remove label from row
row.pop()
#convert row to floats
floatRow = [float(num) for num in row]
xList.append(floatRow)
nrows = len(xList)
ncols = len(xList[0])
#take fixed test set 30% of sample
random.seed(1) #set seed so results are the same each run
nSample = int(nrows * 0.30)
idxTest = random.sample(range(nrows), nSample)
idxTest.sort()
idxTrain = [idx for idx in range(nrows) if not(idx in idxTest)]
#Define test and training attribute and label sets
xTrain = [xList[r] for r in idxTrain]
xTest = [xList[r] for r in idxTest]
yTrain = [labels[r] for r in idxTrain]
yTest = [labels[r] for r in idxTest]
#train a series of models on random subsets of the training data
#collect the models in a list and check error of composite as list grows
#maximum number of models to generate
numTreesMax = 30
#tree depth - typically at the high end
treeDepth = 12
#pick how many attributes will be used in each model.
# authors recommend 1/3 for regression problem
nAttr = 4
#initialize a list to hold models
modelList = []
indexList = []
predList = []
nTrainRows = len(yTrain)
for iTrees in range(numTreesMax):
modelList.append(DecisionTreeRegressor(max_depth=treeDepth))
#take random sample of attributes
idxAttr = random.sample(range(ncols), nAttr)
idxAttr.sort()
indexList.append(idxAttr)
#take a random sample of training rows
idxRows = []
for i in range(int(0.5 * nTrainRows)):
idxRows.append(random.choice(range(len(xTrain))))
idxRows.sort()
#build training set
xRfTrain = []
yRfTrain = []
for i in range(len(idxRows)):
temp = [xTrain[idxRows[i]][j] for j in idxAttr]
xRfTrain.append(temp)
yRfTrain.append(yTrain[idxRows[i]])
modelList[-1].fit(xRfTrain, yRfTrain)
#restrict xTest to attributes selected for training
xRfTest = []
for xx in xTest:
temp = [xx[i] for i in idxAttr]
xRfTest.append(temp)
latestOutSamplePrediction = modelList[-1].predict(xRfTest)
predList.append(list(latestOutSamplePrediction))
#build cumulative prediction from first "n" models
mse = []
allPredictions = []
for iModels in range(len(modelList)):
#add the first "iModels" of the predictions and multiply by eps
prediction = []
for iPred in range(len(xTest)):
prediction.append(sum([predList[i][iPred] for i in range(iModels + 1)]) / (iModels + 1))
allPredictions.append(prediction)
errors = [(yTest[i] - prediction[i]) for i in range(len(yTest))]
mse.append(sum([e * e for e in errors]) / len(yTest))
nModels = [i + 1 for i in range(len(modelList))]
plot.plot(nModels,mse)
plot.axis('tight')
plot.xlabel('Number of Trees in Ensemble')
plot.ylabel('Mean Squared Error')
plot.ylim((0.0, max(mse)))
plot.show()
print('Minimum MSE')
print(min(mse))
#printed output
#Depth 1
#Minimum MSE
#0.52666715461
#Depth 5
#Minimum MSE
#0.426116327584
#Depth 12
#Minimum MSE
#0.38508387863
All things are difficult before they are easy.