LeetCode最长上升子序列（Java）

来源：LeetCode–300
难度：中等
解题方法：Java

题目要求：给定一个无序的整数数组，找到其中最长上升子序列的长度。

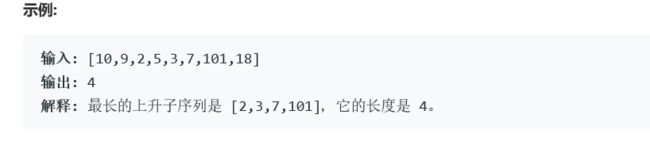
说明:

• 可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
• 你算法的时间复杂度应该为 O(n2) 。

进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?

思路分析

• 我们可以定义一个变量temp，用来存储到目前为止的最长上升子序列的长度。
• 这里的最长上升子序列不一定是连续的，因此无法单独的采用一个数来进行存储。我们可以采用一个和原数组长度相同的数组dp[]，数组中的元素是原数组元素对应的最长子序列的长度。
• 采用动态规划的思路，第i个元素的最长上升子串与它前面每一个比它小的元素的最长上升子串有关。第i个元素的最长子序列=第j个元素的最长子序列+1（其中j
• 寻找一个中间变量，将dp[]中的最大值存储下来，就是我们要找的最长上升子串的长度。

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = 0;
        int[] dp= new int[nums.length];
        Arrays.fill(dp,1);
        //新建一个数组，里面存的是该点的最长上升子序列的个数
        for(int i=0;i<nums.length;i++){
            for(int j=0;j<i;j++){
                if(nums[j]<nums[i]){
                    dp[i] =Math.max(dp[j]+1,dp[i]) ; 
                    //更新最长上升子序列，储存可能的上升子序列中的最大值  
                }
            }
            len = Math.max(dp[i],len);
            //len用来储存所有元素中最大子序列的长度
        }
        return len;
    }
}

进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?

思路：上面解法的时间复杂度是n^2，为了降低时间复杂度，我们可以维护一个严格递增的子序列。在不改变子序列长度的条件下，将子序列中的数换成尽可能小的数，因为这个子序列中的数越小，它越容易被延长。

【例】一个数组为[1,3,7,2,4,5]
它为[1]时，它的最长子序列为[1]
它为[1,3]时，它的最长子序列为[1,3]
它为[1,3,7]时，它的最长子序列为[1,3,7]
它为[1,3,7,2]时，它的最长子序列为[1,2,7]，因为[1,2]比[1,3]更容易增长，所以如果子序列数组中有比新增元素(n)大的数(m)，我们要将m替换成n。这里替换的是大于n且与m差值最小的数，这样子序列增长的可能性会更大。
它为[1,3,7,2,4]时，它的最长子序列为[1,2,4]
他为[1,3,7,2,4,5]时，它的最长子序列为[1,2,4,5],如果我们之前不更新最长子序列，这里就无法把5加进去

class Solution {
    public int lengthOfLIS(int[] nums) {
          int len = 0;
        int[] dp= new int[nums.length];
        for (int num : nums) {
            int i = Arrays.binarySearch(dp, 0, len, num);
            //二分法，如果没有该元素，返回的是-（插入点）-1
            if (i<0) {
                i= -(i+1);
                //i为插入点的位置
            }
            dp[i] = num;
            //将num插入
            if (i==len) {
                len++;
                //如果num插在最后面，则长度+1
            }
        }
        return len;
    }
}