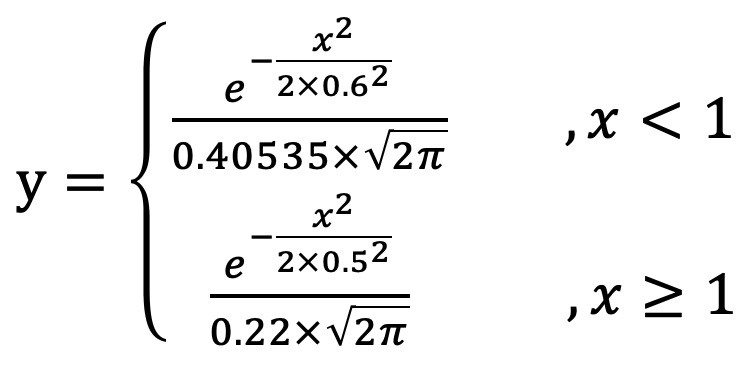抽空整理了一些工作中做策略时常用到的函数类型,并画出了各种函数的分布图,在设计策略时可根据某个数据项的期望影响值来匹配相应的函数即可。
一、对数函数
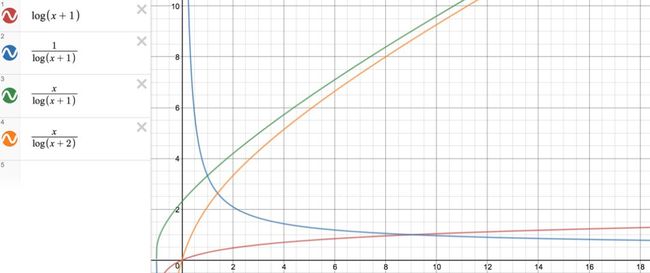
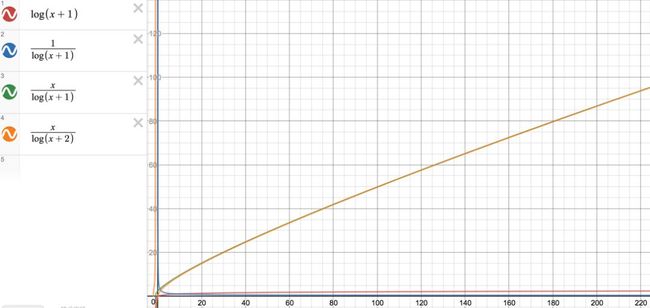
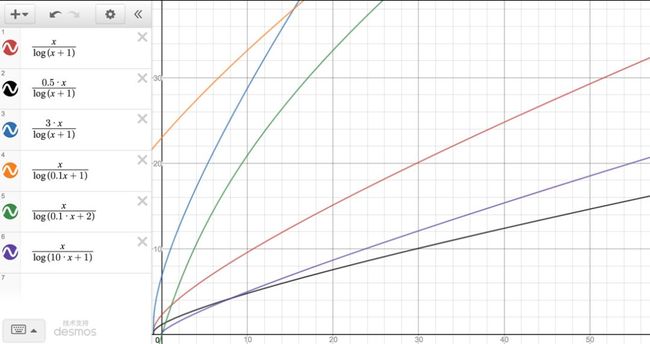
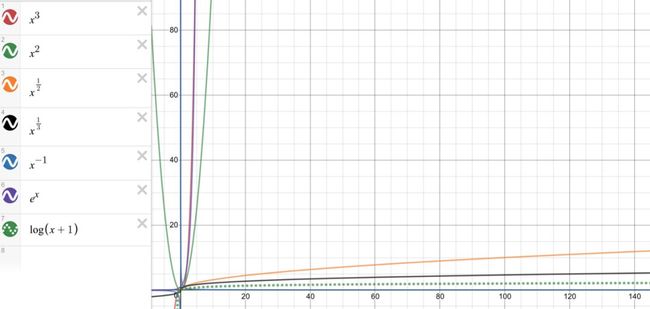
常见的几种对数函数曲线如下:
由上面两图可以看出这几个函数的一些特点:
1、当x=0时,y=log(x+1)和y=x/log(x+2)都为0,y=x/log(x+1)的值为ln(10);
2、随着x的增加,y=x/log(x+1)和y=x/log(x+2)的变化趋势一致,且曲线看上去几乎为一条;
3、y=log(x+1)的曲线始终贴着x轴在延伸。当x较小时,y=log(x+1)的变化较大;当x不断增大时,函数曲线变化得越来越慢。
对数函数在工作中的常见应用:
1、比如我们希望视频的播放量达到某个阈值后,它后续是否还有增加,以及增加幅度的大小我们不再关心;但在未达到该阈值前,视频的每一次播放都会对召回或排序环节有明显的影响。这样的场景需求可以考虑对数函数来处理(如log(x+1))。
2、比如在播放量增长的前期能明确反应出用户对该视频的有兴趣,即使数量小,也希望将该兴趣放大;但随着时间的推移,播放量会不断增加,而我们并不想播放量大的视频一直霸占着头版,其他视频没有机会展露头角。这类场景下也可以用对数函数来处理(如1/(1+log(x)))。
在具体应用中也可基于业务场景对函数的参数进行适当调整,下面可以详细看下各类函数在不同参数下的变化。
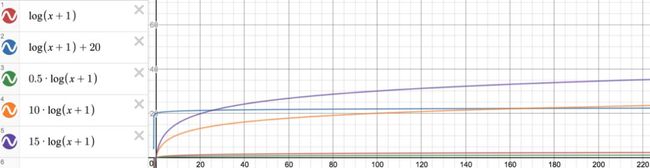
1)y=A*log(x+1)+C
如Fig3所示:
1、当x较小时,A可用来调节函数的凸度,A越大函数的曲线越凸;
2、当x较大时(即函数趋于稳定时),A越大,离x轴越远;
3、C可用来上下平移。
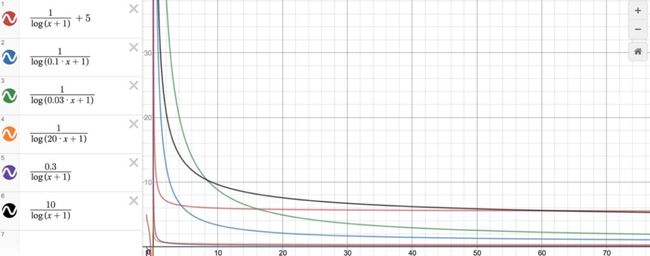
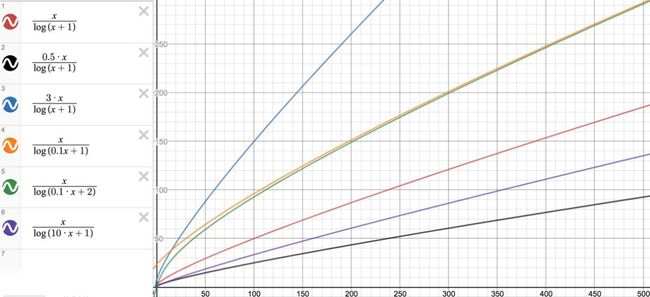
2)y=A/log(Bx+1)+C
如Fig4所示:
1、A可用来调节曲线与x轴的距离,A越大曲线离x轴越远,但与y轴的距离变化不大;
2、B可用来调节函数凹点离原点的距离,B越小,曲线离原点越远,凹度越小,且离x和y轴的距离几乎相同;B越大,曲线离原点越近,凹度越大,但曲线靠近y轴的速度要大于靠近x轴的速度;
3、C可用来上下平移。
3)y= A*x/log(Bx+1)+C
如Fig5、Fig6所示:
1、A可用来调节曲线与x轴的距离,A越大,曲线离x轴越远;x=0处;
2、B可用来调节x=0时,y值离原点的距离;B越大,x=0时的y值越大(也可以用A来调节,但A增大的同时,曲线远离x轴的增速远大于离原点的增速);
3、曲线x/log(x+1)不过原点,曲线x/log(x+2)会过原点
4、C可用来上下平移。
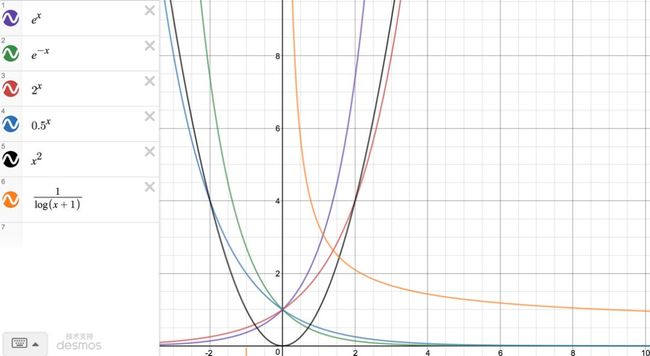
二、指数函数
指数函数在策略中用的不多,但基于指数函数的变形函数却很好用,例如sigmoid函数:1/(1+e^(-x)),其在机器学习及神经网络中就有广泛的使用。
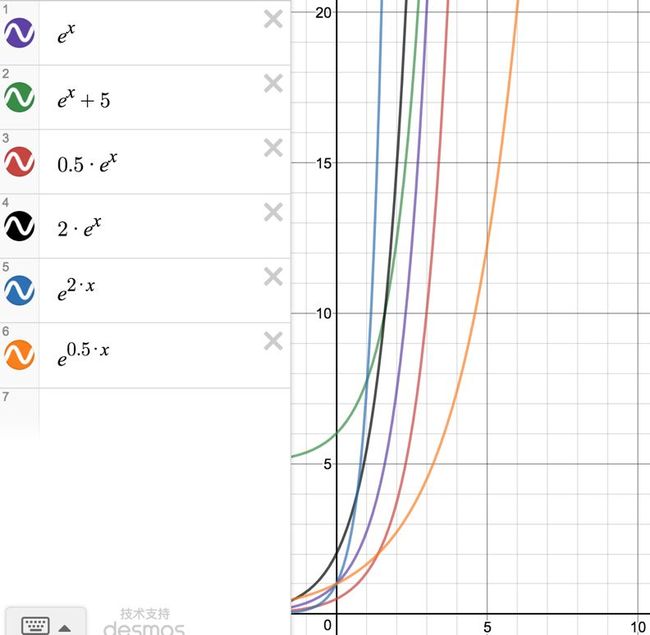
下图是不同参数的指数函数曲线的变化趋势。
从Fig7.可以看出:
1、A可以用来调整与y轴的交点的大小,同时保持曲线调整前后的相对位置不变;
2、B可用来调节曲线与y轴的距离,B越大,曲线离y轴越近。
3、C可用来上下平移。
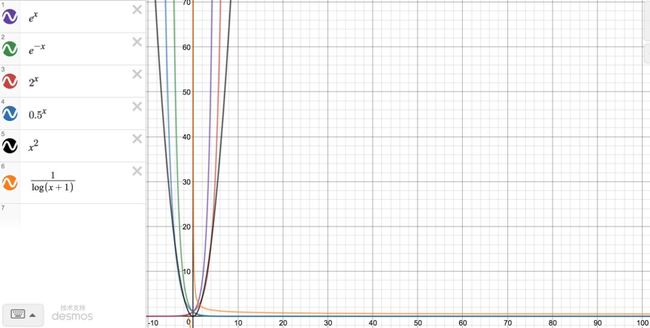
三、幂函数
在策略中比较常见的是开根号和开平方的形式,这类函数经常被用在需打压或增强某个指标影响面的策略中。
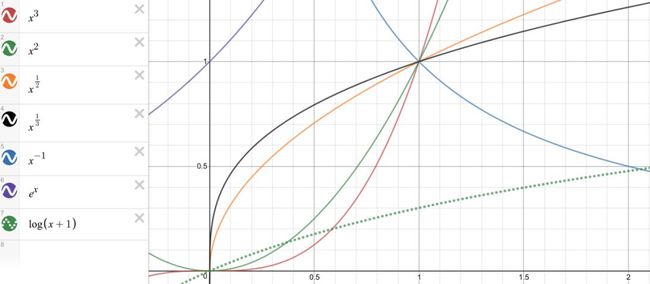
下图分别显示了各类幂函数的曲线变化,及相互关系。
从图Fig8、Fig9中可以看出其变化趋势:
1、当幂小于1时,幂的值越小,曲线离x轴越近;当幂大于1时,幂的值越大,曲线离y轴越近;
2、当变量在[0,1]范围且变量间的差很小时,指数函数是用来做区分度较好的选择。当变量聚集在[0,0.5],可选择幂小于1的数;当变量聚集在[0.5,1],可选择幂大于1的数。
ps:图Fig9中也加入了指数函数,可以看出e^x和x^3大概在[1.86,6.41]和[4.5,93.4]相交,即x在[1.86,4.5]时,x^3的值大于e^x。
幂函数的常见应用:
1、从Fig8可以想到,若某个指标x在[0,1]范围内,可以通过控制幂的大小,扩大/缩小该指标的区分度。如各视频在某项的打分上太相似,无法区分孰优孰劣,可以对该指标归一化在[0,1],并根据预期的区分效果取幂的值。
2、从Fig9可以看出,幂函数还可以用在抑制某类数值过度增大的场景,并将其限制在较小的范围内,缓慢增加。
将三类函数的曲线画在一起后,它们的相对关系如下图:
从Fig10.和Fig11.可以看出:
1、y=x²,y=x^3,y=x^(1/3)和y=x^(1/2)的自变量在正数区间内, e^x、2^x和x^2的变化趋势相近,e^(-x)、x^(1/2)和1/log(x+1)的变化趋势相近。
2、2^x和x^2在[2,4]和[4,16]相交,即x在[2,4]时,x^2的值大于2^x。
四、其他函数
除了以上常见的基础函数外,还有些其他的函数也会在策略中时常用到,如取值范围在[-1,1]的双曲正切函数tanh(x)和阶跃函数sgn(x),取值范围在[0,1]的sigmoid函数等有界函数。
此外,在工作中遇到的问题并不是都能用以上这些基础函数解决,实际问题的解决难度也会随业务的复杂度而增加,这就需要将这些基础函数综合运用,来达到我们期望的目标。
比如我们在给用户推荐视频,或推荐某个作者发布的视频时,希望最新发布的好视频能优先展现给用户,这需要在考虑用户反馈的基础上加入时间衰减的因子。这样优化后,即使某个视频的用户反馈好,CTR很高,若不是新视频,排序也会相应靠后,把前面的位置留给最新发布且当前效果好的视频。
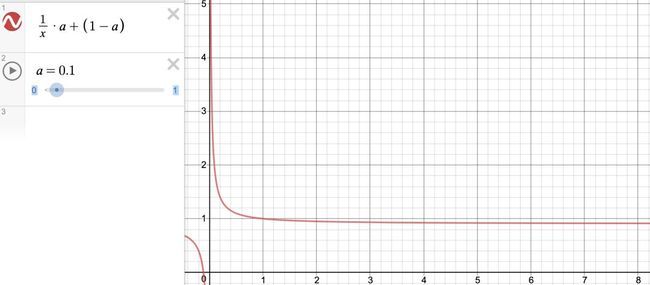
时间衰减的方法有很多,比较著名的是牛顿冷却公式(想了解的可看这篇:https://www.zybuluo.com/evilking/note/1029052)。当然我们也可以通过以上基础函数结合具体需求组合出我们想要的公式,如下面两个公式:
1、以幂函数为基础
从上图可以看出,当时间差在1天内,呈指数级衰减;时间差大于1天后,衰减变缓慢(在a=0.1的条件下,几乎没有差别)。这在实时性要求较高的场景下非常好用,有新视频产生时,会很快被推荐出来。
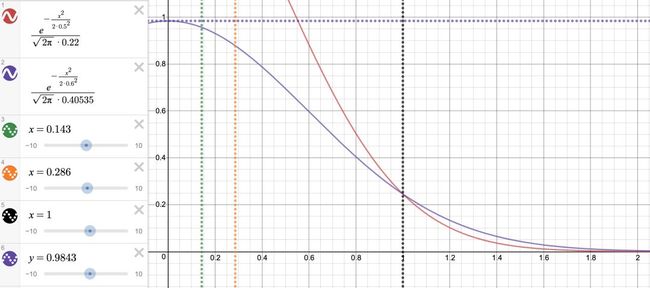
2、以指数函数和幂函数为基础
其中,绿虚线是24h,橘虚线是48h,黑虚线是7天。
从图中可以看出,24h内的衰减很慢,几分钟和几小时差别不大,24h到48h内,衰减幅度开始增加,超过7天的衰减是呈指数级的变化趋势。这可以鼓励作者每周至少发布一条内容,且需要持续更新才会有稳定的流量。平台会优先把流量给新发布的视频,而超过7天的内容会由于优胜劣汰而被系统逐渐过滤掉。这对于平台来说主要是为了内容的更新迭代,使得用户和作者在我们搭建的平台上能自动运转起来,形成良性的循环,从而达到良好的促进和监督作用。
以上讨论了一些工作中常会用到的函数,它们具体的实际应用还需大家去不断地探索发掘,若有发现其他好的函数或应用,也可留言分享出来^_^