基于产生式系统的野人渡河问题求解
人工智能实验
产生式系统(Production system)首先由波斯特(Post)于1943年提出的产生式规则(Production rule)而得名,他们用这种规则对符号串进行置换运算,后来,美国的纽厄尔和西蒙利用这个原理建立了一个人类的认知模型(1965年),同年,斯坦福大学利用产生式系统结构设计出第一个专家系统DENDRAL。
产生式系统用来描述若干个不同的以一个基本概念为基础的系统。这个基本概念就是产生式规则或产生式条件和操作对象的概念。问题描述:用基于产生式系统的方法求解传教士和野人问题
有N个传教士和N个野人来到河边准备渡河,河岸有一条船,每次至多可供K个乘渡,问传教士为了安全起见,应如何规划摆渡方案,使得任何时刻,河岸两边以及船上的野人数目总是不超过传教土的数目,即求解传教士和野人从左岸全部摆渡到右岸的过程中,任何时刻满足M(传教士数)≥C(野人数)和M+C≤K的摆渡方案。
(1) 问题状态的表示
struct status
{
intshipSite=0; //0 stand left, 1 standright ,aim is right
int missionary[2];
intsavage[2];
int step;
};shipSite代表河岸,0代表左岸,1代表目的地右岸。
两个数组missionary和savage分别代表左岸和右岸的传教士或野人人数。
step代表到此状态的步数。
(2) 数据库描述
vector
用一个向量close代表已搜索过的状态,配合这结构体中的step成员,避免在搜索过程中走回头路或这多余搜索。当搜索到的一个新状态存在于close中,则判断当前状态的步数是否小于close中相同状态的步数,若小于,说明该搜索有意义,若不小于,说明该搜索是走了回头路或者无意义的。另外,若新状态不存在于close中,则是新状态,无需判断及进行下一步。
(3) 规则库的描述
bool numberCheck(int &missionary,int&savage)
{
if(savage>missionary &&missionary!=0 )
{
return false;
}
else
{
return true;
}
}规则为,野人数目总是不超过传教土的数目,但同时未明说的还有一条,若传教士在该岸边或者船上的人数为0,则野人的数目在该位置不受影响,用代码表示如上。
(4) 控制机制
bool move(int missionary,int savage,status&nowStatus)
{
nowStatus.missionary[nowStatus.shipSite]-=missionary;
nowStatus.savage[nowStatus.shipSite]-=savage;
nowStatus.shipSite=1-nowStatus.shipSite;
nowStatus.missionary[nowStatus.shipSite]+=missionary;
nowStatus.savage[nowStatus.shipSite]+=savage;
nowStatus.step++;
vector::iterator iter;
iter=find(close.begin(),close.end(),nowStatus);
boolresult1=numberCheck(missionary,savage)&&
numberCheck(nowStatus.missionary[0],nowStatus.savage[0])&&
numberCheck(nowStatus.missionary[1],nowStatus.savage[1]);
boolresult2=false;
if(iter==close.end())
result2=true;
elseif(iter!=close.end()&&iter->step>nowStatus.step)
{
iter->step=nowStatus.step;
result2=true;
}
returnresult1&&result2;} 该函数即为程序中的状态生成函数和控制函数,先是计算出新节点的两岸人数,再对新节点两岸人数和生成该新节点的船上人数进行规则检验,结果与运算存到result1中。
其次对搜索状态进行close数据库检验,如上文所说,若是一个新的有意义节点则为真,结果存到result2中,最终函数返回result1与运算result2。
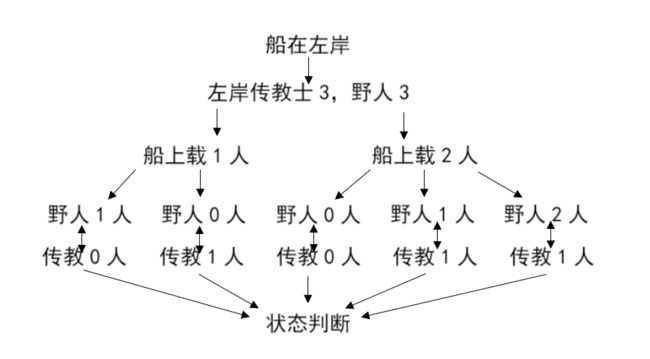
(5) 状态空间图
程序清单
#include
#include
#include
#include
#include
using namespace std;
struct status
{
int shipSite=0; //0 stand left, 1 stand right ,aim is right
int missionary[2];
int savage[2];
int step;
};
int shipMax;
vector close;
bool operator == (const status& obj1,const status& obj2)
{
return
obj1.shipSite==obj2.shipSite&&
obj1.missionary[0]==obj2.missionary[0]&&
obj1.missionary[1]==obj2.missionary[1]&&
obj1.savage[0]==obj2.savage[0]&&
obj1.savage[1]==obj2.savage[1];
}
bool numberCheck(int &missionary,int &savage)
{
if( savage>missionary &&missionary!=0 )
{
return false;
}
else
{
return true;
}
}
bool move(int missionary,int savage,status &nowStatus)
{
nowStatus.missionary[nowStatus.shipSite]-=missionary;
nowStatus.savage[nowStatus.shipSite]-=savage;
nowStatus.shipSite=1-nowStatus.shipSite;
nowStatus.missionary[nowStatus.shipSite]+=missionary;
nowStatus.savage[nowStatus.shipSite]+=savage;
nowStatus.step++;
vector::iterator iter;
iter=find(close.begin(),close.end(),nowStatus);
bool result1=numberCheck(missionary,savage)&&
numberCheck(nowStatus.missionary[0],nowStatus.savage[0])&&
numberCheck(nowStatus.missionary[1],nowStatus.savage[1]);
bool result2=false;
if(iter==close.end())
result2=true;
else if(iter!=close.end()&&iter->step>nowStatus.step)
{
iter->step=nowStatus.step;
result2=true;
}
return result1&&result2;
}
int PruductionSystem(status nowStatus,vector &stepv)
{
if(nowStatus.missionary[0]==0&&nowStatus.savage[0]==0)
{
return nowStatus.step;
}
close.push_back(nowStatus);
int minstep=99999;
vector bufferInsert;
for(int k = 1; k <= shipMax; k++)
{
int shipSavage,shipMissionary;
for(shipSavage = 0; shipSavage <=k,shipSavage<=nowStatus.savage[nowStatus.shipSite]; shipSavage++)
{
//cout< nextStepv;
if(move(shipMissionary,shipSavage,nextStatus))
{
// cout<<"next"<>missionary>>ship;
// savage=missionary;
missionary=3;savage=3;shipMax=2;
// if(2*missionary<=shipMax||shipMax<2)
if( shipMax<2)
{
cout<<"This input illegal"< resultv;
resultv.push_back(start);
int resStep=PruductionSystem(start,resultv);
int i=0;
for(vector::iterator iter=resultv.begin();iter!=resultv.end();iter++)
{
cout<<"Step"<missionary[0]<<" ls"<savage[0]
<<" rm:"<missionary[1]<<" rs"<savage[1]< 主算法采用递归程序设计,每次向子递归传递当前分支探测,并返回是否是可行性结果,用一个close表,来避免探测中的循环以及更新最优路径。