数字图像处理 第三章 灰度转换与空间滤波
3.1 背景
基本灰度转换公式及空间滤波
空间域转换表达式: g ( x , y ) = T [ f ( x , y ) ] g(x, y)=T[f(x, y)] g(x,y)=T[f(x,y)]
3.2 基础的灰度转换公式
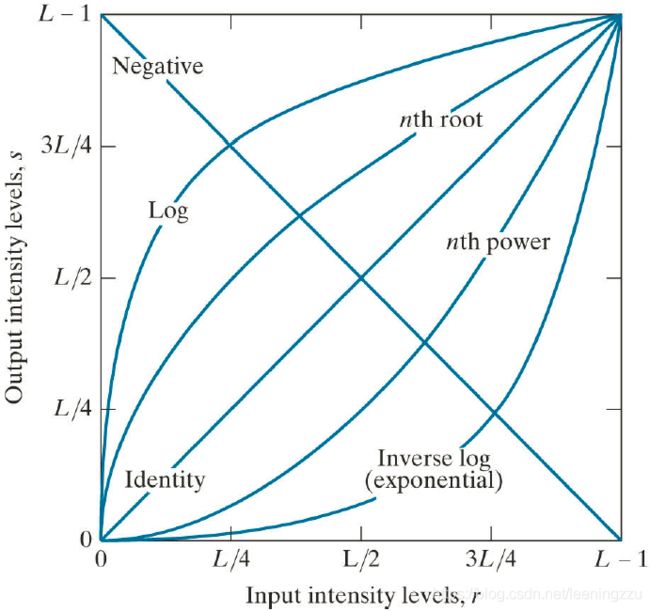
对数转换
s = c log ( 1 + r ) s=c \log (1+r) s=clog(1+r)
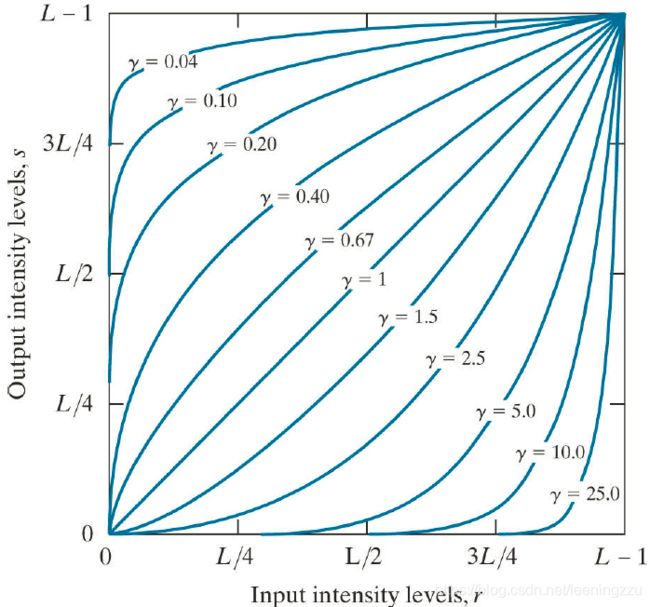
Gamma 转换
s = c r γ s=c r^{\gamma} s=crγ
线性转换
- 对比拉伸
- 灰度级分层
3.3 直方图处理
主要利用微积分面积相等的转换原理对灰度值灰度进行均衡化处理
参考博客:
- 《数字图像处理》–直方图处理
- OpenCV 直方图处理:直方图均衡和规定化(匹配)
3.4 空间滤波基础
空间滤波为一种图像增强方法,其理论基础为空间卷积和空间相关,目的为改善图像质量。
线性空间滤波与频域滤波之间存在着一一对应的关系。
非线性滤波,频域不存在。
滤波,实际上是信号处理中的一个概念,可将图像本身看成是一个二维的信号,其中像素点灰度值的高低代表信号的强弱。
高频:图像中灰度变化剧烈的点,一般是图像轮廓或者是噪声。
低频:图像中平坦的,灰度变化不大的点,图像中的大部分区域。
根据图像的高频与低频的特征,可以设计相应的高通与低通滤波器。高通滤波可以检测图像中尖锐、变化明显的地方;低通滤波可以让图像变得光滑,滤除图像中的噪声。
空间相关和卷积
相关是滤波器模板滑过图像计算每个位置乘积之和的处理,卷积不同点在于滤波器旋转180度。
关于卷积概念可参考:[CV] 通俗理解『卷积』——从傅里叶变换到滤波器和https://zhuanlan.zhihu.com/p/28478034。
空间相关:
( w ☆ f ) ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) (w☆ f)(x, y)=\sum_{s=-a}^{a} \sum_{t=-b}^{b} w(s, t) f(x+s, y+t) (w☆f)(x,y)=s=−a∑at=−b∑bw(s,t)f(x+s,y+t)
卷积:
( w ★ f ) ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x − s , y − t ) (w★ f)(x, y)=\sum_{s=-a}^{a} \sum_{t=-b}^{b} w(s, t) f(x-s, y-t) (w★f)(x,y)=s=−a∑at=−b∑bw(s,t)f(x−s,y−t)
3.5 低通滤波
主要介绍线性的:均值滤波器、高斯滤波器,非线性:中值滤波器。
线性:
- 高斯核大于 ⌈ 6 σ ⌉ × ⌈ 6 σ ⌉ \lceil 6 \sigma\rceil \times\lceil 6 \sigma\rceil ⌈6σ⌉×⌈6σ⌉时,效果差别不大, 与均值滤波器相比,高斯滤波器使边缘更平滑。
- 图像越大(像素点越多),若取得相同效果所需卷积核也越大。
非线性
中值滤波对椒盐噪声效果较好。
3.6 高通滤波
主要通过微分进行边缘增强或灰度变化大的区域,并弱化灰度变换缓慢的区域。
3.6.1 图像微分
一阶微分条件:
(1)在平坦段(灰度不变区域)微分值为零;
(2)在灰度阶梯或斜坡的起始点处微分值非零;
(3)沿着斜坡面微分值非零。
对应于相邻像素间的变化,采用差分进行定义:
∂ f ∂ x = f ( x + 1 ) − f ( x ) \frac{\partial f}{\partial x}=f(x+1)-f(x) ∂x∂f=f(x+1)−f(x)
二阶微分条件:
(1)在平坦去微分值必为零;
(2)在灰度阶梯或斜坡的起始点处微分值非零;
(3)沿着斜坡面微分值非零。
对应于相邻像素间的变化: ∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \frac{\partial^{2} f}{\partial x^{2}}=f(x+1)+f(x-1)-2 f(x) ∂x2∂2f=f(x+1)+f(x−1)−2f(x)
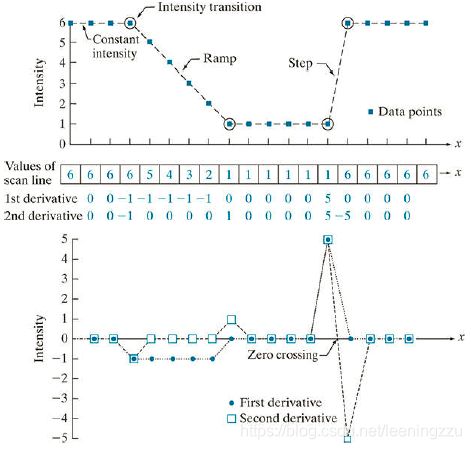
当一阶微分取极值时对应二阶微分为零,图中Zero crossing 即为边缘,二阶微分定位更准确,细节可得到强化。
3.6.2 基于二阶微分的图像增强—拉普拉斯算子
主要构造各向同性滤波器,其响应与图像突变方向无关,具有旋转不变性,即将原始图像旋转后进行滤波处理给出的结果与先对图像滤波,然后再旋转的结果相同。
拉普拉斯为线性算子:
∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^{2} f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} ∇2f=∂x2∂2f+∂y2∂2f
其中 ∂ 2 f ∂ x 2 = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) \frac{\partial^{2} f}{\partial x^{2}}=f(x+1, y)+f(x-1, y)-2 f(x, y) ∂x2∂2f=f(x+1,y)+f(x−1,y)−2f(x,y)
∂ 2 f ∂ y 2 = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) \frac{\partial^{2} f}{\partial y^{2}}=f(x, y+1)+f(x, y-1)-2 f(x, y) ∂y2∂2f=f(x,y+1)+f(x,y−1)−2f(x,y)
则可得 ∇ 2 f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \nabla^{2} f(x, y)=f(x+1, y)+f(x-1, y)+f(x, y+1)+f(x, y-1)-4 f(x, y) ∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
具有旋转不变性的拉普拉斯滤波器:
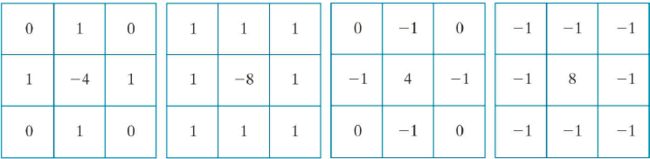
可通过将原始图像与Laplacian叠加来锐化图像:
g ( x , y ) = f ( x , y ) + c [ ∇ 2 f ( x , y ) ] g(x, y)=f(x, y)+c\left[\nabla^{2} f(x, y)\right] g(x,y)=f(x,y)+c[∇2f(x,y)]
3.6.3 非锐化掩模和高提升滤波
步骤
- 模糊原始图像
- 与原始图像做差产生差值图像模板 g mask ( x , y ) = f ( x , y ) − f ‾ ( x , y ) g_{\operatorname{mask}}(x, y)=f(x, y)-\overline{f}(x, y) gmask(x,y)=f(x,y)−f(x,y)
- 将模板与原始图像叠加 g ( x , y ) = f ( x , y ) + k g mask ( x , y ) g(x, y)=f(x, y)+k g_{\operatorname{mask}}(x, y) g(x,y)=f(x,y)+kgmask(x,y).
当 k k k=1时,为非锐化掩模,当>1时为高提升滤波,当<1时减弱模板的作用。注意当 k k k足够大时,可导致边缘出现暗的晕轮,效果反而不好。
3.6.4 一阶微分图像锐化—梯度
梯度
∇ f ≡ grad ( f ) = [ g x g y ] = [ ∂ f ∂ x ∂ f ∂ y ] \nabla f \equiv \operatorname{grad}(f)=\left[\begin{array}{c}{g_{x}} \\ {g_{y}}\end{array}\right]=\left[\begin{array}{c}{\frac{\partial f}{\partial x}} \\ {\frac{\partial f}{\partial y}}\end{array}\right] ∇f≡grad(f)=[gxgy]=[∂x∂f∂y∂f]
其幅度值为 M ( x , y ) = ∥ ∇ f ∥ = mag ( ∇ f ) = g x 2 + g y 2 M(x, y)=\|\nabla f\|=\operatorname{mag}(\nabla f)=\sqrt{g_{x}^{2}+g_{y}^{2}} M(x,y)=∥∇f∥=mag(∇f)=gx2+gy2
其中 M ( x , y ) M(x,y) M(x,y)是与原图像大小相同的图像,该图像通常称为梯度图像。后面的表达式仍保留了灰度的变换,但丢失掉了其各向同性。
主要有一阶Roberts交叉梯度算子和二阶Soble算子
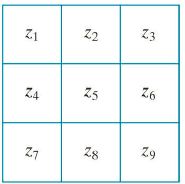
一阶Roberts交叉梯度算子:
g x = ( z 9 − z 5 ) and g y = ( z 8 − z 6 ) g_{x}=\left(z_{9}-z_{5}\right) \quad \text { and } \quad g_{y}=\left(z_{8}-z_{6}\right) gx=(z9−z5) and gy=(z8−z6)
M ( x , y ) = [ ( z 9 − z 5 ) 2 + ( z 8 − z 6 ) 2 ] 1 / 2 M(x, y)=\left[\left(z_{9}-z_{5}\right)^{2}+\left(z_{8}-z_{6}\right)^{2}\right]^{1 / 2} M(x,y)=[(z9−z5)2+(z8−z6)2]1/2
或 M ( x , y ) ≈ ∣ z 9 − z 5 ∣ + ∣ z 8 − z 6 ∣ M(x, y) \approx\left|z_{9}-z_{5}\right|+\left|z_{8}-z_{6}\right| M(x,y)≈∣z9−z5∣+∣z8−z6∣
二阶Soble算子:
g x = ∂ f ∂ x = ( z 7 + 2 z 8 + z 9 ) − ( z 1 + 2 z 2 + z 3 ) g_{x}=\frac{\partial f}{\partial x}=\left(z_{7}+2 z_{8}+z_{9}\right)-\left(z_{1}+2 z_{2}+z_{3}\right) gx=∂x∂f=(z7+2z8+z9)−(z1+2z2+z3)
g y = ∂ f ∂ y = ( z 3 + 2 z 6 + z 9 ) − ( z 1 + 2 z 4 + z 7 ) g_{y}=\frac{\partial f}{\partial y}=\left(z_{3}+2 z_{6}+z_{9}\right)-\left(z_{1}+2 z_{4}+z_{7}\right) gy=∂y∂f=(z3+2z6+z9)−(z1+2z4+z7)
M ( x , y ) = [ g x 2 + g y 2 ] 1 2 = [ [ ( z 7 + 2 z 8 + z 9 ) − ( z 1 + 2 z 2 + z 3 ) ] 2 + [ ( z 3 + 2 z 6 + z 9 ) − ( z 1 + 2 z 4 + z 7 ) ] 2 ] 1 2 \begin{aligned} M(x, y)=\left[g_{x}^{2}+g_{y}^{2}\right]^{\frac{1}{2}}=&\left[\left[\left(z_{7}+2 z_{8}+z_{9}\right)-\left(z_{1}+2 z_{2}+z_{3}\right)\right]^{2}\right.\\ &+\left[\left(z_{3}+2 z_{6}+z_{9}\right)-\left(z_{1}+2 z_{4}+z_{7}\right)\right]^{2} ]^{\frac{1}{2}} \end{aligned} M(x,y)=[gx2+gy2]21=[[(z7+2z8+z9)−(z1+2z2+z3)]2+[(z3+2z6+z9)−(z1+2z4+z7)]2]21
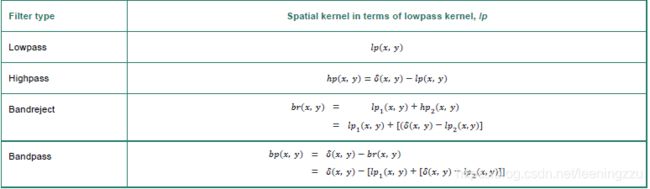
3.7 高通,低通及特定波段滤波
在频域中
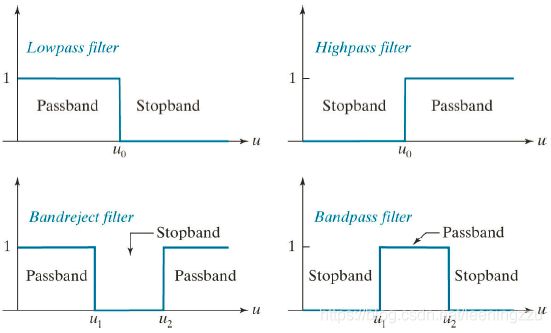
其转换公式为: