最小生成树：kruskal算法的R语言实现

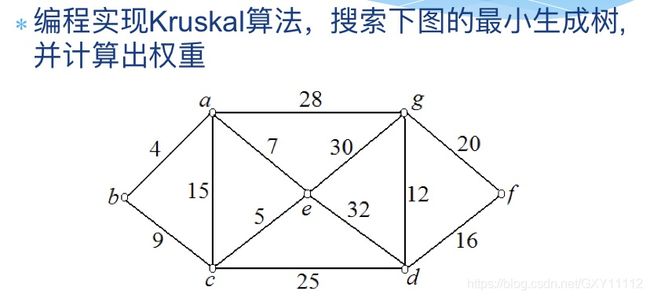
以如下图为例

library(hash)#需要用到hash包
Nodes<-c("A","B","C","D","E","F","G")
#创建存放顶点的向量
edges<- data.frame(start=character(),end=character(),length=numeric(),stringsAsFactors = F)
edges[1,]<-c("A", "B", 4)
edges[10,]<-c("A", "G", 28)
edges[6,]<-c("A", "C", 15)
edges[3,]<-c("A", "E", 7)
edges[4,]<-c("B", "C", 9)
edges[2,]<-c("C", "E", 5)
edges[9,]<-c("C", "D", 25)
edges[12,]<-c("D", "E", 32)
edges[5,]<-c("D", "G", 12)
edges[7,]<-c("D", "F", 16)
edges[11,]<-c("E","G",30)
edges[8,]<-c("F","G",20)
#创建一个edges数据框存放边
edges[,3]<-as.numeric(edges[,3])
ori_trees<-hash()
#创建空哈希,顶点为键——值
for (i in Nodes){
  .set(ori_trees, keys = i, values = i)
}
#将顶点存入哈希中
find_nodes<-function(x){
  if(ori_trees[[x]]!=x){#双亲节点和当前节点不一致，说明这条边添加了minmum spanning tree
    ori_trees[[x]]<-find_nodes(ori_trees[[x]])
    #找到双亲节点未变化的点
    return(ori_trees[[x]])
  }
  else{
    return(x)
  }
}

minimum_spanning_tree<-data.frame(start=character(),end=character(),leng=numeric(),stringsAsFactors = F)
#定义最小生成树
n<-length(Nodes)-1
#定义循环次数，n为需要添加的边数=顶点数-1
s<-0
for(i in 1:dim(edges)[1]){
  if(s==n){
    break
  }
  if(find_nodes(edges[i,1])!=find_nodes(edges[i,2])){
    #双亲节点不一致
    ori_trees[[find_nodes(edges[i,2])]]<-find_nodes(edges[i,1])#改变该顶点的双亲节点
    minimum_spanning_tree<-rbind(minimum_spanning_tree,edges[i,])#将符合条件的边
  s<-s+1
  }
 
}