交叉熵损失函数

(文章同步更新在@dai98.github.io)
交叉熵(Cross Entropy)是与均值误差(MSE)一样常用的损失函数，用在分类中。

一、分类的损失函数

为什么我们选择交叉熵作为损失函数呢？它与其他的损失函数相比有什么好处呢？我们用下面的例子来说明：
我们训练一个简单的神经网络，来判断图片中的动物是猫、狗还是兔子，用独热码表示最后结果。
模型一

正确答案	猫概率	狗概率	兔子概率	预测
猫(1 0 0)	0.8	0.1	0.1	猫(1 0 0)
狗(0 1 0)	0.05	0.9	0.05	狗(0 1 0)
兔子(0 0 1)	0.4	0.3	0.3	猫(1 0 0)

模型二

正确答案	猫概率	狗概率	兔子概率	预测
猫(1 0 0)	0.6	0.2	0.2	猫(1 0 0)
狗(0 1 0)	0.25	0.7	0.05	狗(0 1 0)
兔子(0 0 1)	0.8	0.15	0.05	猫(1 0 0)

我们可以看到，尽管最后两个模型的输出完全一样，但从概率上看，模型一的表现要比模型二更好。

1.分类错误率

最朴素的一种定义方式，是直接计算分类错误的数量占总数量的百分比，即
$$ClassificationError=\frac{numberoferror}{totalnumber}$$上面两个模型的分类错误率都是$\frac{1}{3}$，这样的损失函数无法判断出哪个模型表现更加优异。

2. 均方误差

均方误差一般用于回归，然而它也能用在分类中，我们把每个类别的独热码当作真实值，把概率当作预测值，来计算每个样本的误差，再求平均值，即$$MSE=\frac{1}{n}\sum _{i=1}^n({\hat{y}}_i-y_i{)}^2$$模型一
样本一 $MS{E}_{11}=\frac{1}{3}[(1-0.8{)}^2+(0-0.1{)}^2+(0-0.1{)}^2]=0.02$
样本二 $MS{E}_{12}=\frac{1}{3}[(0-0.05{)}^2+(1-0.95{)}^2+(0-0.05{)}^2]=0.0025$
样本三 $MS{E}_{13}=\frac{1}{3}[(0-0.4{)}^2+(0-0.3{)}^2+(1-0.3{)}^2]=0.247$
模型总误差 $MS{E}_1=\frac{1}{3}(MS{E}_{11}+MS{E}_{12}+MS{E}_{13})=0.0897$
模型二
样本一 $MS{E}_{21}=\frac{1}{3}[(1-0.6{)}^2+(0-0.2{)}^2+(0-0.2{)}^2]=0.08$
样本二 $MS{E}_{22}=\frac{1}{3}[(0-0.25{)}^2+(1-0.7{)}^2+(0-0.05{)}^2]=0.0517$
样本三 $MS{E}_{23}=\frac{1}{3}[(0-0.8{)}^2+(0-0.15{)}^2+(1-0.05{)}^2]=0.5217$
模型总误差 $MS{E}_2=\frac{1}{3}(MS{E}_{21}+MS{E}_{22}+MS{E}_{23})=0.2178$

我们可以看到，由于我们引进对概率的计算，模型一的均方误差要小于模型二的均方误差。然而，我强烈不建议把MSE当作分类的损失函数，有以下两个原因：一是MSE用作分类的时候，训练刚开始的时候梯度下降的速度非常缓慢；二是并不是所有分类模型的MSE都是凸问题，因此深度学习的优化器表现会非常糟糕。下面我们来介绍比MSE在分类中更好用的交叉熵。
 

二、交叉熵的推导

交叉熵是信息论中的内容，我们从最基础的概念开始推导。

1. 信息量

一件事情可以包含多少信息呢？显而易见的事情大家都明白，不会包含很多信息；相反，出现概率越小的事情，就越违背人的直觉，也包含了越多的信息。例如：期中考试以往班上的第一名考了第一名，这件事在常人看来是正常的；而班级的最后一名考了第一名，蕴含了许多的信息——或许是他十分努力，奋发图强，或是他在课外和补习班老师上课，等等，都作为隐藏的信息，包含在这个事件当中。因此我们发现，一件事情的信息量与其发生的概率有关。
我们设离散随机变量$X$为事件，$\chi$为其取值范围，$p(x)=Pr(X=x),x\in \chi$为事件$x$发生的概率，我们定义$X=x_0$的信息量为(注：所有对数的底都是自然对数$e$):$$I(x_0)=-\log (p(x_0))$$

2.信息熵

为什么我们要为事件$X$定义一个取值范围呢？因为一件事情可能有各种各样的可能性，而$\chi$代表了事件发生所有的可能性。例如：我打开了电脑，

事件	概率
电脑正常开机	0.95
电脑黑屏，无法启动	0.04
电脑爆炸了	0.01

信息熵的定义是，所有事件的信息量乘上概率的期望，即
$$H(X)=-\sum _{i=1}^{n}p(x_i)\log (p(x_i))$$在上面的例子中，我们的信息熵为$H(X)=-(0.95\times \log (0.95)+0.05\times \log (0.05)+0.01\times \log (0.01))$。
有的问题只有两个可能性（例如扔硬币），服从伯努利分布，可以将信息熵的公式简化为：
设$p(0)=p,p(1)=1-p$
$$\begin{array}{rl}H(X)& =-\sum _{i=1}^{n}p(x_i)\log (p(x_i))\\ & =-(p\log p+(1-p)\log (1-p))\\ & =-p\log p-(1-p)\log (1-p)\end{array}$$

3. 相对熵/KL散度

不同事件在不同的条件下发生的概率是不同的，比如夏天和冬天买雪糕的概率是不同的。假设对于一个事件$X$，有两个概率分布$P(X)$和$Q(X)$。KL散度(Kullback-Leibler Divergence)指的就是在两个不同的概率分布下，该事件的信息熵的增量是多少。
在机器学习中，$P(X)$通常指代数据的真实分布，比如$[100]$，我们也可以将其理解为概率，因为已经是真实发生的数据了，所以我们非常肯定因变量属于哪一个类型，可以给对应的类型1的概率。$Q(X)$通常指代的是我们的预测结果，比如$[0.70.20.1]$，我们可以发现，我们的预测值不像真实值一样确定，所以我们需要更多的训练，来获取信息增量，才能让$Q(X)$到达$P(X)$的水平，当我们经过反复的训练，让Q变得和P一样完美，不再需要额外的信息增量了，此时Q与P等价；由此我们可以推导出KL散度的公式：
$$\begin{array}{rl}{D}_{KL}(p||q)& =\sum _{i=1}^{n}p(x_i)\log (\frac{p(x_i)}{q(x_i)})\\ & =\sum _{i=1}^{n}p(x_i)\log (p(x_i))-\sum _{i=1}^{n}p(x_i)\log (q(x_i))\end{array}$$由此我们发现，KL散度越小，$P$分布和$Q$分布越接近。

4. 交叉熵

我们在KL散度的公式的基础上继续推导：
$$\begin{array}{rl}{D}_{KL}(p||q)& =\sum _{i=1}^{n}p(x_i)\log (p(x_i))-\sum _{i=1}^{n}p(x_i)\log (q(x_i))\\ & =-H(p(X))+[-\sum _{i=1}^{n}p(x_i)\log (q(x_i))]\end{array}$$因为前面就是p的信息熵，是一个常数，我们把后面的部分定义为交叉熵：
$$H(p,q)=-\sum _{i=1}^{n}p(x_i)\log (q(x_i))$$在机器学习中，我们需要评估预测值与标签的差距，用的交叉熵当作损失函数，即$D_{KL}(y||\hat{y})$。

5. 交叉熵的计算

我们来计算一算上文两个模型的交叉熵分别是多少：
模型一
样本一 $H(y,\hat{y}{)}_{11}=-[1\times \log 0.8+0\times \log 0.1+0\times \log 0.1]=0.2231$
样本二 $H(y,\hat{y}{)}_{12}=-[0\times \log 0.05+1\times \log 0.9+0\times \log 0.05]=0.1054$
样本三 $H(y,\hat{y}{)}_{13}=-[0\times \log 0.4+0\times \log 0.3+1\times \log 0.3]=1.204$
模型总误差 $H(y,\hat{y}{)}_1=\frac{1}{3}(H(y,\hat{y}{)}_{11}+H(y,\hat{y}{)}_{12}+H(y,\hat{y}{)}_{13})=0.511$
模型二
样本一 $H(y,\hat{y}{)}_{21}=-[1\times \log 0.6+0\times \log 0.2+0\times \log 0.2]=0.5108$
样本二 $H(y,\hat{y}{)}_{22}=-[0\times \log 0.25+1\times \log 0.7+0\times \log 0.05]=0.3567$
样本三 $H(y,\hat{y}{)}_{23}=-[0\times \log 0.8+0\times \log 0.15+1\times \log 0.05]=2.9957$
模型总误差 $H(y,\hat{y}{)}_2=\frac{1}{3}(H(y,\hat{y}{)}_{21}+H(y,\hat{y}{)}_{22}+H(y,\hat{y}{)}_{23})=1.288$
 
可以看到，交叉熵可以捕获两个模型之间的差距。
 

三、反向传播

我们来看看模型最后两层的反向传播的情况。由于二分类和多分类我们使用的激活函数不同，因此我们需要单独对其进行求导。

1. 二分类

二分类的模型最后一层的激活函数使用的是Sigmoid函数，我们来看一下模型的结构：

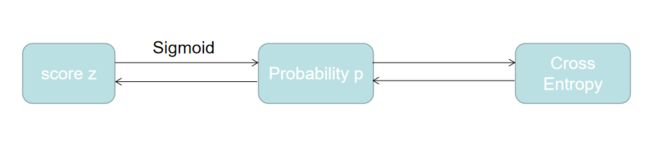
根据链式法则，
$$\frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial p}\cdot \frac{\partial p}{\partial z}\cdot \frac{\partial z}{\partial w_i}$$我们依次进行求导
$$\begin{array}{rl}\frac{\partial L}{\partial p}& =\frac{\partial }{\partial p}[-(y\log p+(1-y)\log (1-p))]\\ & =-\frac{y}{p}+\frac{1-y}{1-p}\end{array}$$
$$\begin{array}{rl}\frac{\partial p}{\partial z}& =\frac{\partial \sigma (z)}{\partial z}=\frac{\partial }{\partial z}(\frac{e^z}{1+e^z})\\ & =\frac{\partial }{\partial z}(\frac{1}{1+e^{-z}})\\ & =\frac{e^{-z}}{(1+e^{-z}{)}^2}\\ & =\frac{1}{1+e^{-z}}\times \frac{e^{-z}}{1+e^{-z}}\\ & =\sigma (z)\cdot [1-\sigma (z)]\end{array}$$
$$\begin{array}{r}\frac{\partial z}{\partial w_i}=\frac{\partial }{\partial w_i}(w_i{x}_i+b_i)=x_i\end{array}$$
$$\begin{array}{rl}\frac{\partial L}{\partial w_i}& =\frac{\partial L}{\partial p}\cdot \frac{\partial p}{\partial z}\cdot \frac{\partial z}{\partial w_i}\\ & =[-\frac{y}{p}+\frac{1-y}{1-p}]\cdot \sigma (z)\cdot [1-\sigma (z)]\cdot x_i\\ & =[-\frac{y}{\sigma (z)}+\frac{1-y}{1-\sigma (z)}]\cdot \sigma (z)\cdot [1-\sigma (z)]\cdot x_i\\ & =[-y[1-\sigma (z)]+(1-y)\sigma (z)]\cdot x_i\\ & =[-y+y\cdot \sigma (z)+\sigma (z)-y\cdot \sigma (z)]\cdot x_i\\ & =[\sigma (z)-y]\cdot x_i\end{array}$$

2.多分类

多分类模型最后一层的激活函数使用的是Softmax函数，模型结构为：

和上面一样，根据链式法则，
$$\frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial p}\cdot \frac{\partial p}{\partial z}\cdot \frac{\partial z}{\partial w_i}$$我们依次进行求导
$$\begin{array}{rl}\frac{\partial L}{\partial p}& =\frac{\partial }{\partial p}[-\sum _{i=1}^n{y}_i\log p]\\ & =-\sum _{i=1}^n\frac{y_i}{p}\end{array}$$
Softmax函数的公式为$\sigma (z_i)=\frac{e^{z_i}}{{\sum }_{k=1}^n{e}^{z_k}}$，然而，Softmax在计算的过程中经常出现由于数据溢出导致的返回nan的情况，因此我们需要将其乘上一个系数，让数值大小下降下来，即：
$$\begin{array}{rl}\sigma (z_i)& =\frac{C{e}^{z_i}}{C{\sum }_{k=1}^n{e}^{z_k}}\\ & =\frac{e^{z_i+\log C}}{{\sum }_{k=1}^n{e}^{z_k+\log C}}\end{array}$$
我们通常让$\log C=-\max (z)$，让比较大的指数变小；由此，我们设$z_i-\log C=z_i^{\prime }$，并求其梯度
$$\begin{array}{rl}\frac{\partial p}{\partial z_j^{\prime }}& =\frac{\partial \sigma (z_i^{\prime })}{\partial z_j^{\prime }}=\frac{\partial }{\partial z_j^{\prime }}\frac{e^{z_i^{\prime }}}{{\sum }_{k=1}^n{e}^{z_k^{\prime }}}\end{array}$$
当$i\ne j$时
$$\begin{array}{rl}\frac{\partial p}{\partial z_j^{\prime }}& =\frac{0-e^{z_i^{\prime }}{e}^{z_j^{\prime }}}{({\sum }_{k=1}^n{e}^{z_k^{\prime }}{)}^2}\\ & =-\frac{e^{z_i^{\prime }}}{({\sum }_{k=1}^n{e}^{z_k^{\prime }})}\cdot \frac{e^{z_j^{\prime }}}{({\sum }_{k=1}^n{e}^{z_k^{\prime }})}\\ & =-\sigma (z_i)\cdot \sigma (z_j)\end{array}$$
当$i=j$时
$$\begin{array}{rl}\frac{\partial p}{\partial z_j^{\prime }}& =\frac{e^{z_i^{\prime }}{\sum }_{k=1}^n{e}^{z_k^{\prime }}-(e^{z_i^{\prime }}{)}^2}{({\sum }_{k=1}^n{e}^{z_k^{\prime }}{)}^2}\\ & =\frac{e^{z_i^{\prime }}}{({\sum }_{k=1}^n{e}^{z_k^{\prime }})}\cdot \frac{{\sum }_{k=1}^n{e}^{z_k^{\prime }}-e^{z_i^{\prime }}}{({\sum }_{k=1}^n{e}^{z_k^{\prime }})}\\ & =\sigma (z_i^{\prime })\cdot (1-\sigma (z_j^{\prime }))\end{array}$$
由此可得：
$$\frac{\partial p}{\partial z_j^{\prime }}=\{\begin{array}{ll}-\sigma (z_i)\cdot \sigma (z_j),& i\ne j\\ \sigma (z_i)\cdot (1-\sigma (z_j)),& i=j\end{array}$$
$$\begin{array}{r}\frac{\partial z}{\partial w_i}=\frac{\partial }{\partial w_i}(w_i{x}_i+b_i)=x_i\end{array}$$
$$\begin{array}{rl}\frac{\partial L}{\partial w_i}& =\frac{\partial L}{\partial p}\cdot \frac{\partial p}{\partial z}\cdot \frac{\partial z}{\partial w_i}\\ & =-[\sum _{k\ne i}^n\frac{y_k}{p_k}\cdot [-\sigma (z_i)\cdot \sigma (z_k)]+\frac{y_i}{p_i}\cdot \sigma (z_i)\cdot (1-\sigma (z_i))]\cdot x_i\\ & =-[\sum _{k\ne i}^n\frac{y_k}{\sigma (z_k)}\cdot [-\sigma (z_i)\cdot \sigma (z_k)]+\frac{y_i}{\sigma (z_i)}\cdot \sigma (z_i)\cdot (1-\sigma (z_i))]\cdot x_i\\ & =-[-\sum _{k\ne i}^n{y}_k\cdot \sigma (z_i)+y_i(1-\sigma (z_i))]\cdot x_i\\ & =[\sum _{k\ne i}^n{y}_k\cdot \sigma (z_i)+y_i\cdot \sigma (z_i)-y_i]\cdot x_i\end{array}$$
因为我们的向量$y$是独热码表示，所以${\sum }_{k\ne i}^n{y}_k+y_i=1$，因此上式可以化简为：
$$\frac{\partial L}{\partial w_i}=[\sigma (z_i)-y_i]\cdot x_i$$
 

四、交叉熵的实现

import numpy as np


class Loss:
	def loss(self, predicted:Tensor, actual:Tensor) -> Tensor:
		raise NotImplementedError
	def grad(self, predicted:Tensor, actual:Tensor) -> Tensor:
		raise NotImplementedError


class CrossEntropy(Loss):
	def loss(self, predicted:Tensor, actual:Tensor) -> Tensor:
		m = actual.shape[0]
		log_likelihood = -np.log(predicted)
		loss = np.sum(log_likelihood) / m
		return loss

	def grad(self, predicted:Tensor, actual:Tensor) -> Tensor:
		m = actual.shape[0]
		grad = predicted[range(m),actual.tolist()] - 1
		grad /= m
		return grad
		

 

五、参考资料

[1]. 知乎专栏：损失函数 - 交叉熵损失函数
[2]. 一文搞懂交叉熵在机器学习中的应用，透彻理解交叉熵背后的直觉
[3]. Softmax和交叉熵的深度解析和Python实现
[4]. Stanford University CS230 - Deep Learning