计算几何 学习笔记

基础知识

基本操作

基本定义

struct dot {
	double x, y;
	dot(double _x, double _y) {x = _x, y = _y;}
	dot() {}
};

struct line {
	dot p, v;
	line(dot _p, dot _v) {p = _p, v = _v;}
	line() {}
};

double dcmp(double x) {
	if (fabs(x) < eps) return 0; else return (x < 0 ? -1 : 1);
}

dot operator + (dot a, dot b) {return dot(a.x + b.x, a.y + b.y);}
dot operator - (dot a, dot b) {return dot(a.x - b.x, a.y - b.y);}
dot operator * (dot a, double b) {return dot(a.x * b, a.y * b);}

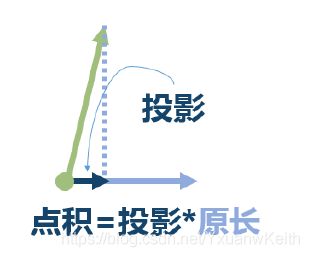
点积

表示向量$u$在向量$v$上的投影的模长乘以向量$v$模长。

1. 点积基本运算

double dot(dot a, dot b) {return a.x * b.x + a.y * b.y;}

2. 向量模长

double len(dot a) {return sqrt(dot(a, a));}

3. 调整向量长度

dot adjust(dot a, double b) {return a * (b / len(a));}

4. 投影长度

double shade(dot a, dot b) {return dot(a, b) / len(a);}

叉积

表示两个向量为邻边构成的平行四边形的有向面积。

叉积表示的为有向面积，其定义为：一个向量与一个位于其左手的向量的叉积为正，而与其右手的向量叉积为负。

1. 叉积基本运算

double cro(dot a, dot b) {return a.x * b.y - a.y * b.x;}

2. 判断向量b位于向量a的方向，左手为0，右手为1

bool direct(dot a, dot b) {return cro(a, b) <= 0;}

其他基本操作

1. 返回一个向量的垂直向量

dot perpendicular(dot a) {return dot(a.y, -a.x);}

2. 返回两个点之间的距离

double dist(dot a, dot b) {return len(a - b);}

3. 点到直线距离
   利用点与直线上两点构成的平行四边形，用面积除以底边长得到高，也就是距离。
   

double listl(line a, dot b) {return fabs(cro(b - a.p, a.v) / len(a.v));}

快速排斥实验

判断两条直线有没有交点需要通过快速排斥实验和跨立实验

快速排斥实验

判断以两条直线为对角线的矩形是否相交，如果不相交则线段不可能相交；如果矩形相交则进行跨立实验

跨立实验

判断线段A的两个端点是否分别位于直线B的两侧；线段B的两个端点是否位于直线A的两侧。如果在同侧则无交点，使用叉积判断一个点在直线的哪一侧。

bool repel(dot a, dot b, dot c, dot d) {
	if (min(a.x, b.x) > max(c.x, d.x) || min(a.y, b.y) > max(c.y, d.y) || min(c.x, d.x) > max(a.x, b.x) || min(c.y, d.y) > max(a.y, b.y)) return 0;
	return 1;
}

bool straddle(dot a, dot b, dot c, dot d) {
	return ((dcmp(cro(a - b, c - b)) * dcmp(cro(a - b, d - b)) <= 0) && 
	(dcmp(cro(c - d, a - d)) * dcmp(cro(c - d, b - d))) <= 0);
}

bool LineCross(line a, line b) {
	dot A = a.p, B = a.p + a.v, C = b.p, D = b.p + b.v;
	if (!repel(A, B, C, D)) return 0;
	return straddle(A, B, C, D);
}

两直线求交点

如图，我们需要求解直线$A$与直线$B$的交点$P$，令
$$\begin{gathered} A.q=A.p+A.v \\ B.q=B.p+B.v \end{gathered}$$
如果计算出$\overline{B.pB.q}$与$\overline{B.pP}$的比值，就可以利用比例关系计算出点$P$。从图中可以看出，两者的比值等一$H2$与$H1$的比值，又等于$S2$与$S1$的比值。而$S1,S2$可以通过叉积的计算得到。

dot intersect(line a, line b) {
	return b.p + b.v * (cro(a.v, a.p - b.p) / cro(a.v, b.v));
}

判断点是否在线段上

判断点$p$是否在线段上$a$时，首先判断是否在线段$a$所处的直线上，然后再判断是否在两个端点之间即可。

bool OnSegment(line a, dot p) {
	dot A = a.p, B = a.p + a.v;
	return dcmp(cro(A - p, B - p)) == 0 && dcmp((A - p) * (B - p)) < 0;
}