7/13数字图像处理笔记

频率域滤波

滤波器：抑制或最小化某些频率的波或振荡的装置或材料
频率：自变量单位变化期间，一个周期函数重复相同值序列的次数

基本概念

傅里叶级数

傅里叶级数：具有周期T的连续变量t的函数f(t)可被描述为乘以适当系数的正弦和/或余弦和

其中

傅里叶变换

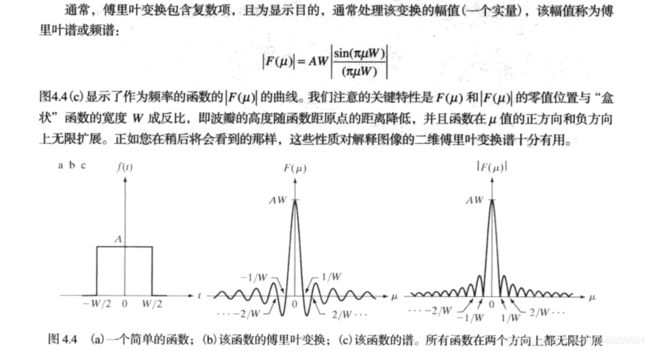
傅里叶变换：非周期函数（该曲线下面积有限）可以用正弦和/或余弦乘以加权函数的积分表示连续变量t的连续函数f(t)的傅里叶变换定义如下。因为t积分过了，F(μ)仅是μ的函数

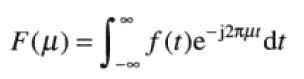
傅里叶反变换：函数可由其傅里叶变换恢复

用傅里叶级数/变换表示的函数特征可以用傅里叶反变换来重建，不会丢失任何信息

冲激及其取样特征

连续变量t在t=0处的单位冲激为δ(t)，定义如下，且满足第二个式子。物理上把t看成时间，则一个冲激可理解为幅度无限、持续时间为0，拥有单位面积的尖峰信号。


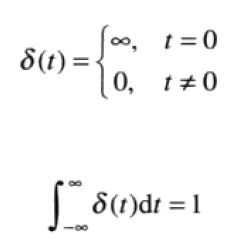
一个冲激具有取样特性，取样特性得到函数在冲激位置的值


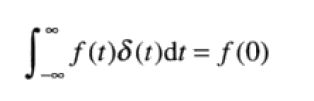
位于任意点t0的冲激表示为δ(t−t0)，取样特性在冲激位置t0处得到函数值

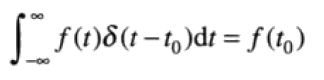
离散形式

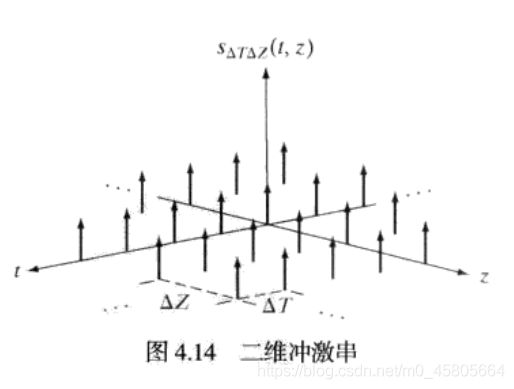
冲激串：无线多个分离的周期冲激单元ΔT之和

卷积

已经知道两个函数的卷积涉及一个函数关于原点做翻转（旋转180度）并滑过另一个函数。
连续变量t的两个连续函数f(t)，h(t)的卷积必须用积分代替求和：

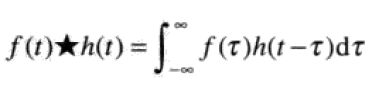
负号表示翻转，t是一个函数滑过另一个函数的位移
空间域中两个函数的卷积的傅里叶变换=两个函数的傅里叶变换在频率域中的乘积。如果有两个变换的乘积，即可通过计算傅里叶反变换得到空间域的乘积

取样和取样函数的傅里叶变换

取样

计算机处理之前，连续函数必须转换为离散值序列，通过取样和量化来完成。对一个连续函数f(t)，以独立变量t的均匀间隔ΔT取样，用一个ΔT单位间隔的冲激串作为取样函数乘以f(t)。
取样后的函数：

序列中任取样值fk:

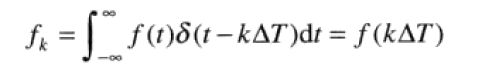
取样函数的傅里叶变换

下式为冲激串的傅里叶变换

F(μ)和S(μ)的卷积为：

取样后的函数的傅里叶变换是F(μ)的一个拷贝的无限周期序列，是原始函数的傅里叶变换。

取样定理

如果从取样函数的傅里叶变换中包含的这个函数的拷贝的周期序列中分离出F(μ)的一个拷贝，且拷贝间的间距足够，则从取样函数的傅里叶变换中提取一个单周期使其等于F(μ)是可能的

满足上式即可保证有足够大的间距
以上公式说明如果以超过函数最高频率的两倍的取样率来获得样本，连续函数的带限函数可以完全从它的样本集恢复

一个带限函数使用频率域方法由其样本复原（从取样函数的傅里叶变换中恢复）

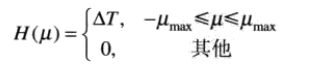
通过H(μ)和F˜(μ)相乘得到F(μ)

利用傅里叶反变换复原f(t)

混淆

如果一个带限函数用低于其最高频率的两倍取样率取样会发生欠取样，最终效果是周期重叠，且不管使用什么滤波器，都不可能分离出变量的一个单周期。这将使得我们无法知道这些样本是不是原始函数的真实描述。这个现象叫做频率混淆，简称混淆
可以通过平滑输入函数减少高频分量的方法（如对图像采用散焦）来降低混淆的影响，这种处理称为抗混淆，必须在函数被取样之前完成

由取样后的数据重建函数

使用卷积定理：



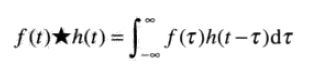
将取样后的函数f˜(t)代入上式，使用下面的卷积公式
可导出f(t)的空间域表达式：

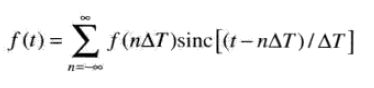
单变量的离散傅里叶变换(DFT)

由取样后的函数的连续变换得到DFT

对一个周期采样是DFT的基础
将取样后函数代替傅里叶反变换公式中的f(t)，得到

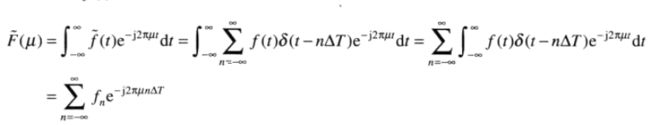
在如下频率处取样得到在周期μ=0到μ=1/ΔT之间得到F˜(μ)
的M个等间距样本 ：

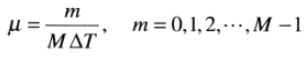
代入上式得到离散傅里叶变换：

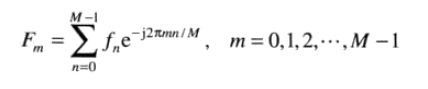
可以用傅里叶反变换复原样本集fn

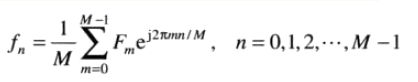
离散傅里叶变换对适用于任何均匀取样的有限离散样本集

取样和频率间隔之间的关系

离散频率域中的相应间隔（DFT的频率分辨率）Δμ取决于连续函数f(t)被取样的持续时间T，且DFT跨越的频率范围取决于取样间隔

两个变量的函数的拓展

二维冲激及其取样特性

两个连续变量t和z的的冲激定义为：

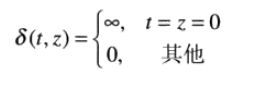
二维冲激在积分下的取样特性：


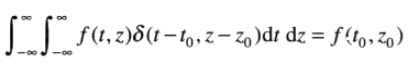
对于离散变量x，y，二维离散冲激为：

取样特性：

二维连续傅里叶变换对

二维取样和取样定理

如果取样率满足

则连续带限函数可以由其一组样本无误地恢复

图像中的混淆

图像混淆
图像中主要存在空间混淆和时间混淆。前者由欠取样造成，后者与图像序列中图像间的时间间隔有关
重点关注空间混淆。主要表现形式是人为引入的缺陷。通过稍微散焦被数字化的场景来削弱高频可以降低混淆的影响。

图像内插和重取样
图像处理中二维内插最普通的应用：调整图像大小。放大可看成是过取样，缩小可看成欠取样

莫尔（波纹）模式
一种人为缺陷，指在两个近似等间隔的光栅之间产生的差拍模式，有时是使用周期或近似周期分量对场景取样产生的

二维离散傅里叶变换及其反变换

二维离散傅里叶变换的性质

空间和频率间隔的关系

假设对连续函数f(t,z)取样生成了一副数字图像f(x,y)，令ΔT\Delta TΔT和ΔZ\Delta ZΔZ表示样本间的间隔，则相应离散频率域变量间的间隔分别由以下两个式子给出。频率域样本间的间隔与空间样本间的间距和样本数成反比

平移和旋转

傅里叶变换对满足平移特性

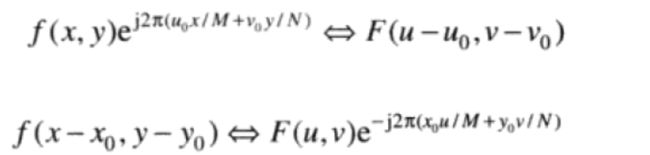
用指数项乘以f(x,y)将使得DFT的原点移到点(u0,v0)，反之，用负指数乘以F(u,v)将使得f(x,y)的原点移到点(x0,y0)

周期性

在区间[0,M-1]中，变换数据由两个在点M/2处碰面的背靠背的半个周期组成

对称性

任意实函数或虚函数可表示为一个奇数部分和一个偶数部分的和

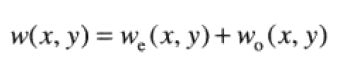
偶数和奇数部分定义如下：

由前面的定义有：

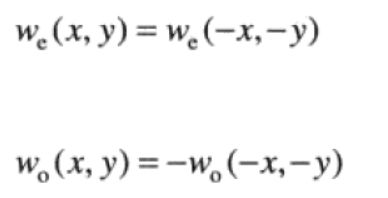
即偶函数是对称的， 奇函数是反对称的。DFT和IDFT中所有指数都是正的，谈论对称(反对称)时，指的是关于序列中点的对称(反对称)。仅考虑非负指数项，奇偶定义变为


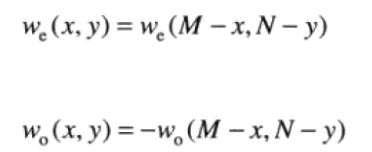
对称性质：

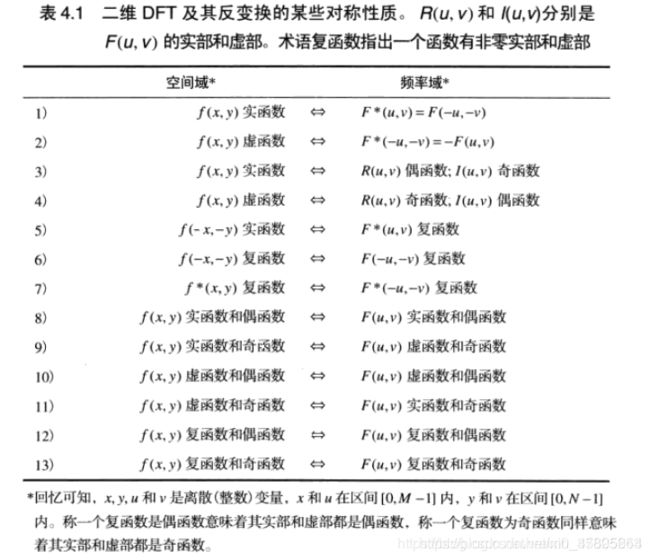
如性质3：如果f(x,y)是实函数，则其DFT的实部是偶函数，虚部是奇函数；如果一个DFT分别具有偶函数的实部和奇函数的虚部，则其IDFT是一个实数

傅里叶谱和相角

二维DFT一般是复函数，可用极坐标形式表示

它的幅度被称为傅里叶谱（频谱）

下式被称为相角

功率谱定义为

实函数的傅里叶变换是共轭对称的，谱是关于原点欧对称的，相角关于原点及对称


F(0,0)是谱的最大分量，有时被称为变换的直流分量

如果f(x,y)是虚函数，则其傅里叶变换是共轭反对称的：F∗(−u,−v)=F(u,v)
简单函数的二维傅里叶谱

二维卷积定理

二维循环卷积：

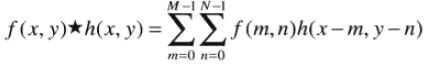
二维卷积定理：


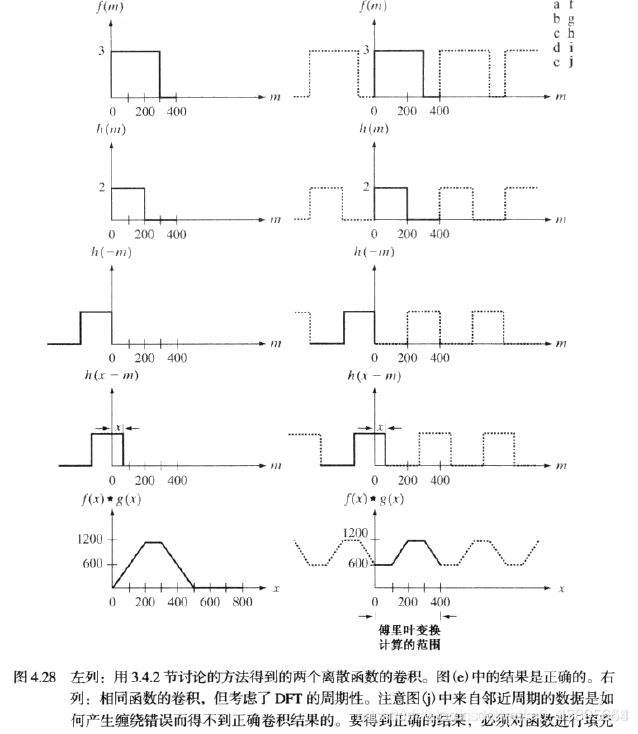
缠绕错误：分别有A个样本和B个样本的两个周期函数的卷积的周期的靠近使它们互相干扰
解决：0填充，使它们具有相同长度P

频率域滤波

频率域滤波由修改一幅图像的傅里叶变换然后计算其反变换得到处理后的结果组成

滤波函数修改输入图像的变换来得到处理后额输出g(x,y)
频率域滤波步骤

空间和频率域滤波间的对应

空间域和频率域滤波间的纽带是卷积定理

给定一个滤波器H(u,v)，要找出其空间域的等价表示。滤波后的输出是 ，这是频率域滤波器的反变换，对应于空间域的滤波器。反过来，根据卷积定理，给定一个空间滤波器，可以用其傅里叶变换得到其频率域表示。两个滤波器形成了傅里叶变换对，

其中h(x,y)是一个空间滤波器。因为该滤波器可以由频率域滤波器对一个冲激的响应得到，所以h称为H的脉冲响应。这样的滤波器称为有限冲激响应滤波器，是一类线性空间滤波器
一维频率域高斯滤波器

更复杂的滤波器可以用基本高斯函数构建

使用频率域滤波器平滑图像

在频率域平滑可通过对高斯的衰减达到，也就是用低通滤波
三类低通滤波器：涵盖从非常尖锐（理想）到非常平滑（高斯）的滤波范围
理想滤波器ILPF

关于原点径向对称。“理想”表明在半径为D0的圆内，所有频率无衰减通过，圆外所有频率完全被衰减（滤除）

布特沃斯滤波器
两种滤波器的过渡。阶数值较高时，该滤波器接近于理想滤波器，较低时更像高斯滤波器

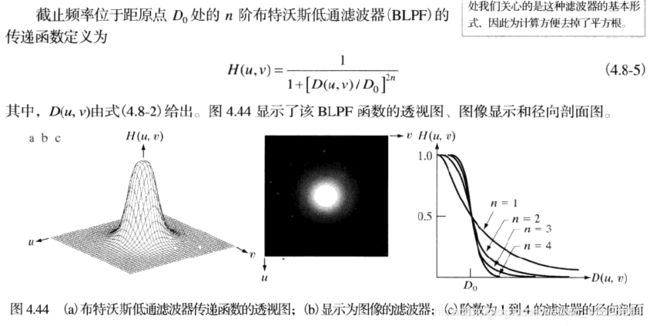
高斯滤波器

使用频率域滤波器锐化图像

因为边缘和其他灰度的急剧变化与高频分量有关，所以图像的锐化可在频率域通过高通滤波来实现，高通滤波会衰减傅里叶变换中的低频分量而不会扰乱高频信息

理想高通滤波器IHPF

IHPF将半径为D0的圆内的所有频率置零，毫无衰减地通过圆外所有频率

布特沃斯高通滤波器

高斯高通滤波器

频率域的拉普拉斯算子

拉普拉斯算子可使用如下滤波器在频率域实现：

或者关于频率矩形的中心，使用如下滤波器：

钝化模板、高提升滤波和高频强调滤波

使用频率域方法，钝化模板：

同态滤波

照射-反射模型可用于开发一种频率域处理过程，通过同时压缩灰度范围和增强对比度来改善图像表现
一幅图像f(x,y)可表示为照射分量i和反射分量r的乘积

定义

则有

F分别是对ln i(x,y)或ln r(x,y)的傅里叶变换

同态滤波函数H分别对照射分量和反射分量进行操作

选择性滤波

处理指定的频段或频率矩形的小区域

带阻滤波器、带通滤波器

陷波滤波器

拒绝或通过实现定义的关于频率矩形中心的一个邻域的频率。可用中心已被平移到陷波滤波器中心的高通滤波器的乘积构造

可减少莫尔模式