鸽鸽

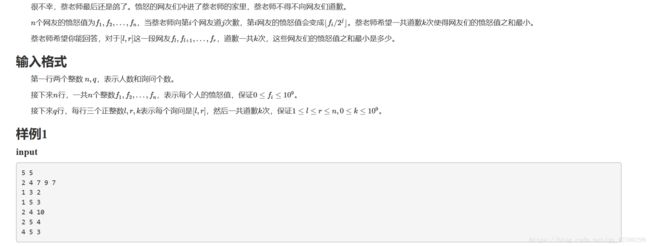
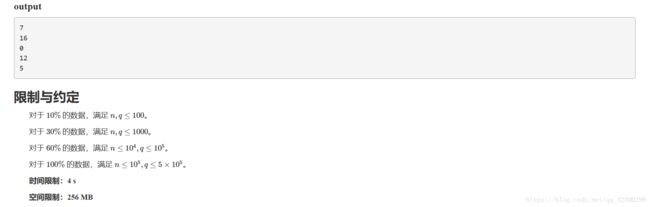
对每个人求出第1次，第2次，第3次…道歉的贡献
对于一个区间，先选贡献最大的那些道歉。
然后变成了一个区间前k大和的问题，需要用主席树。

席树的主体就是线段树，准确的说，就是很多棵线段树，存的是一段数字区间出现次数（所以要先离散化可能出现的数字）。举个例子，假设我每次都要求整个序列内的第 k 小，那么对整个序列构造一个线段树，然后在线段树上不断找第 k 小在当前数字区间的左半部分还是右半部分。这个操作和平衡树的 Rank 操作一样，只是这里将离散的数字搞成了连续的数字。

这道题我当时的思路是贪心。
求出如果我个当前这个人道歉能让他减多少愤怒值
每次给减去愤怒值最多的人道歉
时间复杂度太高

#include
typedef long long ll;
using namespace std;
const int N=5e5+7;
struct node
{
 int lc,rc,sz;
 ll sum;
}t[N*20];
struct query
{
 int l,r,k;
}q[N];
int n,m,tot,a[N],rt[N];
ll s[N],sum[N],sz[N],ans[N];
void insert(int prt,int&rt,int l,int r,int k)
{
 rt=++tot,t[rt]=t[prt],t[rt].sz++,t[rt].sum+=k;
 if(l==r)
  return;
 int mid=(l+r)/2;
 if(k<=mid)
  insert(t[prt].lc,t[rt].lc,l,mid,k);
 else 
  insert(t[prt].rc,t[rt].rc,mid+1,r,k);
}
ll query(int L,int R,int l,int r,int k)
{
 if(l==r)
  return 1ll*k*l;
 int mid=(l+r)/2,tmp=t[t[R].rc].sz-t[t[L].rc].sz;
 if(tmp>=k)
  return query(t[L].rc,t[R].rc,mid+1,r,k);
 return t[t[R].rc].sum-t[t[L].rc].sum+query(t[L].lc,t[R].lc,l,mid,k-tmp);
}
int main()
{
 scanf("%d%d",&n,&m);
 for(int i=1;i<=n;i++)
  scanf("%d",&a[i]),s[i]=s[i-1]+a[i];
 for(int i=1;i<=m;i++)
  scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].k);
 for(int bit=1<<30;~bit;bit>>=1)
 {
  memset(rt,0,sizeof rt);
  tot=0;
  for(int i=1;i<=n;i++)
  {
   rt[i]=rt[i-1];
   sum[i]=sum[i-1];
   sz[i]=sz[i-1];
   if(a[i]-a[i]/2>=max(bit,1))
    insert(rt[i],rt[i],1,1e9,a[i]-a[i]/2),sum[i]+=a[i]-a[i]/2,sz[i]++,a[i]/=2;
  }
  for(int i=1;i<=m;i++)
  {
   int l=q[i].l-1,r=q[i].r,k=q[i].k;
   if(!k||sz[q[i].r]-sz[l]==0)
    continue;
   if(sz[r]-sz[l]<=k)
    ans[i]+=sum[r]-sum[l],q[i].k-=sz[r]-sz[l];
   else 
    ans[i]+=query(rt[l],rt[r],1,1e9,k),q[i].k=0;
  }
  if(!bit)
   break;
 }
 for(int i=1;i<=m;i++)
  printf("%lld\n",s[q[i].r]-s[q[i].l-1]-ans[i]);
 return 0;
}

来源：zr