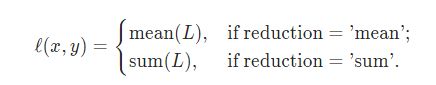含绝对值损失函数的优化分析

1、问题

在深度学习中，定义的损失函数含绝对值，如MAE，会存在一阶导数不连续，这时候在不连续的点处该如何进行反向传播?

2、L1损失函数的反向传播

绝对值函数求导
$$\frac{d}{dx}|u|=\frac{u}{|u|}\cdot \frac{du}{dx}$$

L1 损失函数
$$L1(p,y)＝\sum _{i=1}^n|p_i-y_i|$$

其中，$p$是预测值，$y$是目标值。

在pytorch中 L1 的实现：

torch.nn.functional.l1_loss(input, target, size_average=None, reduce=None, 
reduction='mean')

pytorch除了对损失函数求和，还支持求平均。

pytorch求L1函数的导数。

import torch
device = 'cpu'
pred = torch.tensor([-1,0,1], dtype=torch.float64, device=device, requires_grad=True)
y = torch.tensor([0,0,0], dtype=torch.float64, device=device)
loss = torch.nn.functional.l1_loss(pred, y, reduction='sum')
loss.backward()
print(pred.grad)

结果：

tensor([-1.,  0.,  1.], dtype=torch.float64)

换种方式来实现 l1 范数：

import torch
device = 'cpu'
pred = torch.tensor([-1,0,1], dtype=torch.float64, device=device, requires_grad=True)
y = torch.tensor([0,0,0], dtype=torch.float64, device=device)
def reduce(x, reduction="mean"):
    """Batch reduction of a tensor."""
    if reduction == "sum":
        x = x.sum()
    elif reduction == "mean":
        x = x.mean()
    elif reduction == "none":
        x = x
    else:
        raise ValueError("unkown reduction={}.".format(reduction))
    return x

def l1_loss(pred, target, reduction="mean"):
    """Computes the F1 loss with subgradient 0."""
    diff = pred - target
    loss = torch.abs(diff)
    loss = reduce(loss, reduction=reduction)
    return loss
loss = l1_loss(pred, y, reduction='sum')
loss.backward()
print(pred.grad)

结果：

tensor([-1.,  0.,  1.], dtype=torch.float64)

根据绝对值函数求导有：
$$\frac{d}{d{p}_i}sum|(p-y)|=\frac{p_i-y_i}{|p_i-y_i|}\cdot \frac{d(p_i-y_i)}{d{p}_i}=\frac{p_i-y_i}{|p_i-y_i|}$$

在 pred - y = 0 时， 导数是 0/0.

如果看 $|x|$ 函数在0 处的导数，应该是 -1 或 1，并不是一个确定的值， 一些平滑操作，会用 0 来代替。 其实也可以理解为损失都为0了，梯度就不需要更新了。

总而言之，含绝对值的损失函数的导数定义为定义成符号函数 sgn(x) ，用梯度下降法就能进行优化了。

3. 其他不处处可导损失函数

3.1 转为可导凸函数

把导数不连续的损失函数改成导数连续的函数。
比如，l1 loss 就有变种 smooth_l1_loss。

 0.5 * x^2                  if |x| <= 1         
  |x| - 0.5                  if |x| > 1    

def _smooth_l1_loss(input, target):
    # type: (Tensor, Tensor) -> Tensor
    t = torch.abs(input - target)
    return torch.where(t < 1, 0.5 * t ** 2, t - 0.5)

3.2 次梯度法

次梯度方法(subgradient method)是用来处理不可导的凸函数。
算法：
$$x^{(k+1)}=x^{(k)}-{\alpha }_k{g}^{(k)}$$

其中，$g^{(}k)$代表次梯度。
次梯度属于一个集合，比如 L1 在0处的次梯度为[-1,1].

3.3 近端梯度 (proximal gradient) 法

大致原理是说用目标函数往往形如 f(x) + g(x)，其中 f(x) 光滑而 g(x) 不光滑，可以用一个二次函数 q(x) 在局部近似 f(x)，而 q(x) + g(x) 的最优解是可以解析地求出的.

---

参考:

1. What is the derivative of an absolute value?;
2. L1 和 L2中的损失函数；
3. Github L1Loss / torch.abs gradient discrepancy;
4. pytorch L1Loss/smooth l1 loss;
5. Wiki huber_loss;
6. 【机器学习】次梯度（subgradient）方法;
7. zhihu L1的问题 Towser的回答；
8. Subgradients;