计量经济学之回归分析学习笔记(均值回归、分位数回归、岭回归、Lasso回归、ENet回归)——基于R(一)
【笔记前言】
最近在进行计量经济学的课程学习,本文对部分回归方法进行了整理,恳请大家对其中出现的错误进行指正,不胜感激。
此外,由于种种原因,在均值回归时,我们将涉及到模型建立后的后续检验,而在其他回归中,将着重于突出其参数估计的基本思路与过程,以及其各自之间的对比。同时,本系列学习笔记将使用R软件进行实践操作。
从参数估计的角度,各种方法都是目标函数的最优化问题,只是因为具体情况不同,使得各自约束条件不同,因此估计得到的参数也不同。映射到几何意义上,大致是在OLS的原始曲面下寻找新的最优解(根据约束域)。
这个笔记断断续续经历了一天的时间...后面有点潦草。
一、均值回归——简单线性回归
(一)一元线性回归
以iris数据集作为实验数据
>data=iris[,1:4]
>r1=lm(Sepal.Length~Sepal.Width,data)
>summary(r1)
Call:
lm(formula = Sepal.Length ~ Sepal.Width, data = data)
Residuals:
Min 1Q Median 3Q Max
-1.5561 -0.6333 -0.1120 0.5579 2.2226
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.5262 0.4789 13.63 <2e-16 ***
Sepal.Width -0.2234 0.1551 -1.44 0.152
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.8251 on 148 degrees of freedom
Multiple R-squared: 0.01382, Adjusted R-squared: 0.007159
F-statistic: 2.074 on 1 and 148 DF, p-value: 0.1519
>plot(data$Sepal.Width,data$Sepal.Length)
>abline(r1)
下附学习笔记。
(二)多元线性回归
>data=iris[,1:4]
>r1=lm(Sepal.Length~.,data)
>summary(r1)
Call:
lm(formula = Sepal.Length ~ ., data = data)
Residuals:
Min 1Q Median 3Q Max
-0.82816 -0.21989 0.01875 0.19709 0.84570
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.85600 0.25078 7.401 9.85e-12 ***
Sepal.Width 0.65084 0.06665 9.765 < 2e-16 ***
Petal.Length 0.70913 0.05672 12.502 < 2e-16 ***
Petal.Width -0.55648 0.12755 -4.363 2.41e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3145 on 146 degrees of freedom
Multiple R-squared: 0.8586, Adjusted R-squared: 0.8557
F-statistic: 295.5 on 3 and 146 DF, p-value: < 2.2e-16
二、分位数回归
(仅涉及参数估计部分,其中参数估计的具体方法都是运筹学中求解最优化问题的方法)
分位数回归不考虑同方差、正态分布的假设,具有异常点抗耐性、捕捉分布尾部特征等特点,更加稳健。
>library("quantreg")
>plot(data$Sepal.Length,data$Petal.Length)
>for(i in 1:length(taus))
+{abline(rq(Sepal.Length~Petal.Length,tau=taus[i],data))}>r2=rq(Sepal.Length~Petal.Length,tau=c(0.05,0.25,0.5,0.75,0.95),data)
>summary(r2)
Call: rq(formula = Sepal.Length ~ Petal.Length, tau = c(0.05, 0.25,
0.5, 0.75, 0.95), data = data)
tau: [1] 0.05
Coefficients:
coefficients lower bd upper bd
(Intercept) 3.92000 2.58928 3.98347
Petal.Length 0.34286 0.31021 0.55823
Call: rq(formula = Sepal.Length ~ Petal.Length, tau = c(0.05, 0.25,
0.5, 0.75, 0.95), data = data)
tau: [1] 0.25
Coefficients:
coefficients lower bd upper bd
(Intercept) 4.04000 3.90096 4.25598
Petal.Length 0.40000 0.33296 0.42847
Call: rq(formula = Sepal.Length ~ Petal.Length, tau = c(0.05, 0.25,
0.5, 0.75, 0.95), data = data)
tau: [1] 0.5
Coefficients:
coefficients lower bd upper bd
(Intercept) 4.35556 3.97856 4.52832
Petal.Length 0.38889 0.35981 0.43588
Call: rq(formula = Sepal.Length ~ Petal.Length, tau = c(0.05, 0.25,
0.5, 0.75, 0.95), data = data)
tau: [1] 0.75
Coefficients:
coefficients lower bd upper bd
(Intercept) 4.46122 4.38255 4.70718
Petal.Length 0.44898 0.40547 0.46551
Call: rq(formula = Sepal.Length ~ Petal.Length, tau = c(0.05, 0.25,
0.5, 0.75, 0.95), data = data)
tau: [1] 0.95
Coefficients:
coefficients lower bd upper bd
(Intercept) 4.97037 4.84742 5.10100
Petal.Length 0.40741 0.39096 0.46906 
下附学习笔记。
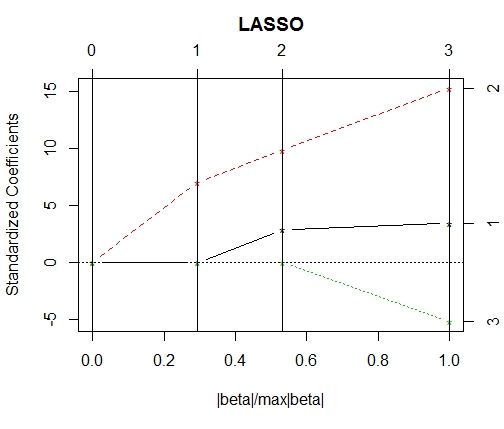
三、岭回归、Lasso回归、ENet回归——带惩罚函数的OLS估计
很清楚可以看出,都是目标函数有变化
library(MASS)
plot(lm.ridge(Sepal.Length~.,iris,lambda=seq(0,10,0.5)))
regression=lm.ridge(Sepal.Length~.,data)
plot(lm.ridge(Sepal.Length~.,data,lambda=seq(0,10,0.5)))
select(lm.ridge(Sepal.Length~.,data,lambda=seq(0,10,0.5)))具体的参数选择可以在R软件help到
library(lars)
data2=as.matrix(data)
regression2=lars(data2[,2:4],data2[,1])
plot(regression2)