四连测全题解

第一次：

一 . 猴子

时间限制: 1 Sec  内存限制: 128 MB

题目描述、输入、输出

       ----------------

方法

B此题的基本方法是DP，很好理解，状态转移方程是  。

因为数据量很大，所以要用到单调队列来优化。

普通的单调队列是单纯地上升或下降..但这次是有区别的。

黄*：

我们看状态转移方程，其中的j是有一个范围的，就是 i - k + 1 <= j <= i - 1。又是求最小值，我们便可以想到些什么东西

维护队列中元素递增，并且判断队首元素是否在区间内。这样就得到了最小的dp[i]了。但怎么确定优先级呢。对于不同的高度还有加1和不加1的这一种情况呢。难道要将全部放进单调队列中吗？

答案是否定的。我们姑且抛掉后面的比较。先讨论一下最小的dp[j]

（一）如果dp[j]最小且唯一，就假设它加上1吧。还是最小的，肯定可以选啊。这种情况很好讨论。

（二）如果有多个最小值，我们便需判断一下了，我们想想，说不定这些j所在的高度是有些需要加1，但有些是不需要加1的，那么，不需要加1的那一些高度肯定优于其他的那些高度。但我们又不确定是否不用加1，但我们不考虑这么多，在这些最小值找到一个最高的。最后判断就行了，如果它不用+1，那是最好的，如果它要+1，其他的也一样的。于是我们便讨论完了所有情况，可以用单调队列来做了

（老师说发真代码考验人品，我从此就不发图片了）

#include
#include
#include
#define push()
using namespace std;
void read(int &x) {
    int f=1;x=0;char s=getchar();
    while(s<'0'||s>'9') {if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
    x*=f;
}
struct no{
    int dp,id;
    no(){}
    no(int D,int I){dp = D;id = I;}
}q[1000005];
int n,m,i,j,s,o,k,f = 1,l = 1;
int t[27],a[1000005];
bool operator > (no x,no y) {
    return x.dp > y.dp || ( x.dp == y.dp && a[x.id] < a[y.id] );
}
int main() {
    read(n);
    for(i = 1;i <= n;i ++) {
        read(a[i]);
    }
    read(m);
    for(i = 1;i <= m;i ++) {
        read(t[i]);
        f = 1,l = 1;
        q[f] = no(0,1);
        for(j = 2;j <= n;j ++) {
            if(a[q[f].id] > a[j]) {
                //push();
                while(l > f && q[l] > no(q[f].dp,j)) {
                    l --;
                }
                q[++ l] = no(q[f].dp,j);
                if(j == n) k = q[f].dp;
            }
            else {
                //push(q[++ l],no(q[f].dp + 1,j));
                while(l > f && q[l] > no(q[f].dp + 1,j)) {
                    l --;
                }
                q[++ l] = no(q[f].dp + 1,j);
                if(j == n) k = q[f].dp + 1;
            }
            while(q[f].id <= j - t[i]) f ++;
        }
        printf("%d\n",k);
    }
    return 0;
}
 

二 . 电话线路

时间限制: 1 Sec  内存限制: 128 MB

题目描述、输入、输出

     ----------------------

方法

纯DP方法就行，有点简单，但一开始我没做出来。

#include
#include
#include
using namespace std;
void read(int &x) {
    int f=1;x=0;char s=getchar();
    while(s<'0'||s>'9') {if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
    x*=f;
}
int n,m,i,j,s,o,k = 0x7f7f7f7f,c,maxh,min1,min2;
int dp[100005][105],a[100005];
int main() {
    read(n);read(c);
    for(i = 1;i <= n;i ++) {
        read(a[i]);
        maxh = max(maxh,a[i]);
    }
    for(j = 1;j <= maxh;j ++) {
        if(j < a[1]) dp[1][j] = 0x7f7f7f7f;
        else dp[1][j] = (j - a[1]) * (j - a[1]);
    }
    for(i = 2;i <= n;i ++) {
        min1 = min2 = 0x7f7f7f7f;
        for(j = 1;j <= maxh;j ++) {
            min1 = min(min1,dp[i - 1][j] - j * c);
            if(j >= a[i]) {
                dp[i][j] = min1 + (j - a[i]) * (j - a[i]) + j * c;
            }
            else dp[i][j] = 0x7f7f7f7f;
        }
        for(j = maxh;j >= a[i];j --) {
            dp[i][j] = min(dp[i][j],min2 + (j - a[i]) * (j - a[i]) - j * c);
            min2 = min(min2,dp[i - 1][j] + j * c);
        }
    }
    for(j = a[n];j <= maxh;j ++) {
        k = min(k,dp[n][j]);
    }
    printf("%d",k);
    return 0;
}
 

 

第二次：

            [第二场考试]

第三次：

一 . 圆形谷仓

          [我的题解]

二 . 篱笆

时间限制: 1 Sec  内存限制: 128 MB

题目描述、输入、输出

       ------------

方法

把它转化得类似迷宫，然后就是最小生成树了。

虽然很像最小生成树，但这个图有点过于单调了，且每一整排/列的篱笆长度都一样，于是就可以用贪心法了。

因为它的单调性，所以就把每一种篱笆长度排个序，依次进行整行整列地打通，若有没必要的，即将要形成环的，就不拆了。

还是因为它的单调性，所以判断环是很简单的，甚至不需要判断，就用变量记录就行。

自己从代码中体会：

#include 
#include 
#include 
#include 
#define ll long long 
using namespace std; 
void read(int &x) { 
    int f = 1;x = 0;char s = getchar(); 
    while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();} 
    while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();} 
    x *= f; 
} 
int n,m,i,j,k,o,xx,yy,he = 0,su = 0,x = 1,y = 1; 
ll ans; 
int h1[2005],s1[2005]; 
int h[2005],s[2005]; 
int main() { 
    read(xx);read(yy);read(n);read(m); 
    for(i = 1;i <= n;i ++) { 
        read(h1[i]); 
    }h1[n + 1] = xx; 
    for(i = 1;i <= m;i ++) { 
        read(s1[i]); 
    }s1[m + 1] = yy; 
    sort(h1 + 1,h1 + 1 + n); 
    sort(s1 + 1,s1 + 1 + m); 
    for(i = n + 1;i > 0;i --) { 
        h[i] = h1[i] - h1[i - 1]; 
    } 
    for(i = m + 1;i > 0;i --) { 
        s[i] = s1[i] - s1[i - 1]; 
    } 
    sort(h + 1,h + 2 + n); 
    sort(s + 1,s + 2 + m); 
    ans += (ll)h[x++] * ((ll)m - he); 
    ans += (ll)s[y++] * ((ll)n - su); 
    while(x <= n + 1 && y <= m + 1) { 
        if(h[x] <= s[y]) { 
            ans += (ll)h[x++] * ((ll)m - he); 
            su ++; 
        } 
        else { 
            ans += (ll)s[y++] * ((ll)n - su); 
            he ++; 
        } 
    } 
    printf("%lld",ans); 
    return 0; 
} 
  

第四次：

一 . 谷仓

时间限制: 1 Sec  内存限制: 128 MB

题目描述

有一个圆形的谷仓，共有n个房间，按顺时针编号从1到n。现在有许多头奶牛，他们都有自己最喜欢的一个房间。傍晚回家时，奶牛们去找自己最喜欢的房间。如果发现被占了，他们就会按照顺时针方向找第一个空闲的房间住进去。现在请你输出最小的空闲的房间号。注意，这个答案和奶牛们回家的顺序是无关的。

2<=n<=3000000,1<=k<=10000,A,B的值在区间[0,10^9]。

输入

输入格式：

第一行两个整数n，k。

接下来有k行。每行4个整数，x,y,a,b.表示有x头奶牛喜欢f[1],f[2]……，f[y]。其中f[i]=(a*i+b)%n+1.

输出

输出格式：

输出最小的空闲房间号。

方法

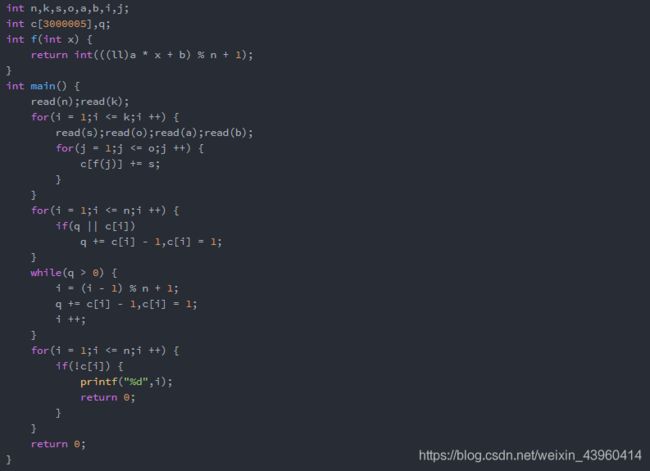
此题跟圆形谷仓区别不大，只是用正序循环，最多两次，内容简单，不会超时。

二 . 拥挤的奶牛

时间限制: 1 Sec  内存限制: 128 MB

题目描述

FJ的n头奶牛（1<=n<=50000）在被放养在一维的牧场。第i头奶牛站在位置x(i)，并且x(i)处有一个高度值h(i)

（1<=x(i),h(i)<=1000000000）。

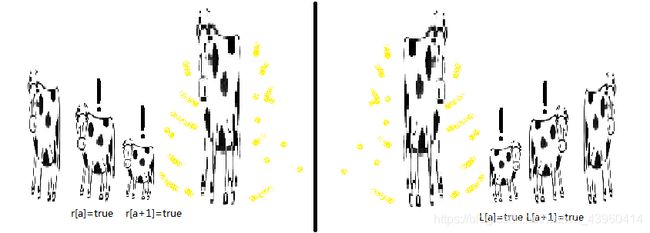
一头奶牛感觉到拥挤当且仅当它的左右两端都有一头奶牛所在的高度至少是它的2倍，且和它的距离最多为D。尽管感到拥挤的奶牛会产生更少的牛奶，FJ还是想知道一共有多上感到拥挤的奶牛。请你帮助他。

输入

第一行：两个整数n和D。

第二行到第n+1行：每一行有两个数表示x(i)和h(i)。

输出

 一个数k表示感到拥挤的奶牛的数量。

方法

这道题确实烧脑，因为它没办法用单调队列去存。 假设 i 大于队末元素 j ，则在普通的下降单调队列中， j 就因该被计算并且出队，但是若 i 并不大于等于 2 * j ，就不能计算 j 。若此时把 i 直接入队，就缺乏单调性，不方便计算了。

既然此题数据过大，需要优化，却又不能用单调队列/栈的话，能不能只利用它 O(2n) 的优点，采用更灵活的结构呢？

       我的想法是，先按照位置排序，然后用一个优先队列，令 (node)a < b 为 a.h < b.h，用小根堆优化。跟单调队列差不多。每次有元素 x 入堆，就先把堆顶(最矮的那些)身高不超过  的奶牛计算了，如果有与 x 的距离超过 D 的，就直接出堆，然后再把 x 入堆。计算两遍，一次计算右边有无拥挤，一次计算左边。

这样一来，每个元素仍然只有 入堆，出堆 两种计算，时间复杂度也还是 n 的常数倍！

#include
#include
#include
#include
#include
using namespace std;
void read(int &x) {
    int f = 1;x = 0;char s = getchar();
    while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
    while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
    x *= f;
}
struct no{
    int id,x,h;
}a[50005];
bool operator < (no a,no b) {
    return a.h < b.h;
}
bool operator > (no a,no b) {
    return b < a;
}
int n,m,s,o,i,j,k;
bool l[50005],r[50005];
priority_queue,greater > b;
bool cmp(no a,no b) {
    return a.x < b.x;
}
int main() {
    read(n);read(m);
    for(i = 1;i <= n;i ++) {
        read(a[i].x);read(a[i].h);
        a[i].id = i;
    }
    sort(a + 1,a + 1 + n,cmp);
    b.push(a[1]);
    for(i = 2;i <= n;i ++) {
        while(!b.empty() && a[i].h >= b.top().h * 2) {
            if(a[i].x - b.top().x <= m) {
                r[b.top().id] = 1;
            }
            b.pop();
        }
        b.push(a[i]);
    }
    while(!b.empty()) b.pop();
    b.push(a[n]);
    for(i = n - 1;i > 0;i --) {
        while(!b.empty() && a[i].h >= b.top().h * 2) {
            if(b.top().x - a[i].x <= m) {
                l[b.top().id] = 1;
            }
            b.pop();
        }
        b.push(a[i]);
    }
    for(i = 1;i <= n;i ++) {
        if(l[i] && r[i]) k ++;
    }
    printf("%d",k);
    return 0;
}

我现在看了别人的题解后才发现原来还可以用单调~的方法，只不过要变一下思维：[用单调~的方法]。

三 . 弹簧高跷

时间限制: 1 Sec  内存限制: 128 MB

题目描述、输入、输出

          ------------

方法

这道题用DP是可以解决的。因为每一次跳跃都与前一次跳跃有关，也就是说，每次要枚举前两次的跳跃落点，然后才能计算出某点到一个落点的最优解。这样一来，就可以定义一个 f [ ] [ ] ，f[ i ][ j ] 表示 以 “ 从 i 点跳到 j 点 ” 结束 的 一整次跳跃过程 中，得到的最高分 (注意: 可能是 i < j，也可能是 i > j，当然也有 i = j 的情况)。状态转移方程：

   (分数)

先处理 f[ i ][ i ] 的情况，然后正逆序都进行一次三重循环。

#include
#include
#include
#include
#include
using namespace std;
void read(int &x) {
    int f = 1;x = 0;char s = getchar();
    while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
    while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
    x *= f;
}
struct no{
    int x,h;
}a[1005];
bool operator < (no a,no b) {
    return a.x < b.x;
}
bool operator > (no a,no b) {
    return b < a;
}
int n,m,s,o,i,j,k,ans = 0;
int dp[1005][1005];
int main() {
    read(n);
    for(i = 1;i <= n;i ++) {
        read(a[i].x);read(a[i].h);
        ans = max(ans,a[i].h);
    }
    sort(a + 1,a + 1 + n);
    for(i = 1;i <= n;i ++) {
        dp[i][i] = a[i].h;
        for(j = 1;j < i;j ++) {
            dp[j][i] = dp[j][j];
            for(k = j - 1;k > 0 && a[j].x - a[k].x <= a[i].x - a[j].x;k --) {
                dp[j][i] = max(dp[j][i],dp[k][j]);
            }
            dp[j][i] += a[i].h;
            ans = max(ans,dp[j][i]);
        }
    }
    for(i = n;i > 0;i --) {
        for(j = n;j > i;j --) {
            dp[j][i] = dp[j][j];
            for(k = j + 1;k <= n && a[k].x - a[j].x <= a[j].x - a[i].x;k ++) {
                dp[j][i] = max(dp[j][i],dp[k][j]);
            }
            dp[j][i] += a[i].h;
            ans = max(ans,dp[j][i]);
        }
    }
    printf("%d",ans);
    return 0;
}
 

四 . 滑雪场的高度差

时间限制: 1 Sec  内存限制: 128 MB

题目描述

滑雪场可以看成M x N的网格状山地(1 <= M,N <= 500),每个网格是一个近似的平面，具有水平高度值在0 .. 1,000,000,000米的范围内。

某些网格被指定为关键网格。当两个相邻网格之间的高度差的绝对值不超过某个参数D时，就可以相互到达。相邻关系是指某个格子的东、西、南、北的格子。

显然，当D不断减小时，原本可以相互到达的相邻格子就不能到达了。

滑雪赛的组委会想知道，为了保证各个关键网格之间彼此连通，最小的D是多少？

输入

 第1行：2个整数M和N

接下来M行，每行N个整数，表示各网格的高度

接下来M行，每行N个0或者1，1表示关键网格

输出

 第1行：1个整数，表示最小的D

方法

因为这题和二分求解有一个共同点。即  若 D = x 时，关键网格之间彼此连通，则 D = (x + 1) 时，关键网格之间肯定更彼此连通，所以就跟 “ 在单调序列中寻找值 ” 有相同点了。故此题要用二分 + 搜索 求解。

（XYF：）至于搜索，优选bfs（节省时间）。在合法情况下搜索一次（起点下文解释），存哪些网格经历过，最后再判断是否经过了所有关键网格。起点最先想到的肯定是从每一个关键网格出发，看看从它开始搜索，在合法情况下是否能经过所有关键网格（输入时可以用结构体，存下每一个关键网格的坐标，关键网格的数量）。但试想，从任意一个关键网格出发，如果它能经过所有关键网格，这个mid就是可以采用的呢？因为假如从某一关键网格（x,y）出发，它通过某一路径经过一个关键网格（m,n），那么从（m,n）出发也一定能通过这个路径，以现在的 mid 经过（x,y）。所以假如（x,y）能经过所有的关键网格，那么（m,n）也一定能经过所有的关键网格（它先沿某一路径到达（x,y））。所以只用从任意一个关键网格开始搜索，再判断。如果它经过了所有关键网格，bfs() 返回true，不然返回false。

其中有一些小坑，曾经把我害的惨，

1，要用 bfs 的话，vis[][] 的计算，清空，判断很重要。

2，二分防爆。

->    3，若要用 “ while(l < r) ” 的人注意，退出循环后，mid 还没更新成 (l + r) / 2，除非在循环节末尾更新 mid ，不然不能直接输出 mid 。

4，判断绝对值 abs() 函数最好不要用宏定义，不然要错，除非使用时这样写：abs( ( ...... ) ) 。

以下代码：(考察良心的时候到了)

#include
#include
#include
#include
#include
#define abs(x) (x < 0 ? -x : x)
using namespace std;
void read(int &x) {
    int f = 1;x = 0;char s = getchar();
    while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
    while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
    x *= f;
}
struct no{
    int x,y;
    no(){}
    no(int X,int Y){
        x = X;y = Y;
    }
};
int n,m,s,o,i,j,k,ans = 0,nm,fx,fy,ji = 0;
int a[505][505],d[4][2] = {{1,0},{0,1},{-1,0},{0,-1}};
bool f[505][505],v[505][505];
bool bfs(int xx) {
    memset(f,0,sizeof(f));
    ji = 0;
    queue b;
    b.push(no(fx,fy));
    f[fx][fy] = 1;
    while(!b.empty()) {
        no t = b.front();
        b.pop();
        if(v[t.x][t.y]) {
            ji ++;
        }
        if(ji == nm) {
            return 1;
        }
        for(int i = 0;i < 4;i ++) {
            no t1 = t;
            t1.x += d[i][0];
            t1.y += d[i][1];
            if(!f[t1.x][t1.y] && t1.x > 0 && t1.x <= n && t1.y > 0 && t1.y <= m && abs((a[t1.x][t1.y] - a[t.x][t.y])) <= xx) {
                f[t1.x][t1.y] = 1;
                b.push(t1);
            }
        }
    }
    return 0;
}
int js(int l,int r) {
    int mid = (l + r) / 2;
    while(l < r) {
        bool ff = bfs(mid);
        if(ff) r = mid;
        else l = mid + 1;
        mid = (l + r) / 2;
    }
    return mid;
}
int main() {
    read(n);read(m);
    for(i = 1;i <= n;i ++) {
        for(j = 1;j <= m;j ++) {
            read(a[i][j]);
            o = max(o,a[i][j]);
        }
    }
    for(i = 1;i <= n;i ++) {
        for(j = 1;j <= m;j ++) {
            read(k);
            if(k == 1) v[i][j] = 1,fx = i,fy = j,nm ++;
        }
    }
    printf("%d",js(0,o));
    return 0;
}
 

->【我的总结】<-