基于python3计算机视觉编程(五)照相机模型及张正友相机标定算法

一. 针孔照相机模型原理

针孔相机模型就是把相机简化成小孔成像， 比较基础简单的投影变换有正交变换和透视变换。正交变换就是物体上的点全都平行地投射到投影面，没有远近的区别，即没有透视效果。透视变换正好相反，被投影物体处于一个四棱台区域中，物体被投影到离相机较近的平面上。相机被抽象为一个点，而投影点是物体上的点和相机的连线与投影平面的交点。


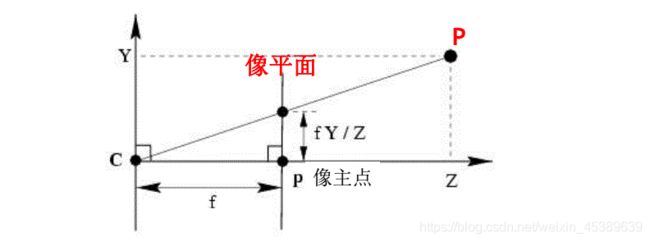
其中空间点$C$是投影中心，它到平面的距离称为焦距。并且空间点$P$在平面上的投影$p$是以点$C$为端点并经过点$p$射线与平面的交点。这个平面叫做相机的像平面。点$C$为光心。总结如下：

• $C$ 点即相机的中心点，也是相机坐标系的中心点；
• $Z$ 即相机的主轴；
• $P$ 点即相机的像平面，也就是图片坐标系所在的二维平面；
• $p$ 即主点，主轴与像平面相交的点；
• $C$ 点到 $p$ 点的距离，即相机的焦距；

1.1 世界转换到相机

如上图所示），从世界坐标系转换到相机坐标系是三维空间到三维空间的变换，一般来说需要一个平移操作和一个旋转操作就可以完成这个转换，用公式表示如下（可以理解为世界坐标系原点先平移到相机坐标系的位置然后在做一次坐标系旋转，使坐标轴对齐。）：

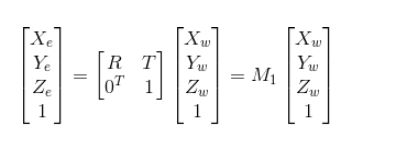
其中$R$称为旋转矩阵，$T$为三维平移向量，经过变换后两个变量整合进了$M$中:

当中的平移参数$tx$,$ty$,$tz$以及旋转参数$rx$,$ry$,$rz$这六个参数为照相机的外参数。

1.2 相机转换到像平面

相机坐标系中的一个点 $X$（现实三维世界中的点），在像平面坐标系对应的点是 $x$，要求从相机坐标系转为像平面坐标系的转换，也就是从 $X$ 点的$(X,Y,Z)$通过一定的转换变为 $x$ 点的$(x,y)$。$(X,Y,Z)$是在相机坐标系，而$(x,y)$是在像平面坐标系。根据观察上图，可以看出两个三角形为相似三角形。于是可以得出以下公式：

$x=fX/Z$
$y=fY/Z$
$(X,Y,Z)\mapsto (fX/Z,fY/Z)$

可以转换成如下的矩阵计算:

二. 相机参数

相机的内参数分别为：

• 焦距
• 像主点的坐标
• 畸变参数

设 $P=(X,Y,Z)$ 为场景中的一点，进行下面几个步骤：

1. 将 $P$ 从世界坐标系通过刚体变换变换到相机坐标系，这个变换过程使用的是相机间的相对位姿，也就是相机的外参数。
2. 从相机坐标系，通过透视投影变换到相机的成像平面上的像点$p=(x,y)$。
3. 将像点$p$从成像坐标系，通过缩放和平移变换到像素坐标系上点$p=(\mu ,\nu )$。

我们就可以将场景中的三维点转换成图像中的二维点了。上述的变换步骤转换成具体的数学形式：

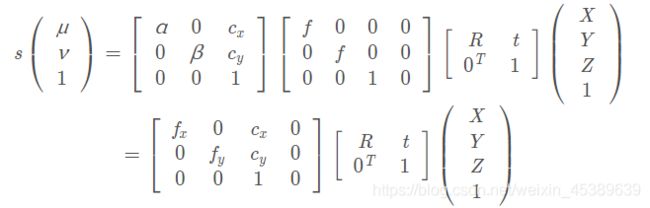
将矩阵K称为相机的内参数：

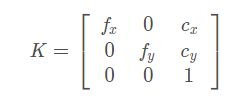
畸变参数
在几何光学和阴极射线管(CRT)显示中，畸变（distortion） 是对直线投影（rectilinear projection）的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。那畸变简单来说就是一条直线投影到图片上不能保持为一条直线了，这是一种光学畸变（optical aberration）。可能由于摄像机镜头的原因，这里不讨论，有兴趣的可以查阅光学畸变的相关的资料。
畸变一般可以分为两大类，包括径向畸变和切向畸变。主要的一般径向畸变有时也会有轻微的切向畸变。

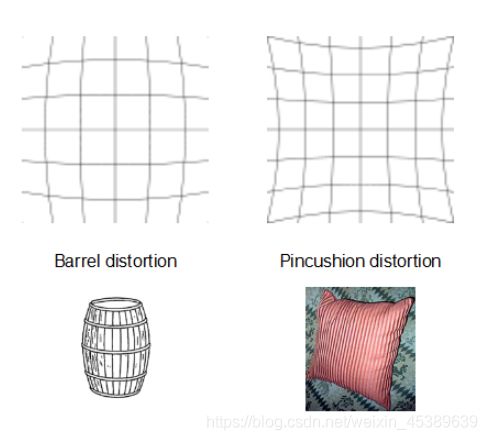
径向畸变
径向畸变的效应有三种，一种是桶形畸变（barrel distortion），另一种是枕形畸变（pincushion distortion）从图片中可以很容易看出区别，具体见下图：

三. 相机标定实现

3.1 相机标定原理

标定照相机是指计算出该照相机的内参数。标定照相机的标准方法是，拍摄多幅平面棋盘模式的图像，然后进行处理计算。由于光线在远离透镜中心的地方比靠近中心的地方更加弯曲或是透镜质量原因，图像会产生径向畸变。

计算内参与外参的初值

通过上文可以很容易推导出，一个三维空间的点转换到像平面，他们之间的单应性关系可以表示为：

其中s为尺度因子，K为内参矩阵，$R,t$分别为旋转矩阵和平移向量，令K:

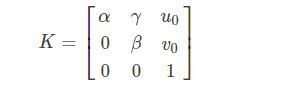
$(Uo,Vo)$为像主点坐标， $\alpha \beta$为焦距与像素横纵比的融合。 $\gamma$为畸变系数。s对于齐次坐标来说，不会改变齐次坐标值。张氏标定法中，将世界坐标系狗仔在棋盘格平面上，令棋盘格平面为 $Z=0$的平面。则可得：

我们把$K[r1,r2,t]$叫做单应性矩阵$H$，即：

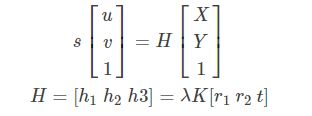
$H$是描述Homography矩阵，可以通过最小二乘，从角点世界坐标到图像坐标的关系求解。Homography有8个自由度，即8个未知量，所以最少需要8个方程，而每个对应点能提供两个方程，所以至少需要4个对应点，才能算出$H$矩阵。通过上式的矩阵运算，根据$r1$，$r2$正交，以及归一化的约束可以得到下面的式子：

即每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。为了方便计算，定义如下：

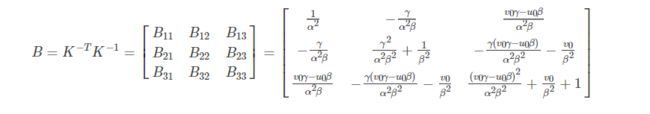
可以观察出该阵是个对称阵，于是$B$可以表示成6D向量$b$:

可以推导出：

利用约束条件：

通过上式，我们至少需要三幅包含棋盘格的图像，可以计算得到B，然后通过cholesky分解，得到相机的内参数矩阵K：

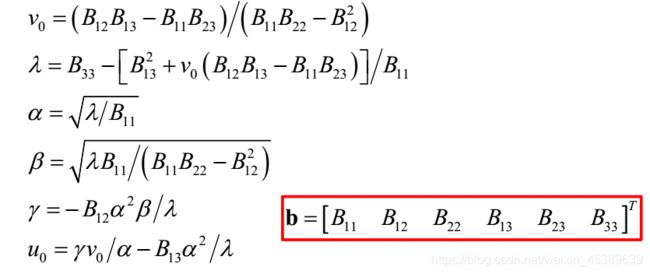
最大似然估计

上述的推导结果是基于理想情况下的解，但由于可能存在高斯噪声，所以使用最大似然估计进行优化。

其思想就是以迭代的方法求出整个式子的最小值。而这类非线性优化类问题可以利用Levenberg-Marquardt算法求解。

3.2 实验

标记步骤：

1. 打印一张棋盘格，把它贴在一个平面上，作为标定物。
2. 通过调整标定物或摄像机的方向，为标定物拍摄一些不同方向的照片（一般10~20张）。
3. 从照片中提取棋盘格角点（Harris特征）。
4. 估算理想无畸变的情况下，五个内参和六个外参。
5. 应用最小二乘法估算实际存在径向畸变下的畸变系数。
6. 极大似然法，优化估计，提升估计精度。

数据集准备：
原始图像为5X5的黑白棋盘格，每个格子3cm。代码使用的是GitHub上的开源代码，这里附上链接(https://github.com/SPengLiang/Camera-Calibration-of-Zhang-s-method)

随后以不同角度拍摄，并且将图片做了灰度处理，因图片太大会影响运行效率，所以进行了统一的压缩。

出现的错误：

在运行过程中，我们所要采用计算的是棋盘格的内角点，而不包括外角点，若是出现这种错误可以检查看看自己函数中所代入的角点是否有误。

解决方法：

修改上图红框标注中的值，这需要根据我们自身设置的棋盘尺寸来修改，例如我用的棋盘格子是5X5，实际上用的参数是4X4，及只考虑内角点，不考虑外角点。

主函数：

import cv2 as cv
import numpy as np
import os
from step.homography import get_homography
from step.intrinsics import get_intrinsics_param
from step.extrinsics import get_extrinsics_param
from step.distortion import get_distortion
from step.refine_all import refinall_all_param


def calibrate():
    # 求单应矩阵
    H = get_homography(pic_points, real_points_x_y)

    # 求内参
    intrinsics_param = get_intrinsics_param(H)

    # 求对应每幅图外参
    extrinsics_param = get_extrinsics_param(H, intrinsics_param)

    # 畸变矫正
    k = get_distortion(intrinsics_param, extrinsics_param, pic_points, real_points_x_y)

    # 微调所有参数
    [new_intrinsics_param, new_k, new_extrinsics_param] = refinall_all_param(intrinsics_param,
                                                                             k, extrinsics_param, real_points,
                                                                             pic_points)

    print("intrinsics_parm:\t", new_intrinsics_param)
    print("distortionk:\t", new_k)
    print("extrinsics_parm:\t", new_extrinsics_param)


if __name__ == "__main__":
    file_dir = 'E:/photogray/'
    # 标定所用图像
    pic_name = os.listdir(file_dir)

    # 由于棋盘为二维平面，设定世界坐标系在棋盘上，一个单位代表一个棋盘宽度，产生世界坐标系三维坐标
    cross_corners = [4, 4]  # 棋盘方块交界点排列
    real_coor = np.zeros((cross_corners[0] * cross_corners[1], 3), np.float32)
    real_coor[:, :2] = np.mgrid[0:4, 0:4].T.reshape(-1, 2)

    real_points = []
    real_points_x_y = []
    pic_points = []

    for pic in pic_name:
        pic_path = os.path.join(file_dir, pic)
        pic_data = cv.imread(pic_path)

        # 寻找到棋盘角点
        succ, pic_coor = cv.findChessboardCorners(pic_data, (cross_corners[0], cross_corners[1]), None)

        if succ:
            # 添加每幅图的对应3D-2D坐标
            pic_coor = pic_coor.reshape(-1, 2)
            pic_points.append(pic_coor)

            real_points.append(real_coor)
            real_points_x_y.append(real_coor[:, :2])
    calibrate()

结果截图：
手机型号：华为Nova2Plus

intrinsics_parm为内参，一个相机只有一个内参，distortionk为畸变系数K，extrinsics_parm为外参数，接下来的数据则为每一张图片的参数，因为拍摄角度的不同所以每一张的外参也不相同，有12张图片就有12个外参。