抛物型差分（二维—ADI格式）

抛物型差分（二维—ADI格式）

 example : 模拟四方边界 ， 上：100°、下：0°、左：75°、右：50°

//getStart.m // simulate 
function getStart()
clc
X_INTERVAL = [0 20];
Y_INTERVAL = [0 30];
T = [ 0 10];
deltax = 0.5;
deltay = 0.3;
tao = 1 /3 * min(deltax ,deltay)^2;
m = (X_INTERVAL(2) - X_INTERVAL(1)) /deltax - 1; 
n = (Y_INTERVAL(2) - Y_INTERVAL(1)) /deltay - 1;
m = int32(m);
n = int32(n); 
A = ComputeA( m,n, tao/deltax^2 ,tao/deltay^2, (T(2) - T(1))/tao);
ASize = size(A);
m = ASize(1);
n = ASize(2);
x = linspace(X_INTERVAL(1) , X_INTERVAL(2),m)';
y = linspace(Y_INTERVAL(1) ,Y_INTERVAL(2) ,n);
surf(y,x,A)
 
//oneIter.m // 一步分解
function y = oneIter( A ,r_lf , r_rt)
 
A_size = size(A);
m = A_size(2) - 2;
n = A_size(1) - 2;
% create init ImpMatrix M and b
M = diag( ones(1,m)) * ( 1 + r_lf) + diag( ones(1,m - 1),1)* ( - r_lf /2) +...
        diag( ones(1,m - 1), -1) * ( -r_lf /2);
B = A;
for j = 2 : n + 1
    b = zeros( m ,1);
    rowA = A(j,:);
    b(1) = b(1) + rowA(1) * r_lf/2;
    b(m) = b(m) + rowA(m) * r_lf/2;
    for i = 2 : m + 1
        colA = A(j-1:j+1,i);
        b(i - 1) = b(i - 1) + r_rt /2 * colA(1) + (1 - r_rt) * colA(2) +...
            r_rt /2 * colA(3);
    end
    B(j, 2: m+1) = M\b;
end
    
y = B;
 
// ComputeA.m
function y = ComputeA(m,n,rx,ry ,iter)
A = createMatrix(m,n);
fprintf(' total iter = %d',iter);
//pause(100);
for i = 1:iter
    fprintf(' Iter num = %d\n' ,i);
    A = oneIter(A , rx, ry);
    B = oneIter(A',ry, rx);
    A = B';
end
y = A;
//createMatrix.m
function y = createMatrix(m ,n)
A = zeros(n + 2, m + 2);
Up = ones( m + 2 ,1) * 100;
Down = ones( m + 2,1) * 0;
Lf = ones( 1, n + 2) * 75;
Rt = ones( 1, n + 2) * 50;
A(1 ,:) = Up;
A( n + 2,:) = Down;
A(: , 1) = Lf;
A(:, m + 2) = Rt;
y = A;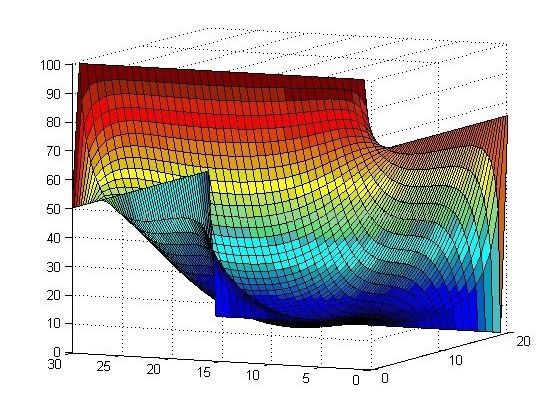

注：1.画图时，左右边界倒了，不想去改了，作图的问题
   2.ADI表现为分别在x ,y 方向上做一次单独的隐式差分，故在ComputeA.m中只需旋转一次矩阵再做一次迭代即可完成一次
     时间t的迭代