【算法系列（一）】：分治

目录

一、基本思想

二、解题思路

三、分治算法一般框架

四、算法应用 

169. 多数元素

53. 最大子序和

50. Pow(x, n) 

---

在计算机科学中，分治法是构建基于多项分支递归的一种很重要的算法范式。字面上的解释是「分而治之」，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

这个技巧是很多高效算法的基础，如排序算法（快速排序、归并排序）、傅立叶变换（快速傅立叶变换）。

另一方面，理解及设计分治法算法的能力需要一定时间去掌握。正如以归纳法去证明一个理论，为了使递归能够推行，很多时候需要用一个较为概括或复杂的问题去取代原有问题。而且并没有一个系统性的方法去适当地概括问题。

分治法这个名称有时亦会用于将问题简化为只有一个细问题的算法，例如用于在已排序的列中查找其中一项的折半搜索算法。这些算法比一般的分治算法更能有效地运行。其中，假如算法使用尾部递归的话，便能转换成简单的循环。但在这广义之下，所有使用递归或循环的算法均被视作“分治算法”。因此，有些作者考虑“分治法”这个名称应只用于每个有最少两个子问题的算法。而只有一个子问题的曾被建议使用减治法这个名称。

分治算法通常以数学归纳法来验证。而它的计算成本则多数以解递归关系式来判定。

一、基本思想

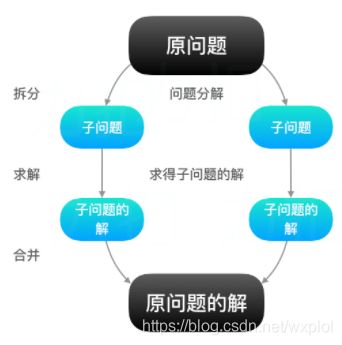
分治算法的主要思想是将原问题递归地分成若干个子问题，直到子问题满足边界条件，停止递归。将子问题逐个击破(一般是同种方法)，将已经解决的子问题合并，最后，算法会层层合并得到原问题的答案。

二、解题思路

• 分：递归地将问题分解为各个的子问题(性质相同的、相互独立的子问题)；
• 治：将这些规模更小的子问题逐个击破；
• 合：将已解决的子问题逐层合并，最终得出原问题的解；

分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

分治法适用的情况：

• 原问题的计算复杂度随着问题的规模的增加而增加。
• 原问题能够被分解成更小的子问题。
• 子问题的结构和性质与原问题一样，并且相互独立，子问题之间不包含公共的子子问题。
• 原问题分解出的子问题的解可以合并为该问题的解。

三、分治算法一般框架

伪代码：

def divide_conquer(problem, paraml, param2,...):
    # 不断切分的终止条件
    if problem is None:
        print_result
        return
    # 准备数据
    data=prepare_data(problem)
    # 将大问题拆分为小问题
    subproblems=split_problem(problem, data)
    # 处理小问题，得到子结果
    subresult1=self.divide_conquer(subproblems[0],p1,..…)
    subresult2=self.divide_conquer(subproblems[1],p1,...)
    subresult3=self.divide_conquer(subproblems[2],p1,.…)
    # 对子结果进行合并 得到最终结果
    result=process_result(subresult1, subresult2, subresult3,...)

四、算法应用 

169. 多数元素

• 题目描述

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 [n/2] 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。

示例 1:

输入: [3,2,3]
输出: 3

示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

• 解题思路
  • 确定切分的终止条件：直到所有的子问题都是长度为 1 的数组，停止切分。
  • 准备数据，将大问题切分为小问题：递归地将原数组二分为左区间与右区间，直到最终的数组只剩下一个元素，将其返回
  • 处理子问题得到子结果，并合并：
  1. 长度为 1 的子数组中唯一的数显然是众数，直接返回即可。
  2. 如果它们的众数相同，那么显然这一段区间的众数是它们相同的值。
  3. 如果他们的众数不同，比较两个众数在整个区间内出现的次数来决定该区间的众数
• c++代码实现

int countRange(vector &nums,int value,int left,int right){
    int count=0;
    for(int i=left;i<=right;++i){
        if(nums[i]==value) count++;
    }
    return count;
}

int majorityElementRec(vector &nums,int left,int right){
    if(left==right){
        return nums[left];
    }

    int mid=left+(right-left)/2;
    int l=majorityElementRec(nums,left,mid);
    int r=majorityElementRec(nums,mid+1,right);
    if(l==r) return l;

    int l_count=countRange(nums, l, left, right);
    int r_count=countRange(nums,r,left,right);

    return l_count>r_count?left:right;

}


int majorityElement(vector& nums) {
    return majorityElementRec(nums,0,nums.size()-1);
}

53. 最大子序和

• 题目描述

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大为6。

• 解题思路

  • 确定切分的终止条件

    直到所有的子问题都是长度为 1 的数组，停止切分。

  • 准备数据，将大问题切分为小问题

    递归地将原数组二分为左区间与右区间，直到最终的数组只剩下一个元素，将其返回

  • 处理子问题得到子结果，并合并

    • 将数组切分为左右区间

      • 对与左区间：从右到左计算左边的最大子序和
      • 对与右区间：从左到右计算右边的最大子序和

    • 由于左右区间计算累加和的方向不一致，因此，左右区间直接合并相加之后就是整个区间的和

    • 最终返回左区间的元素、右区间的元素、以及整个区间(相对子问题)和的最大值

•  c++代码实现

int maxSubArrayRec(vector &nums,int left,int right){
    if(left==right) return nums[left];

    int mid=left+(right-left)/2;
    int l=maxSubArrayRec(nums,left,mid);
    int r=maxSubArrayRec(nums,mid+1,right);

    int leftsub=nums[mid],rightsub=nums[mid+1];
    int lefttmp=leftsub,righttmp=rightsub;
    for(int i=mid-1;i>=left;--i){
        lefttmp+=nums[i];
        leftsub=max(lefttmp,leftsub);
    }
    for(int j=mid+2;j<=right;++j){
        righttmp+=nums[j];
        rightsub=max(rightsub,righttmp);
    }

    int sum=INT_MIN;
    sum=max(l,sum);
    sum=max(r,sum);
    sum=max(leftsub+rightsub,sum);

    return sum;
}


int maxSubArray(vector& nums) {
    return maxSubArrayRec(nums,0,nums.size()-1);
}

50. Pow(x, n) 

题目描述

实现 pow(x, n) ，即计算 x 的 n 次幂函数。

示例 1:

输入: 2.00000, 10
输出: 1024.00000

示例 2:

输入: 2.10000, 3
输出: 9.26100

示例 3:

输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25

• 解题思路

  • 确定切分的终止条件

    对n不断除以2，并更新n，直到为0，终止切分

  • 准备数据，将大问题切分为小问题

    对n不断除以2，更新

  • 处理子问题得到子结果，并合并

    • x与自身相乘更新x
    • 如果n%2 ==1
      • 将p乘以x之后赋值给p(初始值为1)，返回p

  • 最终返回p

•  c++代码实现

double myPow(double x, int n) {
    long long N=n;
    //确定不断切分的终止条件
    if(N==0) return 1;
    //处理n为负的情况
    if(N<0){
        x=1/x;
        N=-N;
    }

    //准备数据，并将大问题拆分为小的问题
    long double m=myPow(x,N/2);
    if(N%2==0) return m*m;
    else return m*m*x;
}

参考链接：

https://leetcode-cn.com/tag/divide-and-conquer/
https://github.com/datawhalechina/team-learning-program/blob/master/LeetCodeClassification/1.%E5%88%86%E6%B2%BB.md#%E5%88%86%E6%B2%BB%E7%AE%97%E6%B3%95%E7%9A%84%E6%AD%A5%E9%AA%A4

分治算法总结