08年A题数码相机定位学习笔记

To Be Continue…

数码相机定位学习笔记

世界坐标系

相机坐标系

图像物理坐标系

像素坐标系

问题重述

关于确定两部相机的相对位置的相机系统标定问题，描述为：设计标靶，取1个边长为100mm的正方形，分别以四个顶点(对应为A、C、D、E)为圆心，12mm为半径作圆。以AC边上距离A点30mm处的B为圆心，12mm为半径作圆，要求：

1. 建立数学模型和算法以确定靶标上圆的圆心在该相机像平面的像坐标, 这里坐标系原点取在该相机的光学中心，x-y平面平行于像平面;
2. 对由图2、图3分别给出的靶标及其像，计算靶标上圆的圆心在像平面上的像坐标, 该相机的像距(即光学中心到像平面的距离)是1577个像素单位(1毫米约为3.78个像素单位)，相机分辨率为1024×768;
3. 设计一种方法检验你们的模型，并对方法的精度和稳定性进行讨论;
4. 建立用此靶标给出两部固定相机相对位置的数学模型和方法.

---

一、摘要

本文研究数码相机的标定问题，在了解相机成像模型的前提下，对靶标的像用Matlab和python进行处理，得到靶标上五个圆圆心的像坐标。再利用坐标系间的转换结合python解方程由圆心的像坐标解出相机坐标系到世界坐标系之间的旋转变换$R$和平移变换$T$，由此确定每部相机及其光轴对世界坐标系的相对位置，进而得到两台相机的相对位置。

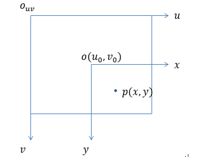
本文牵涉到坐标系的转换，因此首先为整个系统建立如下坐标系：以靶标为参照物的世界坐标系，以相机光学中心为原点的相机坐标系、像平面物理坐标系和像平面像素坐标系。

对于第一个问题，我们运用同侧外公切线法求各圆圆心像素坐标的模型，即对于两个等大的圆作外公切线，其中任何一个圆的圆心都在该圆上两个切点的连线上，该圆圆心在像平面上的像也在两切点的像的连线上。作两组切点的像的连线，其交点即为圆心。根据圆心的像素坐标，可求出圆心在相机坐标系中的物理坐标。在求解切线的时候，本文使用Matlab首先进行图像处理，得到其像素轮廓，然后用python在不同的圆两两之间寻找公切线，得到切点，进而得到圆心。·

在第二问中，我们根据第一问中提出的模型以及靶标的像(图三)求出了五个圆圆心的像坐标(像素坐标)：A(322.24,193.44)，B(419.67,195.65)，C(630.89,200.45)，D(288.51,501.96)，E(591.66,497.00)。又因为根据第一问得待求参数只有六个了，所以还需要一个点及其像坐标，即为 F(470.67,197.32)可以取圆A和圆C的内公切线的交点，由高等几何的知识，共线三点保持简单比不变等性质，得到含六个方程的线性方程组，进而解出外参数。

第三问中，我们考虑模型的精度和稳定性。通过比较成像前后的交比(前：1.290,后：1.30)基本不变，该模型具有较好的准确性与稳定性。但是本身有一些客观因素会造成精度的偏差比如相机在获取图像时就存在精度上的偏差，再者由于像素点为离散点，模型中求出来的不是准确切线，只有在像的大小合适的情况下才能保证精度。至于稳定性，则跟所给靶标圆的半径有关。

第四问中，本文根据针孔摄像机模型以及靶标的几何形状和大小，求出靶标各圆心在相机坐标系的坐标，用同样的方法求出靶标在另一个相机坐标系中的坐标。根据相机坐标系与世界坐标系之间的转换关系，代入靶标中各圆心在相机坐标系和世界坐标系中的坐标，用Matlab解非线性方程组可计算出两个相机坐标系的变换关系，包括旋转矩阵R 和平移矩阵T。由于每部相机及其光轴对世界坐标系的相对位置已经确定，所以两部相机的相对位置就确定了。

---

二、问题分析

> 模型假设

1. 物点、光心和像点这三点在同一条直线;
2. 不考虑大气因素对成像的影响;
3. 不考虑由镜片引起的畸变;
4. 数码相机中沿长宽方向的焦距相等;
5. 数码相机的光轴垂直于像平面;
6. 焦距远小于物距，可近似等于像距;
7. 题目所给的图像以及数据是精确的.

---

> 建模准备

由透镜的成像原理，有
$$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$$

其中，$f$为透镜的焦距，$u$为物距，$v$为像距。

物体在摄像机成像原理可知，一般地有$u\gg f$，于是$v=f$，这时可将透镜成像原理近似地由小孔成像原理代替，所以可以用物体在投影平面的像代替物体在像平面的像。

空间任何一点P在图像上的成像位置可以用针孔模型近似表示，即任何点P在图像上的投影位置P’，为光心O与P点的连线OP与图像平面坐标系的交点。这种关系也称为中心射影或透视投影。

---

> 问题分析

• 对于第一问，需要确定靶标的上圆的圆心在相机像平面中的像坐标，由于相机在成像时图像发生畸变，所以在像平面上的像不是规则图形。由小孔成像模型知道，物坐标和像坐标之间成比例关系。因此建立世界坐标系，确定世界坐标系与像坐标系的关系是解决第一问的关键。进而确定旋转矩阵$R$ 和平移变换$T$，得出世界坐标系到像素坐标的变换矩阵。

• 对于第二问，本题给的靶标是圆，不能利用边缘抽取的方法或霍夫变换的方法来提取边缘点数据。注意到，在针孔模型下，由于射影变换的不变性，直线的像仍然是直线。另一方面，对两等圆的外公切线，同一圆上的两切点连线过圆心，所以圆心的像就在两组切点像的连线上。于是通过求出两组外公切线的切点连线的交点来求圆心。对于求切线的方法，由于图像的轮廓为离散的像素点，所以采用限定范围后寻找最接近切点的像素点的方法求出切线。可以用matlab利用Canny边缘检测法得到图形的轮廓(边缘点信息)，并用python求出两组外公切线，得到切点坐标，进而求出像圆心的像素坐标。

• 在第三问中我们需要设计一种方法来检验模型的可靠性，并分析此方法的精度和稳定性。对此通过比较靶标中圆的圆心在投影矩阵M作用下得到的像圆心和拍摄得到的椭圆的几何中心对比，以检验我们的模型。在模型的稳定性上，由于像的轮廓为离散点，所以求出的切线是有偏差的，当像尺寸过小时，相对偏差会增大。另一方面，当像过大的时候，轮廓可能出现并排的很多像素点，导致找到的切线相对误差变大。通过扰动靶标中圆，并对其像图中椭圆发生的变化进行比较分析，以判断此检验方法的稳定性，并求出精度。

• 在第四问中考虑二个相机的相互关系时，可以由问题一的投影矩阵$M$，得到照相机的外部参数，即它对于世界坐标系的方位。在同一世界坐标系下，再由两个照相机的像图分别求出他们的方位，这样就可确定这两个相机的相对位置。

---

> 符号说明

$O_i$：圆$i$的圆心的像

${\pi }_n$：圆$n$的像轮廓

$P_i^{(n)}(x_i^{(n)},y_i^{(n)})$：${\pi }_n$上的点

$E_n$：$P_i^{(n)}(x_i^{(n)},y_i^n)$全体构成的集合

$A^{\prime }$、$B^{\prime }$、$C^{\prime }$、$D^{\prime }$、$E^{\prime }$：标靶上的五个原的圆心

$F^{\prime }$：像圆$A$、$C$的内公切线的像交点

$R$：旋转矩阵

$T$：平移矩阵

$M$：世界坐标系到像素坐标系的变换矩阵

三、刚体变换

刚体是由一群数量超多的质点组成。实际而言，不可能精确地追踪其中每一个质点的运动。为了简化运算，可以利用刚体的"刚性"，即其内部所有质点彼此之间距离不变的性质。

---

• 绕Z轴逆时针旋转$\alpha$，坐标变换之间的关系

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}\cos \alpha & \sin \alpha & 0\\ -\sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right]\text{\hspace{1em}(i)}$$

• 绕y轴逆时针旋转$\beta$，坐标变换之间的关系

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}\cos \beta & 0& -\sin \beta \\ 0& 1& 0\\ \sin \beta & 0& \cos \beta \end{array}\right]\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right]\text{\hspace{1em}(ii)}$$

• 绕x轴逆时针旋转$\gamma$，坐标变换之间的关系

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \gamma & \sin \gamma \\ 0& -\sin \gamma & \cos \gamma \end{array}\right]\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right]\text{\hspace{1em}(iii)}$$

---

不妨设其中绕x、y、z的旋转矩阵分别为R1、R2、R3，则有
$$R=R_1{R}_2{R}_3\text{\hspace{1em}(iv)}$$

这就是世界坐标系到相机坐标系的旋转矩阵。

---

3.1世界坐标系$\to$相机坐标系

图1 世界坐标➡相机坐标

假设在世界坐标系中物体的位置坐标为$(X_w,Y_w,Z_w{)}^T$，相机坐标系中的坐标为$(X_c,Y_c,Z_c{)}^T$，则联系两个坐标系的旋转变换关系为
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]$$再加上平移矩阵$T=(T_0,T_1,T_2)$，既得两个坐标系的变换关系为
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=R\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+T^{\prime }$$写成矩阵乘积的形式如下
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cc}R& T^{\prime }\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\text{\hspace{1em}(v)}$$

其中，$0$是$1\times 3$的行向量。

3.2相机坐标系$\to$图像物理坐标系

图2 相机坐标➡物理坐标

相机坐标系到图像物理坐标系的转换是基于相似投影变换，也即位似变换，物体在相机坐标系中的坐标为$(X_c,Y_c,Z_c{)}^T$，物体在图像物理坐标系的坐标为$(x,y{)}^T$，根据相似关系我们易得如下关系式
$$\frac{Z_c}{f}=\frac{Y_c}{y}=\frac{X_c}{x}$$即得
$$\begin{array}{r}\{\begin{array}{l}x=\frac{X_c}{Z_c}f\\ y=\frac{Y_c}{Z_c}f\end{array}\end{array}$$同样，我们可以写成矩阵相乘形式如下
$$Z_c\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]\text{\hspace{1em}(vi)}$$

其中$f$是相机的焦距。

3.3图像物理坐标系$\to$像素坐标系(离散)

图3 物理坐标➡像素坐标

因为像素坐标系是一系列离散的点，我们可以根据比例关系，物体在图像物理坐标系的坐标为$(x,y{)}^T$，在像素坐标系的坐标为$(u,v{)}^T$，根据对应成比例即得如下关系
$$\begin{array}{r}\{\begin{array}{l}u=\frac{x}{\mathrm{d}x}+u_0\\ v=\frac{y}{\mathrm{d}y}+v_0\end{array}\end{array}$$写成矩阵相乘形式如下
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}1/\mathrm{d}x& 0& u_0\\ 0& 1/\mathrm{d}y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\text{\hspace{1em}(vii)}$$

其中，$\mathrm{d}x$、$\mathrm{d}y$分别表示每个像素在x、y方向上的物理尺寸。

3.4世界坐标系$\to$像素坐标系

图4 世界坐标系➡像素坐标系

联立上述(v)、(vi)、(vii)式，即得
$$Z_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}1/\mathrm{d}x& 0& u_0\\ 0& 1/\mathrm{d}y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& T^{\prime }\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$为了描述的方便，我们令
$$\left[\begin{array}{ccc}1/\mathrm{d}x& 0& u_0\\ 0& 1/\mathrm{d}y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]=\left[\begin{array}{cccc}{f}_x& 0& u_0& 0\\ 0& f_y& v_0& 0\\ 0& 0& 1& 0\end{array}\right]=M_1$$

其中，$f_x=f/\mathrm{d}x$，$f_y=1/\mathrm{d}y$

同理，令
$$\left[\begin{array}{cc}R& T^{\prime }\\ 0& 1\end{array}\right]=M_2$$则世界坐标系到像素坐标系的坐标转换关系可以表示为
$$Z_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=M\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\text{\hspace{1em}(viii)}$$

其中，$M=M_1{M}_2$，$M$是$3\times 4$的矩阵。

不妨记
$$M=\left[\begin{array}{cccc}{m}_{11}& m_{12}& m_{13}& m_{14}\\ m_{21}& m_{22}& m_{23}& m_{24}\\ m_{31}& m_{32}& m_{33}& m_{34}\end{array}\right]$$写成线性方程组的形式如下
$$\begin{array}{r}\{\begin{array}{l}{Z}_{c}u=m_{11}{X}_w+m_{12}{Y}_w+m_{13}{Z}_w+m_{14}\\ \\ Z_{c}v=m_{21}{X}_w+m_{22}{Y}_w+m_{23}{Z}_w+m_{24}\\ \\ Z_c=m_{31}{X}_w+m_{32}{Y}_w+m_{33}{Z}_w+m_{34}\end{array}\end{array}$$从中消去$Z_c$得
$$\begin{array}{r}\{\begin{array}{l}u=\frac{m_{11}{X}_w+m_{12}{Y}_w+m_{13}{Z}_w+m_{14}}{m_{31}{X}_w+m_{32}{Y}_w+m_{33}{Z}_w+m_{34}}\\ \\ v=\frac{m_{21}{X}_w+m_{22}{Y}_w+m_{23}{Z}_w+m_{24}}{m_{31}{X}_w+m_{32}{Y}_w+m_{33}{Z}_w+m_{34}}\end{array}\end{array}$$又因为旋转变换的矩阵是正交矩阵，所以还有约束条件
$$\begin{array}{r}\{\begin{array}{l}{r}_{11}^2+r_{12}^2+r_{13}^2=1\\ r_{12}^2+r_{22}^2+r_{23}^2=1\\ r_{13}^2+r_{32}^2+r_{33}^2=1\end{array}\end{array}$$

代入上述格式，只需要求解6个外参数，问题只给出5个标靶点(5个方程)，所以还需要一个方程，根据射影变换的不变性质，不妨取圆A和圆C的内公切线的连线交点与其像的关系为第6个方程，即可求解6个外部参数。

利用标靶上已知点与它们的像坐标之间的转换关系，我们可以求出$M$矩阵的各参数的值，从而确定出给定相机中物体的像坐标，我们可以根据$M$矩阵求出物体在世界坐标系的方位，从而可以确定出在世界坐标系的两部位置不同的相机之间的相对位置。

四、射影变换

射影变换保持共线三点仍为共线的点及简单比不变，利用圆的外公切线的性质求得像坐标，并将其转换为图像物理坐标，利用MATLAB求解得圆心在像平面的坐标，根据相机的内参数矩阵求得，再利用高等代数的知识求得外参数。

性质1：直线经小孔后所得到的像仍为直线.

证：过相异两点有且仅有一条直线，根据平面对偶原则，如果两个三点形的对应顶点连线共点，则其对应边的交点必定共线。由上图，任取物平面$\alpha$上直线AB上一点P，则经小孔O后在像平面$\beta$的成像点为P'，易知P'同时在平面OAB和平面$\beta$上，所以P'也在两平面的交线A'B'上，所以直线经小孔后所得到的像仍为直线。

性质2：两直线交点的像仍为两直线像的交点.

证：据Desargues finite geometry，设物平面$\alpha$上任意两直线AB、CD经小孔O在像平面$\beta$上所成像直线为A'B'、C'D'，任取直线AB上一点E，则据性质1易知，点E'同时在平面ABB'A'、平面CDD'C'和平面$\beta$上，即E'同时在直线A'B'和直线C'D'上，也即两直线交点的像仍为两直线像的交点。容易将其推广到曲线相交的情况。

性质3：物圆的某一条切线及圆的切点的像，该切线仍为像平面的一条直线，并且像切点即为物圆的切点.

证：易知物圆O与其切线的交点K仍为像圆Γ与像直线的交点。又因为物圆与切线l相切于一点，所以据性质2，像圆Γ'(椭圆)与像直线l'至少有一个交点。假设物圆的切线不是像圆的切线，即像圆与该像直线交于两点A'、B'。根据光路可逆原理，将像平面$\beta$的的像投在物平面$ \alpha $上，则直线l'与曲线Γ'的两交点在物平面的像A、B即为直线l与曲线Γ的交点，与曲线Γ与直线l相切与一点K矛盾，故假设不成立，所以，切线即为像圆的切线，并且物圆切点的像即为像切线与像圆Γ'的切点。

利用最小二乘法拟合得椭圆的方程，并求得椭圆的中心，同圆心的像中心做方差分析，得到精确度的评价标准。

问题四：利用世界坐标系中两部位置固定的相机摄的像，代入世界坐标系与图像坐标系的转换矩阵M，列出方程，即可得出两部相机在世界坐标系的相对位置关系。

---

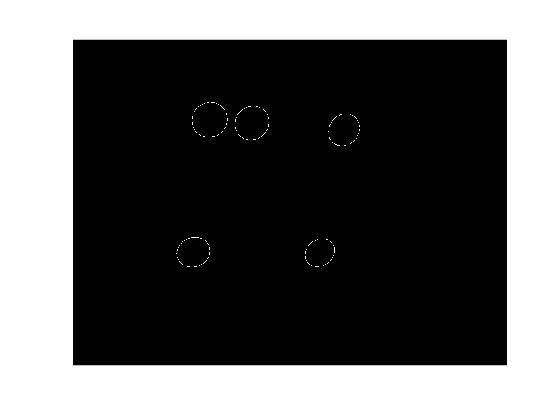
• 首先我们需要进行灰度处理，再利用Canny边缘检测算法得到边缘像素点的坐标

图5 灰度图

clear
clc
%读取RGB格式的图像
YuanPic=imread('picture1.jpg');
%RGB到灰度图像的转换
FirstGrayPic=rgb2gray(YuanPic);
%原来图像的矩阵的参数
[rows,cols,colors]=size(YuanPic);
%参数创建一个全零的矩阵
MidGrayPic=zeros(rows,cols);
%创建的全零矩阵转化为uint8格式
MidGrayPic=uint8(MidGrayPic);
for i=1:rows
    for j=1:cols
        sum=0;
        for k=1:colors
            %进行转化的关键公式
            sum=sum+YuanPic(i,j,k)/3;
        end
        MidGrayPic(i,j)=sum;
    end
end
imwrite(MidGrayPic,'pic/DarkMouseGray.png','png');
%显示原来的RGB图像
figure(1);
imshow(YuanPic,'InitialMagnification','fit');
%显示经过函数运算后的灰度图像
figure(2);
imshow(FirstGrayPic,'InitialMagnification','fit');
%显示转化之后的灰度图像
figure(3);
imshow(MidGrayPic,'InitialMagnification','fit');

• 再利用Canny算子提取边缘点的信息

图6 边缘图

clear
clc
rgb=imread('picture1.jpg');
I=rgb2gray(rgb);
Edge=edge(I,'Canny',0.35);
figure(2);
imshow(Edge,'InitialMagnification','fit');
hold on;

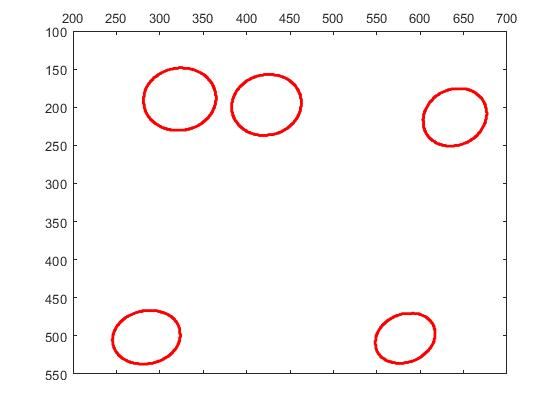
• 画出边缘点的离散图

图7 边缘点离散图

clear
clc
rgb=imread('picture1.jpg');
I=rgb2gray(rgb);
Edge=edge(I,'Canny',0.35);
[x,y]=find(Edge');
% 旋转坐标轴变换
% a=y;b=x;
% y=b;x=a;
figure(3);
for i=1:1309
   plot(x(i),y(i),'.r');
   hold on;
end
set(gca,'YDir','reverse'); 
set(gca,'XAxisLocation','top'); 

五、模型求解

> 外公切线法求像素平面的圆心坐标

---

虽然物体在数码相机成像的过程中会发生形状畸变，但是仍可以找到一些保持不变的性质。根据高等几何知识，共线三点的像仍保持线段的简单比不变等性质，如曲线的切点，其像仍为曲线的切点；曲线的交点仍为像曲线的交点。本题中求解像平面中圆心的坐标，利用了“任意两靶标的同侧公切线的切点，其像的连线仍为所成像图形的同侧公切线”和“圆心的像在平行切线切点的像的连线上”两个不变性质。具体求像平面圆心坐标步骤如下:

1. 对每一个标靶中圆的像，求两组其与其他圆的像的上下/左右外公切线的交点。对如下图所示的圆A，可选取如下所示两组切线来求切点P1、P2、P3和P4；

图8 求像圆心示意图

2. 利用求出的两组切点求圆心的像。如上图连接P1、P2和P3、P4，则圆心的像即为两条直线P1P2和P3P4的交点。

对圆心的像的求解将借助MATLAB软件来实现。首先使用imread()函数将题中所给的靶标的像输入至MATLAB中，再将其转化为二值图。由于求圆心的像的坐标仅与像的边界点有关，因此需要剔除像内部的点，提取图像的轮廓。提取图像轮廓可以采用Canny边缘检测算法来实现。

---

虽然图形的切线与图形的交点理论上只有一个，但是由于像是由像素单位构成的，而像素单位是离散的。因此像的轮廓并不光滑，真正的切点有可能没有被包含。故在这种情况下，退而求其次，求最佳的像素点。显然，一条公切线上的两个最佳点应满足这两个圆的像轮廓上的所有其他像素点都在这两个最佳点连线的同侧，这时，我们便认为最佳点即为切点。求解算法如下：

• 首先在两个像曲线${\pi }_1$、${\pi }_2$上粗略地确定切点所在的大致范围，然后分别提取范围内的所有点$P_i^{(1)}(x_i^{(1)},y_i^{(1)})$，$P_j^{(2)}(x_j^{(2)},y_j^{(2)})$，$i,j=1,2,\cdots ,n$，其集合为$E_1$、$E_2$
• 在集合$E_1$、$E_2$中任取$P_i^{(1)}$、$P_j^{(2)}$，连接两点的直线，求出其直线方程为

$$y=\frac{y_i^{(1)}-y_j^{(2)}}{x_i^{(1)}-x_j^{(2)}}x+\frac{x_i^{(1)}{y}_j^{(2)}-x_j^{(2)}{y}_i^{(1)}}{x_i^{(1)}-x_j^{(2)}}$$

• 将集合$E_1$、$E_2$中所有其他的元素代入上述直线方程，若结果均为$y>\frac{y_i^{(1)}-y_j^{(2)}}{x_i^{(1)}-x_j^{(2)}}x+\frac{x_i^{(1)}{y}_j^{(2)}-x_j^{(2)}{y}_i^{(1)}}{x_i^{(1)}-x_j^{(2)}}$或$y<\frac{y_i^{(1)}-y_j^{(2)}}{x_i^{(1)}-x_j^{(2)}}x+\frac{x_i^{(1)}{y}_j^{(2)}-x_j^{(2)}{y}_i^{(1)}}{x_i^{(1)}-x_j^{(2)}}$，则说明其他所有元素均在直线的同侧，则$P_i^{(1)}$、$P_j^{(2)}$即为所求的最佳外公切线的切点。若结果不均在同一侧，返回步骤二

重复以上操作直至遍历$E_1$、$E_2$中所有元素。

表1 最佳切点的像素坐标

	上(左)公切线坐标	下(右)公切线坐标
$A$,​ $B$	(326,148) (429,156)	(324,230) (418,237)
$E$, $D$	(295,466) (597,470)	(282,538) (584,536)
$B$, $E$	(386,182) (248,491)	(460,212) (322,511)
$E$, $C$	(261,475) (619,184)	(309,528) (661,242)
$A$, $E$	(281,187) (245,505)	(365,191) (324,501)
$C$, $D$	(604,218) (549,502)	(676,213) (616,508)

得到最佳切点的坐标后，通过python求解圆心坐标

'''以圆A为例计算像圆心'''
a=[{'x': 326.0, 'y': 148.0}, {'x': 429.0, 'y': 156.0}]
b=[{'x': 324.0, 'y': 230.0}, {'x': 418.0, 'y': 237.0}]
c=[{'x': 281.0, 'y': 187.0}, {'x': 245.0, 'y': 505.0}]
d=[{'x': 365.0, 'y': 191.0}, {'x': 324.0, 'y': 501.0}]
a1=a[0];b1=b[0];c1=c[0];d1=d[0]
k1=(a1["y"]-b1["y"])/(a1["x"]-b1["x"])
k2=(c1["y"]-d1["y"])/(c1["x"]-d1["x"])
b1=(a1["x"]*b1["y"]-b1["x"]*a1["y"])/(a1["x"]-b1["x"])
b2=(c1["x"]*d1["y"]-d1["x"]*c1["y"])/(c1["x"]-d1["x"])
x=-(b1-b2)/(k1-k2)
y=(k1*b2-k2*b1)/(k1-k2)
print("x=",end='');print(x)
print("y=",end='');print(y)

> 求解结果

---

通过以上算法可计算出每个像圆的不同两组与其他像圆的上下/左右外公切线的切点，从而可以得到每个圆心的像素平面坐标。

运用python编写求解像素图中两圆的外公切线交点，进而求出像圆的圆心；再根据求得的图像边缘点坐标，拟合椭圆，求出五个椭圆的标准方程，得到五个椭圆几何中心，观察发现，像图的几何中心一般不是标靶圆的像圆心，分析两者的误差，通过扰动标靶圆的位置，得出该模型的精度与稳定性。

表2 圆心的像素坐标

标靶的点	像素平面坐标
$O_A$	( 322.24, 193.44 )
$O_B$	( 419.67, 195.65 )
$O_C$	( 630.89, 200.45 )
$O_D$	( 591.66, 497.00 )
$O_E$	( 288.51, 501.91 )
$O_F$	( 470.67, 197.32 )

根据(vii)式，我们有
$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}\mathrm{d}x& 0& -u_0\mathrm{d}x\\ 0& \mathrm{d}y& -v_0\mathrm{d}y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$$即像素坐标与图像物理坐标(单位:mm)的转换关系如下:
$$\begin{array}{r}\{\begin{array}{l}x=(u-u_0)\mathrm{d}x\\ y=(v_0-v)\mathrm{d}y\end{array}\end{array}$$

根据题意$\mathrm{d}x=\mathrm{d}y=1/3.78$，$u_0=512$，$v_0=384$

表3 圆心的图像物理坐标

标靶的点	图像物理坐标(mm)
$O_A$	( -50.20, 50.41 )
$O_B$	( -24.42, 49.83 )
$O_C$	( 31.45, 48.56 )
$O_D$	( 21.07, -29.89 )
$O_E$	( -59.12, -31.21 )
$O_F$	( -10.93, -49.92 )

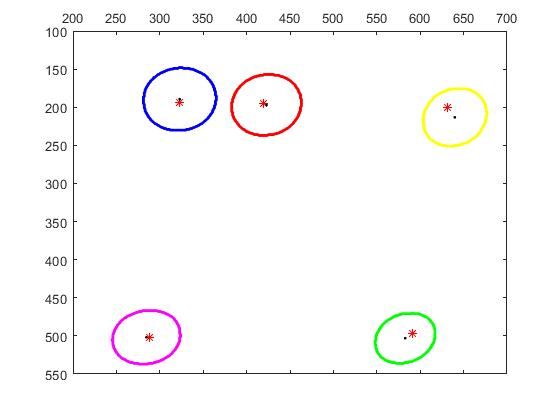
如下图所示即为原像素点、拟合椭圆方程、像圆心坐标、椭圆中心的关系:

图9 像圆心、像椭圆中心及边缘点

• python求切点

'''以圆A、B外公切线的切点为例'''
import xlrd
from queue import Queue #导入队列的模块
q=Queue(maxsize=0) #初始化空队列
stack=[]
#打开excel文件并读取数据
rbookA=xlrd.open_workbook(r'圆A.xlsx')
rbookB=xlrd.open_workbook(r'圆B.xlsx')
#sheets方法返回对象列表
rbookA.sheets()
rbookB.sheets()
#xlsx默认有3个工作簿,Sheet1,Sheet2,Sheet3
rsheetA=rbookA.sheet_by_index(0)  #取第一个工作簿
rsheetB=rbookB.sheet_by_index(0)  #取第一个工作簿
#获取行数
nrowsA=rsheetA.nrows
nrowsB=rsheetB.nrows
#存储信息的列表
a_list=[];b_list=[]
a1_list=[];b1_list=[]
a2_list=[];a3_list=[]
b2_list=[];b3_list=[]
lst1=[];LST=[]
LST2=[];lst=[]
#导入圆A边缘点信息
for i in range(nrowsA):
    dic_A={}
    x1=rsheetA.cell(i,1).value #获取x坐标
    y1=rsheetA.cell(i,0).value #获取y坐标
    dic_A["x"]=x1
    dic_A["y"]=y1
    if 320<x1<335:
        a1_list.append(dic_A)
        if y1<200:
            a2_list.append(dic_A) #上侧
        else:
            a3_list.append(dic_A) #下侧
    a_list.append(dic_A) #圆A所有的点
#导入圆B边缘点信息
for i in range(nrowsB):
    dic_B={}
    x2=rsheetB.cell(i,1).value #获取x坐标
    y2=rsheetB.cell(i,0).value #获取y坐标
    dic_B["x"]=x2
    dic_B["y"]=y2
    if 420<x2<430:
        b1_list.append(dic_B)
        if y2<200:
            b2_list.append(dic_B) #上侧
        else:
            b3_list.append(dic_B) #下侧
    b_list.append(dic_B) #圆B所有的点
#计算圆A和圆B上侧两两配对的点数
for m in range(len(a2_list)):
    for n in range(len(b2_list)):
        if a2_list[m]["x"]<b2_list[n]["x"]:
            lst0=[];dic0={};dic1={}
            dic0["x"]=a2_list[m]["x"]
            dic1["x"]=b2_list[n]["x"]
            dic0["y"]=a2_list[m]["y"]
            dic1["y"]=b2_list[n]["y"]
            lst0.append(dic0);lst0.append(dic1)
            lst1.append(lst0)        
#遍历上侧所有的点
for k in range(len(lst1)):
    q.put(lst1[k]) #写入队列
    stack.append(lst1[k])
stack2=a2_list
for i in range(len(b2_list)):
    stack2.append(b2_list[i])
for p in range(len(stack)):
    flag=1
    Q1=stack[p][0];Q2=stack[p][1]
    k1=(Q1["y"]-Q2["y"])/(Q1["x"]-Q2["x"])
    b1=(Q1["x"]*Q2["y"]-Q2["x"]*Q1["y"])/(Q1["x"]-Q2["x"])
    for r in range(len(stack2)):
        Y=k1*stack2[r]["x"]+b1
        if stack2[r]["y"]<Y: #切线上的纵坐标大于原像素值
            flag=0
            break
    if flag:
        LST.append(Q1);LST.append(Q2)
        LST2.append(LST)
print(LST2)  

• matlab绘图

clear
clc
rgb=imread('picture1.jpg');
I=rgb2gray(rgb);
BW1=edge(I,'canny');
B=BW1;K=sum(B);
k=bwboundaries(B);
E=k{1,1};plot(E(:,2),E(:,1),'.m');hold on;
A=k{2,1};plot(A(:,2),A(:,1),'.b');
B=k{3,1};plot(B(:,2),B(:,1),'.r');
D=k{4,1};plot(D(:,2),D(:,1),'.g');
C=k{5,1};plot(C(:,2),C(:,1),'.y');
set(gca,'YDir','reverse'); 
set(gca,'XAxisLocation','top'); 
hold on;plot(630.89,200.45,'*r')
plot(322.24,193.44,'*r');plot(419.67,195.65,'*r')
plot(591.66,497.00,'*r');plot(288.51,501.96,'*r')
plot(322.9129,189.4356,'.k');plot(422.921,197.0369,'.k')
plot(639.8883,213.2367,'.k');plot(582.6726,503.0003,'.k')
plot(284.6779,501.7830,'.k')

> 结果分析

通过试验，我们发现标靶圆经过变换的像图像的几何中心一般不是圆心的像坐标，通过扰动标靶圆的位置，可以分析模型精度与稳定性。

对于椭圆的标准方程
$$A{x}^2+2Bxy+C{y}^2+Dx+Ey+F=0$$
可以将之转化为
$$A(x-u{)}^2+2B(x-u)(y-v)+C(y-v{)}^2+F=0$$
具体步骤为，将后式的各乘积乘方项展开，根据与前式对应项系数相等的法则便可求得 $u$、$v$、$f$ 的值。其中$(u,v)$便是该椭圆的中心。即
$$\begin{array}{r}\{\begin{array}{l}u=\frac{BE-CD}{AC-B^2}\\ v=\frac{BD-AE}{AC-B^2}\end{array}\end{array}$$

即可求出像图中拟合椭圆的几何中心坐标，一般不是圆心的像坐标。

进而得到像圆拟合椭圆的标准方程如下表4所示:

表4 像素坐标系下拟合椭圆的标准方程

拟合椭圆	标准方程
椭圆$A^{\prime }$	$3.4052\ast 10^{-5}{x}^2+2.9691\ast 10^{-6}xy+3.5346\ast 10^{-5}{y}^2-2.2554\ast 10^{-2}x-1.4350\ast 10^{-2}y+4.9416=0$
椭圆$B^{\prime }$	$3.5730\ast 10^{-5}{x}^2+4.8599\ast 10^{-6}xy+3.5632\ast 10^{-5}{y}^2-3.1180\ast 10^{-2}x-1.6097\ast 10^{-2}y+8.1219=0$
椭圆$C^{\prime }$	$1.8252\ast 10^{-5}{x}^2+4.6121\ast 10^{-6}xy+1.6965\ast 10^{-5}{y}^2-2.4342\ast 10^{-2}x-1.0186\ast 10^{-2}y+8.8502=0$
椭圆$D^{\prime }$	$3.79\ast 10^{-6}{x}^2+1.4180\ast 10^{-6}xy+4.1926\ast 10^{-6}{y}^2-5.1311\ast 10^{-3}x-5.0440\ast 10^{-3}y+2.7589=0$
椭圆$E^{\prime }$	$1.3466\ast 10^{-5}{x}^2+3.0460\ast 10^{-6}xy+1.6934\ast 10^{-5}{y}^2-9.1953\ast 10^{-3}x-1.7862\ast 10^{-2}y+5.7694=0$

clear
clc
rgb=imread('picture1.jpg');
I=rgb2gray(rgb);
%用Canny算子对其进行边缘检测
BW1=edge(I,'canny');
B=BW1;K=sum(B);
k=bwboundaries(B);
E=k{1,1};
A=k{2,1};
B=k{3,1};
D=k{4,1};
C=k{5,1};
x(:,1)=E(:,2);x(:,2)=E(:,1);
F=@(p,x)p(1)*x(:,1).^2+p(2)*x(:,1).*x(:,2)+p(3)*x(:,2).^2+p(4)*x(:,1)+p(5)*x(:,2)+p(6);
p0=[1 1 1 1 1 1];
warning off
%拟合系数，最小二乘方法
p=nlinfit(x,zeros(size(x,1),1),F,p0);
plot(x(:,1),x(:,2),'ks');
hold on
xmin=min(x(:,1));
xmax=max(x(:,1));
ymin=min(x(:,2));
ymax=max(x(:,2));
ezplot(@(x,y)F(p,[x,y]),[-1+xmin,1+xmax,-1+ymin,1+ymax]);
x=(p(2)*p(5)-2*p(3)*p(4))/(4*p(1)*p(3)-p(2)^2);disp(x);
y=(p(2)*p(4)-2*p(1)*p(5))/(4*p(1)*p(3)-p(2)^2);disp(y);
set(gca,'YDir','reverse'); 
set(gca,'XAxisLocation','top'); 

六、精度与稳定性分析

> 精度分析

---

1.畸变导致误差

2.对离散的像素点进行操作会产生误差

3.模型假设误差

4.精度检验

精度检验可以转换为像上的图形与靶标上的圆的映射关系的检验。具体方法是，首先将像上的轮廓的点投射到以上模型求得的靶标上，然后计算靶标上相应的圆心距离这些点的平均距离和标准差，平均距离越贴近于靶标上圆的半径，则模型越准确；标准差越小，说明模型越准确。

---

> 稳定性分析

经检验，空间共线三点的像仍然保持共线关系且保持简单比不变。由此可见，模型具有较高的精确性与稳定性。

---

6.1预备知识

在射影变换下，保持点的直线关系及交比不变的射影不变量。

>影消点

首先，影消点的存在使得两直线的中心射影变换不构成双射(因为两平行直线没有交点)。中心射影构成双射约定如下:

1. 在每条直线上添加唯一的一个点，此点不是该直线上原有的点，称为无穷远点;
2. 相互平行的直线上添加的无穷远点相同，不平行直线上添加的无穷远点不同，即对应于平面上每一方向，有唯一无穷远点，平行的直线交于同一无穷远点；交于同一无穷远点的直线平行。

>交比

共线四点P1、P2、P3、P4的交比定义如下:
$$(P_1{P}_2,P_3{P}_4)=\frac{({\lambda }_1-{\lambda }_3)({\lambda }_2-{\lambda }_4)}{({\lambda }_2-{\lambda }_3)({\lambda }_1-{\lambda }_4)}$$

其中，P1、P2称为基点，P3、P4称为分点，且$P_i=:a+{\lambda }_{i}b$，$(i=1,2,3,4)$

即
$$(P_1{P}_2,P_3{P}_4)=\frac{P_1{P}_3\cdot P_2{P}_4}{P_2{P}_3\cdot P_1{P}_4}=\frac{\det (P_1;P_3)\cdot \det (P_2;P_4)}{\det (P_2;P_3)\cdot \det (P_1;P_4)}$$

其中，$P_i=(x_i,y_i),(i=1,2,3,4)$为齐次线性坐标，二阶行列式几何意义。

6.2模型检验

由题给条件及数据可得：A、B、C、$P_{\infty }$4点共线(其中$P_{\infty }$为直线上的无穷远点)，根据交比定义可得:
$$(AB,C{P}_{\infty })=\frac{AC}{BC}\cdot \frac{B{P}_{\infty }}{A{P}_{\infty }}=(ABC)=\frac{AC}{BC}=\frac{10}{7}=1.429$$

此时交比即为简单比，据射影变换保持共线四点的交比不变。

即应有像A'、B'、C'、P'四点共线，且$(AB,C{P}_{\infty })=(A^{\prime }{B}^{\prime },C^{\prime }{P}^{\prime })$。其中A'，B'，C'为圆心A，B，C的像点，P'为直线AC上的影消点。

---

检验步骤如下：

i) 验证A'，B'，C'三点共线；

计算可得$A^{\prime }{B}^{\prime }=(25.78,-0.58)$、$A^{\prime }{C}^{\prime }=(81.65,-1.85)$，

因为$A^{\prime }{C}^{\prime }=\lambda A^{\prime }{B}^{\prime }(\lambda \approx 3.17)$，所以A'，B'，C'三点共线。

ii) 计算直线AC像的影消点P';

根据上述约定2可得，因为$AC\parallel ED$，故A'C'与E'D'的影消点均为P'，即P'为直线A'C'与E'D'的交点，其中E'、D'为圆E、D圆心的像点。

直线A'C'的方程为:
$$y-48.56=\frac{50.41-48.56}{-50.20-31.45}(x-31.45)$$
直线E'D'的方程为:
$$y+31.21=\frac{31.21-29.89}{21.07+59.12}(x+59.12)$$
联立上述两式得影消点$P^{\prime }(2032.48,3.22)$。

iii) 计算像点A'，B'，C'，P'的交比.
$$(A^{\prime }{B}^{\prime },C^{\prime }{P}^{\prime })=\frac{\det (P_1;P_3)\cdot \det (P_2;P_4)}{\det (P_2;P_3)\cdot \det (P_1;P_4)}=1.430=(AB,C{P}_{\infty })$$

---

又因为$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(B^{\prime },C^{\prime },P^{\prime })=2$，所以A'，B'，C'，P'四点共线。

故从检验结果看出，A'，B'，C'，$P_{\infty }$的像点A'，B'，C'，P'仍然保持共线及交比不变。由此可见，该模型具有很好的精确性与稳定性。

七、相对位置

图10 两部相机相对位置示意图

由问题一求解的$M$矩阵容易根据两部两部相机的标靶的像求得两部相机在世界坐标系中的相对位置。

根据已知的像点坐标和靶标点的几何关系可以列出方程，通过求解出靶标上的点在相机坐标系中的坐标。在用同样的方法找到靶标在另一个相机坐标中的坐标后。列出靶标上五个点(6个方程)在两个相机坐标系中的坐标变换，即可求解出两个相机坐标系之间的变换矩阵。

---

如上图10，用两部相机同时摄像时，在标定中我们可以用单相机定标方法得各自相机的外参数，即$R$、$T$。不妨设$R_1$、$T_1$为相机$C_1$相对于世界坐标系的旋转矩阵和平移向量，$R_2$、$T_2$为相机$C_2$相对于世界坐标系的旋转矩阵和平移向量。从问题一中我们可以得到下述两个方程:
$$\begin{array}{r}\{\begin{array}{l}{X}_{c1}=R_1{X}_w+T_1\\ \\ X_{c2}=R_2{X}_w+T_2\end{array}\end{array}$$
消去$X_w$后得到
$$X_{c1}=R_1{R}_2^{-1}{X}_{c2}+T_1-R_1{R}_2^{-1}{T}_2$$

令$R=R_1{R}_2^{-1}$，$T=T_1-R_1{R}_2^{-1}{T}_2$，则两部相机的关系可以由$R$和$T$描述

八、参考文献

[1]李鸿燕,张学山. 基于射影变换几何不变性的数码相机双目定位模型[J]. 上海工程技术大学学报,2009,23(04):333-337.

[2]2008 全国大学生数学建模竞赛A题优秀论文

[3]Wikipedia Rigid body

[4]数码相机的定位

[5]Wikipedia Canny edge detector

[6]高等几何(第三版).周兴和,杨明升(M).科学出版社.2015.

[7]Wikipedia Desargues’s theorem

九、附录

• X.1

• X.2

• X.3