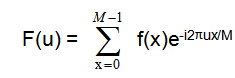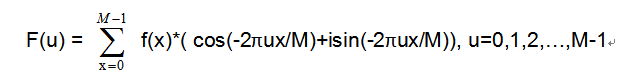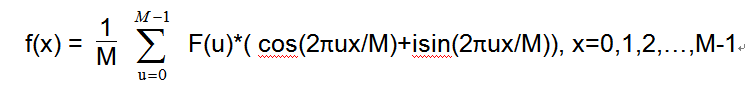C++实现一维离散傅里叶变换
本文介绍如何用C++实现一维离散傅里叶变换(Discrete Fourier Transform)。
1. 一维傅里叶变换公式简介
如果读者对傅里叶变换的认识处于一知半解的程度,那么建议先阅读相关文章,例如网络上广泛流传的《如果看了此文你还不懂傅里叶变换,那就过来掐死我吧》,以加深理解。
一维连续傅里叶变换的公式表达如下:
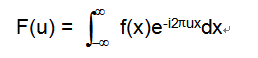
经过离散化后,上述公式变为:
其中M为x的个数,u=0,1,2,…,M-1。与连续形式的傅里叶变换相比,离散形式中e的指数多乘了一个1/M。
e -i2 πux/M可转化为三角函数cos(-2πux/M)+isin(-2πux/M),i为虚数单位。转化成三角函数形式,有利于计算机编程实现。故得到有利于编程实现的离散傅里叶变换公式如下:
观察上述离散傅里叶变换公式,不难发现,每计算一个F(u)的时间复杂度为O(N)(其中还可再细分为实数运算和复数运算,以及加法运算和乘法运算)。故算法的时间复杂度为O(N2)。对于超过50万个元素的向量,就目前的cpu运算速度而言,完成一次傅里叶变换所需要的时间是非常令人难以忍受的。而在图像处理中,一张高清图片的像素总数通常都会超过50万个。故有必要寻找一种可以快速计算傅里叶变换的算法。业界常用的快速算法叫FFT(基于蝶形分解的快速傅里叶变换)。后续将介绍如何用C++实现FFT。
对信号进行傅里叶变换,并在频域进行相关处理后,需要重建信号。这时候就需要进行离散傅里叶逆变换。离散傅里叶逆变换的公式如下:
我们将在代码中一并实现离散傅里叶逆变换。
2. 频域幅值的意义
很多刚接触傅里叶变换的人不了解频域图中的坐标和幅值的具体意义是什么。为了更好地理解傅里叶变换算法,这里有必要简短介绍一下频域图中的坐标和幅值的意义。
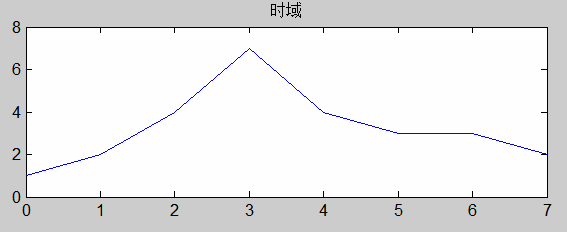
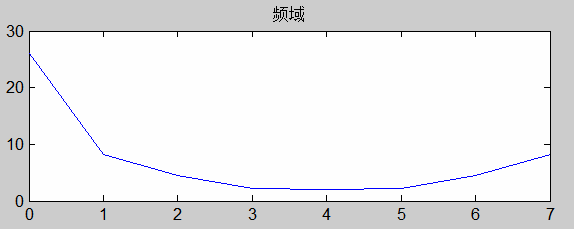
假设有一个一维信号为[1 2 4 7 4 3 3 2],在Matlab中对其进行傅里叶变换,得到求模后的变换结果为[26.0000 8.1922 4.4721 2.2107 2.0000 2.2107 4.4721 8.1922]。
通过Matlab分别作时域和频域的图形如下:频域图上的横坐标共有8个点,从低到高分别对应8个频率。其中,频率为0的点对应的幅值为26,它是傅立叶变换的直流分量,是一维信号向量所有信号值的总和。频率为1的点的幅值,则等于以下两者构成的复数的模:一维信号对实数轴余弦函数cos(-2πx*1/M)在定义域x∈0,1,2,3,...,M-1上的波形的符合程度(数值上表现为计算相关);一维信号对复数轴余弦函数sin(-2πx*1/M)在定义域x∈0,1,2,3,...,M-1上的波形的符合程度(数值上表现为计算相关)。频率为2的点的幅值,则等于以下两者构成的复数的模:一维信号对实数轴余弦函数cos(-2πx*2/M)在定义域x∈0,1,2,3,...,M-1上的波形的符合程度(数值上表现为计算相关);一维信号对复数轴余弦函数sin(-2πx*2/M)在定义域x∈0,1,2,3,...,M-1上的波形的符合程度(数值上表现为计算相关)。以此类推。
因此,某点频率的幅值,代表了原始信号的变化趋势与该频率的波形的符合程度(即相关度),信号的变化趋势越符合该频率的波形,则该频率在频域图上对应的点的幅值越大。换句话说,频率的幅值越大,则该频率在原始信号中体现出来的存在感越强;幅值越小,存在感越弱;幅值为零?不存在的。如果原始信号变化平缓,则频域图上的能量就会几乎全部集中在低频段;如果原始信号变化剧烈,则能量在中高频段也会有一定比例的分布,如上述例图(由于傅立叶变换的结果具有对称性,在上述频域图中,转移中心后,点4为最高频,点3为次高频,点2为中频)。
对于二维灰度图像,由于大多数区域的灰度过渡都是比较平缓的(只有边缘变化剧烈),故图像频谱能量主要集中在低频段。
思维拓展:当我们进行图像卷积滤波操作的时候,实际上相当于事先构造某个形状的波形,然后将图像与该波形进行卷积,卷积的结果就是图片上各个局部区域与该波形的符合程度(相关),相关值越大,表明该区域越符合该波形的形状,基于此,可以作进一步的图像处理。这个思路也同样适用于小波变换。3. C++实现
现在,我们根据前面给出的离散傅里叶变换公式,用C++来实现离散傅里叶变换(DFT):观察上式,对于给定的一维信号f(x),我们只需要用两次for循环就可以计算出傅里叶变换的结果,时间复杂度为O(N2)。
由于涉及复数运算,我们可以先定义一个复数类,并实现复数运算。
(注:编译环境是VS2013,使用MFC对话框框架)
ComplexNumber.h
#pragma once
class CComplexNumber
{
public:
CComplexNumber(double rl, double im);
CComplexNumber(void);
~CComplexNumber(void);
public:
// 重载四则运算符号
inline CComplexNumber CComplexNumber::operator +(const CComplexNumber &c) {
return CComplexNumber(m_rl + c.m_rl, m_im + c.m_im);
}
inline CComplexNumber CComplexNumber::operator -(const CComplexNumber &c) {
return CComplexNumber(m_rl - c.m_rl, m_im - c.m_im);
}
inline CComplexNumber CComplexNumber::operator *(const CComplexNumber &c) {
return CComplexNumber(m_rl*c.m_rl - m_im*c.m_im, m_im*c.m_rl + m_rl*c.m_im);
}
inline CComplexNumber CComplexNumber::operator /(const CComplexNumber &c) {
if ((0==c.m_rl) && (0==c.m_im)) {
OutputDebugStringA("11111 ComplexNumber ERROR: divider is 0!");
return CComplexNumber(m_rl, m_im);
}
return CComplexNumber((m_rl*c.m_rl + m_im*c.m_im) / (c.m_rl*c.m_rl + c.m_im*c.m_im),
(m_im*c.m_rl - m_rl*c.m_im) / (c.m_rl*c.m_rl + c.m_im*c.m_im));
}
void SetValue(double rl, double im);
public:
double m_rl; // 实部, real part
double m_im; // 虚部, imagery part
};#include "StdAfx.h"
#include "ComplexNumber.h"
CComplexNumber::CComplexNumber(void)
{
m_rl = 0;
m_im = 0;
}
CComplexNumber::CComplexNumber(double rl, double im)
{
m_rl = rl;
m_im = im;
}
CComplexNumber::~CComplexNumber(void)
{
}
void CComplexNumber::SetValue(double rl, double im) {
m_rl = rl;
m_im = im;
}完成了复数类的定义,现在我们就可以着手写离散傅里叶变换DFT的实现:
Dft1.h
#pragma once
#include "ComplexNumber.h"
#define MAX_VECTOR_SIZE 2048 // 原始信号最大允许长度
#define PI 3.141592653 // 圆周率π的近似值
class CDft1
{
public:
CDft1(void);
~CDft1(void);
public:
bool dft(double IN const vec[], int IN const len); // 一维离散傅里叶变换
bool idft(LPVOID OUT *pVec, int OUT *ilen); // 一维离散傅里叶逆变换
bool has_dft_vector(); // 是否已存有变换结果
void clear_dft_vector(); // 清除已有的变换结果
void print(); // 打印变换结果
public:
CComplexNumber *m_dft_vector; // 保存变换结果的容器
private:
bool m_has_dft_vector;
int m_dft_vector_size; // 变换结果的长度
};Dft1.cpp
#include "StdAfx.h"
#include "Dft1.h"
CDft1::CDft1(void)
{
m_dft_vector = NULL;
m_has_dft_vector = false;
m_dft_vector_size = 0;
}
CDft1::~CDft1(void)
{
if (m_has_dft_vector && (NULL != m_dft_vector) && (m_dft_vector_size>0))
delete[] m_dft_vector;
}
bool CDft1::has_dft_vector()
{
return m_has_dft_vector;
}
void CDft1::clear_dft_vector()
{
if (m_has_dft_vector && (NULL != m_dft_vector) && (m_dft_vector_size>0)) {
delete[] m_dft_vector;
m_has_dft_vector = false;
m_dft_vector_size = 0;
}
}
void CDft1::print()
{
char msg[256] = "11111 ";
if ((!m_has_dft_vector) || (NULL == m_dft_vector) || (m_dft_vector_size <= 0))
return;
for (int i = 0; i至此,我们已经用C++实现了一维离散傅里叶变换。
现在,我们编写并运行一个测试线程,验证上述代码。DWORD WINAPI test(LPVOID lParam)
{
char msg[256] = "11111 ";
double signal[] = { 15, 32, 9, 222, 18, 151, 5, 7, 56, 233, 56, 121, 235, 89, 98, 111 };
int len = sizeof(signal) / sizeof(double);
// 对一维信号进行傅里叶变换,并打印变换结果
CDft1 dft;
dft.dft(signal, len);
OutputDebugStringA("11111 傅里叶变换的结果为:");
dft.print();
// 进行傅里叶逆变换
LPVOID pVec = NULL;
int ilen = 0;
dft.idft(&pVec, &ilen);
// 打印逆变换的结果,以便和原始信号作对比
double *vec = (double *)pVec;
if ((ilen>0) && (NULL != vec)) {
OutputDebugStringA("11111 傅里叶逆变换的结果为:");
for (int x = 0; x在MFC对话框资源中添加一个test按钮,在按钮事件响应函数中添加:
::CreateThread(NULL, 0, test, 0, 0, NULL);
然后编译项目。编译成功后,先打开DebugView日志观察工具,再启动生成的exe,点击test按钮,可以在DebugView中看到以下日志输出:
可以看到,傅里叶逆变换的结果和原始信号完全一致。
为进一步验证算法的正确性,我们在Matlab的命令行窗口输入相同的一串原始信号进行傅里叶变换:
>> X = [15 32 9 222 18 151 5 7 56 233 56 121 235 89 98 111];>> F = fft(X);
>> F
F =
1.0e+03 *
Columns 1 through 5
1.4580 + 0.0000i -0.0832 + 0.2821i -0.3234 - 0.1388i -0.1467 + 0.2262i 0.1560 - 0.0440i
Columns 6 through 10
-0.0004 + 0.4622i -0.0406 - 0.2148i 0.0662 - 0.3499i -0.4740 + 0.0000i 0.0662 + 0.3499i
Columns 11 through 15
-0.0406 + 0.2148i -0.0004 - 0.4622i 0.1560 + 0.0440i -0.1467 - 0.2262i -0.3234 + 0.1388i
Column 16
-0.0832 - 0.2821i
>>
对比Matlab的傅里叶运算结果和我们的程序在DebugView中打印的变换结果,忽略四舍五入的误差,两种结果是完全一致的。
至此,我们成功地使用C++实现了一维离散傅里叶变换。
当原始信号的数量级达到几十万的时候,本文所述算法的效率将令人难以忍受。例如,信号总数N=50万时,时间复杂度为O(N2)=2500亿次运算,每一次运算还要再细分成4次左右的加法和乘法运算,也就是说,CPU大概需要进行一万亿次双精度的浮点运算。故有必要对该算法进行优化,譬如采用业界常用的蝶形分解,再赋予多线程加持。后续我们将介绍基于蝶形分解的快速傅里叶变换的C++实现。
(备注:由于傅里叶变换算法的运算过程中,每一条计算都严重依赖于上一条计算结果,故不宜采用SIMD指令集进行优化,也难以进行向量化编程)