数据结构中的树是什么？如何通过Python创建一个树？*-* Python学数据结构与算法 - 5 - 数据结构

树简介

树不同于链表和顺序表，是一种非线性的数据结构，在我们的系统中，树的结构随处可见，文件目录就是树。
树主要用来解决一对多的数据结构，其中图中橘黄色的为树，黄色的为图。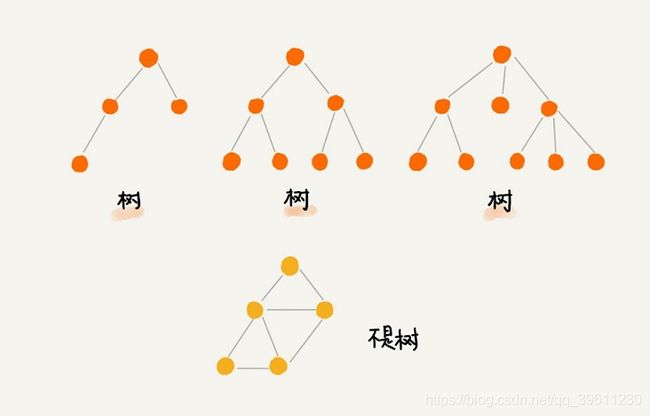

树的常用术语

结点：树中，每个结点都可以有任意数量的子节点。
根结点：没有父结点的结点称之为根结点。
父结点：除了根结点外每个结点有且只能有一个父结点。
叶子结点：没有子节点的结点称之为叶子节点。
兄弟结点：拥有相同父结点的结点互相称之为兄弟结点。

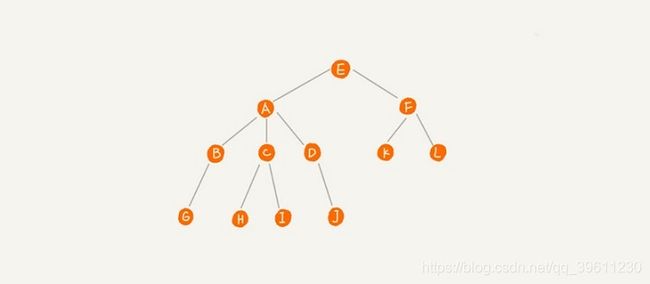
A 节点就是 B 节点的父节点，B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。我们把没有父节点的节点叫作根节点，也就是图中的节点 E。我们把没有子节点的节点叫作叶子节点或者叶节点，比如图中的 G、H、I、J、K、L 都是叶子节点。
结点的度：结点拥有的子节点数量就是度数。
树的度：树中度数最大的结点对应的度即为树的度。
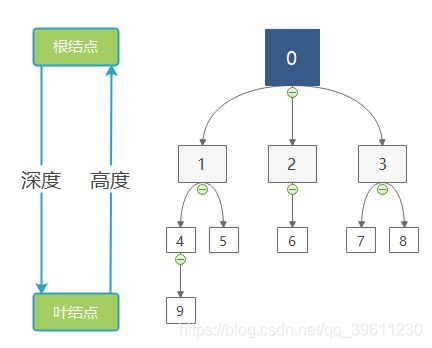
树的层数：根结点为第一层，其余结点层数为双亲结点+1。(可以从0开始计数，也可以从1开始计数，但不管是从谁开始计数，层数都不会因为计数方法的不同而改变)
树的深度：树中层数最大的结点，从根结点到子节点。
树的高度：高度和深度大小相同，但是高度是从子节点开始计算。

树的种类

树

无序树

有序树

结点之间没有任何顺序关系，可以随意交互任意结点，交换后还是相同的树。在实际场景基本没有使用。

结点之间有顺序换关系，交互结点后树发生改变。在编程中最常用的有序树是二叉树

二叉树

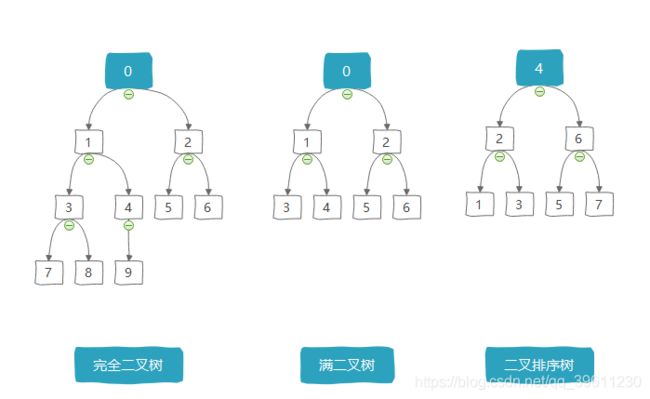
每个节点最多含有两个子树的树称为二叉树。我们列举几个常见的二叉树种类。

AVL树

二叉树

完全二叉树

满二叉树

排序二叉树

平衡二叉树

哈夫曼树

B树

……

除最后一层外其余所有层都已满的二叉树为完全二叉树，且最后一层所以结点都从左向右有序排列

所以结点都已满的的二叉树为满二叉树，因为无法添加和删除元素，满二叉树很少使用

二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树。右结点>根结点>左结点

任何节点的两棵子树的高度差不大于1的二叉树，防止排序二叉树退出成链表。

用于信息编码和压缩等技术，是带权（可以大致理解为使用次数越多权越高）路径最短的二叉树。

一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树，主要在数据库使用率较高

树的储存

顺序存储结构

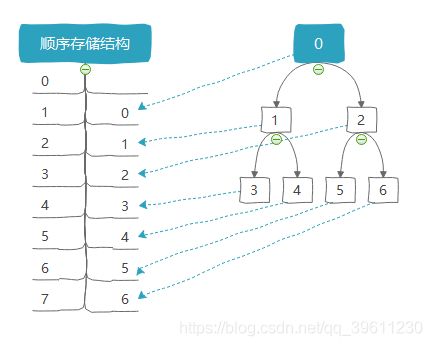
使用顺序存储结构的树虽然方便遍历，但占用空间较大，而且在增删改查上都较为麻烦，不利于操作，使用率很少，是一种非主流的二叉树。

链式存储结构

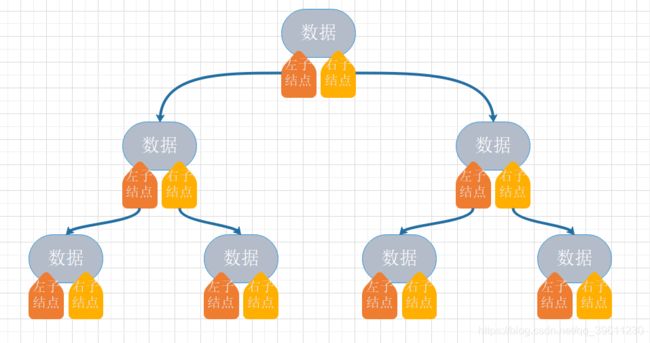
链式存储和双向链表有几分相似，只是左右结点不再是放前后链表，而是变成了左右结点。在链式存储中，我们只需获得根结点，就可以操作整个树，且方便增删改查。

用Python实现链表结构的树

这里的结点可以使用和双向链表相同的结构

创建结点

class Node:
    def __init__(self, data, left=None, right=None):
        self.data = data
        self.left = left
        self.right = right

添加结点

在添加树的叶子结点时时我们采用了队列的思维，把树同层的内容添加到队列中进行逐个寻找。

class Tree:

    def __init__(self, root=None):
        self.__root = root

    def add(self, elem):
        """创建一个新分支"""
        # 创建结点
        new = Node(elem)
        # 判断是否为空树
        if self.__root is None:
            self.__root = new
            print('头结点执行了')
        else:
            # 用来存放(deposit)节点的数组
            deposit = [self.__root]
            # 利用队列的思维来遍历树
            while deposit:
                # 弹出对头元素进行判断
                head = deposit.pop(0)
                # 判断所在结点的右子结点是否为空，如果右子结点不为空则可以直接找下一组

                if head.left is None:
                    head.left = new
                    print('左子树添加了东西')
                    return
                elif head.right is None:
                    head.right = new
                    print('右子树添加了东西')
                    return
                # 如果本节点已满则开始找左子结点的
                else:
                    # 将本节点的左右子结点添加到队列中进行下一轮的寻找
                    deposit.append(head.left)
                    deposit.append(head.right)

遍历结点

树的遍历相较于线性表来说较为复杂，且不知一种方式。变量的主要方向为广度优先变量和深度优先变量其中广度优先变量的方式和我们上述添加结点的过程类似，但使用较少，深度优先中又分为先序遍历、中序遍历、后序遍历这三类。

1. 广度优先：按照层数，从左至右遍历。
2. 深度优先：
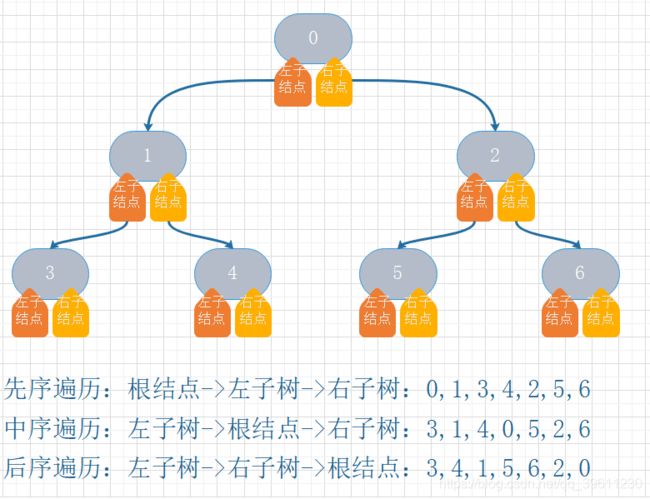
   1. 先序遍历：根结点->左子树->右子树，从根结点开始输出，之后优先输出左子树，最后输出右子树。
   2. 中序遍历：左子树->根结点->右子树，从左子树开始输出，之后输出根结点，同样最后输出右子树。
   3. 后序遍历：左子树->右子树->根结点：从左子树开始输出，之后输出右子树，最后输出根结点。
      三种遍历方式主要是根结点的输出位置有所变化。

广度优先

广度优先的代码我们在添加结点的基础上略微修改即可

    def wide(self):
        """广度优先遍历"""
        # 判断是否为空树，如果是空树则直接输出
        if self.__root is None:
            return '空树'
        else:
            # 用来存放(deposit)节点的数组
            deposit = [self.__root]
            # 利用队列的思维来遍历树
            while deposit:
                # 输出头元素
                head = deposit.pop(0)
                print(head.data, end=' ')

                if head.left is not None:
                    deposit.append(head.left)
                if head.right is not None:
                    deposit.append(head.right)

深度优先

    def before(self, root):
        """
        :param root: 传入头结点
        :return: 先序遍历
        """
        # 判断是否为空树，如果是空树则直接输出
        if root is None:
            return
        else:
            print(root.data, end=' ')
            self.before(root.left)
            self.before(root.right)

    def middle(self, root):
        """
        :param root: 传入头结点
        :return: 中序遍历
        """
        # 判断是否为空树，如果是空树则直接输出
        if root is None:
            return
        else:
            self.before(root.left)
            print(root.data, end=' ')
            self.before(root.right)

    def behind(self, root):
        """
        :param root: 传入头结点
        :return: 后序遍历
        """
        # 判断是否为空树，如果是空树则直接输出
        if root is None:
            return
        else:
            self.before(root.left)
            self.before(root.right)
            print(root.data, end=' ')